Тамара работает школьным психологом и отвечает за связь школы с родителями учеников. Она заметила, что одни родители (в основном матери) регулярно приходят в школу, интересуются успехами своих детей, встречаются с учителями, присутствуют на занятиях и т. п., а другие родители — крайне редкие гости в школе. Пытаясь понять, с какими факторами это связано, Тамара предположила, что одним из факторов, определяющих интерес родителей к школьным делам своих детей, является уровень их образования. Взяв список учеников школы (440 человек), она сформировала выборку из 44 человек (включив в выборку каждого десятого ученика) и узнала, сколько раз в течение учебного года их родители (матери) посетили школу. Из личного дела каждого ученика она узнала об уровне образования его матери. Затем Тамара составила таблицу (табл. 7.18), куда занесла сведения о числе посещений матерями школы в зависимости от уровня их образования [идея примера: Siegel, 1956].
Можно ли на основании полученных Тамарой данных утверждать, что число случаев посещения матерями школы зависит от уровня их образования?
Данная задача мало чем отличается от рассмотренных в предыдущих параграфах: несколько независимых выборок и результаты, представленные в шкале не ниже, чем шкала порядка. Без сомнений, здесь можно применить тест Крускала—Уоллиса или тест Джонкхиера—Терпстра, однако эти тесты не являются единственно возможными.
В подобных случаях используется также медианный тест для нескольких независимых выборок8. Он менее точен по сравнению с тестом Крускала— Уоллиса или Джонкхиера—Терпстра (там, где эти тесты выявляют различия медианный тест может их не обнаружить). Однако в тех случаях, когда нас особо беспокоит точность в принятии решений, медианный тест может оказаться более подходящим.
8 В своем первоначальном варианте медианный тест предназначался для случая двух независимых выборок, но затем он был расширен на число выборок больше двух [Siegel, 1956].
Таблица 7.18
Число посещений школы матерями в зависимости от уровня их образования
| Образование матери
| |||
| Незаконченное среднее | Среднее | Средне-специальное (техникум или колледж) | Высшее |
| 9 | 2 | 2 | 4 |
| 4 | 4 | 0 | 3 |
| 2 | 1 | 4 | 0 |
| 3 | 6 | 3 | 7 |
| 2 | 3 | 8 | 1 |
| 4 | 0 | 0 | 2 |
| 5 | 2 | 5 | 0 |
| 2 | 5 | 2 | 3 |
| 2 | 1 | 1 | 5 |
| 6 | 2 | 7 | 1 |
| 1 | 6 | ||
| 5 | |||
| 1 | |||
Как и во многих предыдущих случаях, проверка начинается с того, что все выборки объединяются. Затем вычисляется медиана объединенных значений, после чего каждое из значений сравнивается с медианой и подсчитывается, сколько из них больше медианы, а сколько меньше медианы или равно ей.
После проведенных вычислений исходная таблица с данными превращается в таблицу размером (2хk), где k — число независимых выборок, а число говорит о наличии в таблице двух категорий: «больше, чем медиана» и «равно медиане или меньше ее». Если различия между выборками носят случайный характер, столь же случайный характер будут носить различия между число» значений, которые больше, чем медиана, и числом значений, которые меньше чем медиана (или равны ей), для каждой из выборок.
Наличие различий для таблицы размером (2хk) проверяется с помог теста X2c (k – 1) числом степеней свободы.
Итак, выберем уровень значимости α =0,05 и сформулируем нулевую альтернативную гипотезы.
Н0: Матери, имеющие различный уровень образования, не отличаются друг от друга по числу посещений школы, в которой учатся их дети.
Н1: Матери, имеющие различный уровень образования, отличаются друг от друга по числу посещений школы, в которой учатся их дети (двусторонняя критическая область).
На первом этапе объединим все данные и вычислим медиану. Для этого составим таблицу (табл. 7.19), содержащую сведения о числе посещений, соответствующую им частоту, накопленную частоту и то, какой процент от выборки составляет данное значение накопленной частоты (см. параграф 1.1).
Из таблицы видно, что в качестве медианы можно использовать значение, равное двум посещениям (Ме=2), которое делит выборку пополам (накопленная частота равна 22, что соответствует 50% всех значений)9.
9 С учетом ряда обстоятельств, которые мы здесь не рассматриваем, точное значение медианы равно 2,5.
Таблица 7.19
Определение медианы
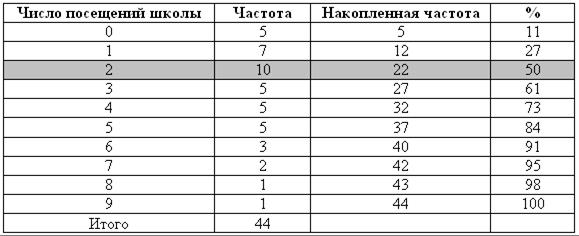
Определим для каждой выборки, сколько значений больше медианы (больше чем 2) и сколько меньше медианы или равно ей (табл. 7.20).
Таблица 7.20
Дата: 2018-12-21, просмотров: 765.