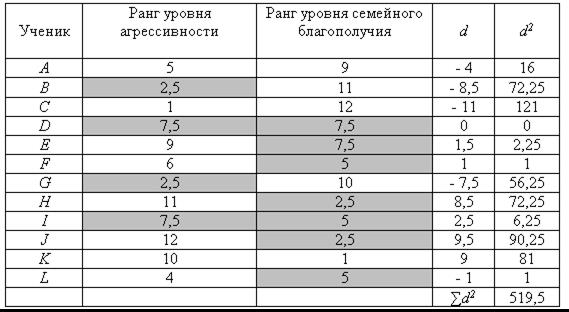
Как уже говорилось, при наличии связанных рангов обычной формулой для вычисления р пользоваться нельзя. Для этого случая необходимо использовать другую формулу, которая выглядит следующим образом:

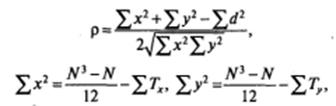
где 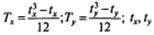— размер каждой группы связанных рангов (количество повторяющихся значений) для первого (х) и второго (у) столбцов; N — число пар коррелируемых значений. В нашем случае N=12.

В первом столбце (агрессивность) имеется две группы связанных рангов по два значения в каждой из групп: (2,5; 2,5) и (7,5; 7,5).

Во втором столбце (семейное благополучие) имеется три группы связанных рангов объемом в два, три и два значения: (2,5; 2,5), (5, 5, 5) и (7,5; 7,5).          

Найдем значения Т_х и Т_у:

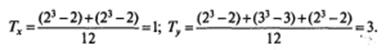
После всех пояснений приступим к вычислению р:

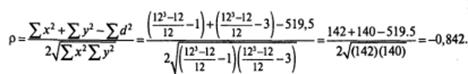
Между двумя показателями: уровнем агрессивности и уровнем семейного' | благополучия — получена отрицательная корреляционная связь.

Рассмотрим вторую возможность. Вычислим коэффициент ранговой кор­реляции Спирмена, игнорируя наличие связанных рангов.

В третьем случае вычисляется обычный коэффициент корреляции Пирсона, используемый в параметрической статистике⁵: r =−0,850.

⁵ Вследствие трудоемкости вычисления коэффициента корреляции Пирсона мы опускаем все промежуточные вычисления и приводим только конечный результат. Подробнее о вычисле­нии коэффициента корреляции Пирсона см., например: [Guilford, Fruchteг, 1977].

Подведем итоги.

В каждом из трех случаев были получены разные значения коэффициента корреляции. Наибольшее отклонение от истинного значения (р = − 0,842) бы­ло в случае игнорирования связанных рангов. Это наименее желанный ва­риант действий при использовании коэффициента ранговой корреляции Спирмена.

Поскольку ранговая корреляция по Спирмену уходит корнями в корреляцию по Пирсону6, между двумя значениями: р = − 0,842 и r = − 0,850 имеются незна­чительные различия. Поэтому в ряде случаев (если коррелируемые значения представлены в шкале интервалов или отношений) при наличии связанных рангов замена коэффициента ранговой корреляции Спирмена корреляцией по Пирсону, может быть оправданной. Но в любом случае предпочтительней ис­пользовать расчетную формулу, предназначенную для связанных рангов.

⁶ Коэффициент ранговой корреляции Спирмена можно рассматривать как частный случай коэффициента корреляции Пирсона. Поэтому между двумя коэффициентами существует взаи­мосвязь. Поскольку вычисление корреляции по Спирмену намного легче, чем вычисление кор­реляции по Пирсону, существуют специальные переводные таблицы, позволяющие вначале вычислить коэффициент ранговой корреляции Спирмена, а затем определить соответствующее значение коэффициента корреляции Пирсона.

Проверим полученное значение р = − 0,842 на значимость.

Выберем уровень значимости α =0,05 и сформулируем нулевую и альтерна­тивную гипотезы.

Н₀: Коэффициент корреляции между уровнем агрессивности учеников и уровнем их семейного благополучия равен нулю.

Н₁: Коэффициент корреляции между уровнем агрессивности учеников и уровнем их семейного благополучия меньше нуля (односторонняя критическая область).

Находим в табл. 11 (Приложение 2) для N = 12 и α=0,05 критическое значе­ние р =0,503. Поскольку эмпирическое значение |р| =0,842 больше, чем кри­тическое значение р =0,506, нулевая гипотеза отвергается. Существует значи­мая (на уровне α=0,05) отрицательная корреляционная связь между уровнем агрессивного поведения учеников и уровнем их семейного благополучия (чем более благополучна семья, тем менее агрессивно поведение ребенка).

ВКЛЮЧАЕМ КОМПЬЮТЕР...

Результаты оценивания фотографий представим в переменных «Шкала 1» (scale 1) и «Шкала 2» (scale 2). Дальнейшая последовательность действий и результат пока­заны на рис. 8.1—8.3.

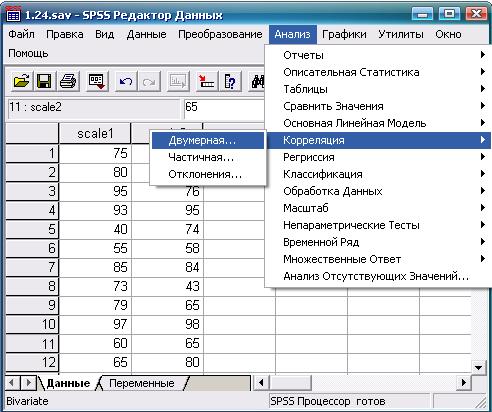
Рис. 8.1. Выбор требуемой статистической процедуры

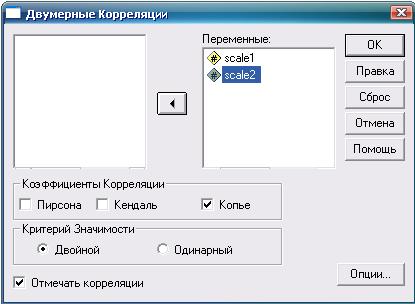
Рис. 8.2. Коэффициент ранговой корреляции Спирмена: необходимые действия и настройки

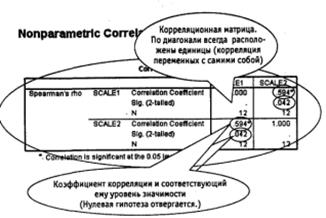
Рис. 8.3. Коэффициент ранговой корреляции Спирмена: результат

Приведем еще один результат (рис. 8.4) для случая связи между уровнем агрессив­ного поведения учеников и уровнем их семейного благополучия (случай связанных рангов). Для этого сведения об агрессивности учеников поместим в переменную «Агрессия» (aggress), а сведения об уровне семейного благополучия в переменную «Семейная ситуация» (situat).

Рис. 8.4. Коэффициент ранговой корреляции Спирмена: результат (случай связанных рангов)