| Уровень созависимости | |||||
| Сравнение первой выборки со второй и третьей | Низкий | Сравнение второй выборки с третьей | Средний | Высокий | |
| 3 | 1 | 55 | 1 | 58 | 52 |
| 0 | 0 | 75 | 0 | 65 | 38 |
| 2 | 1 | 60 | 4 | 45 | 35 |
| 1 | 1 | 63 | 4 | 40 | 64 |
| 4 | 2 | 50 | 1 | 62 | 47 |
| 4 | 43 | 48 | |||
| 1 | 53 | ||||
| U12=10 | U13=5 | U23=5 | |||
Найдем значение 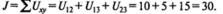
В том случае, если размеры сравниваемых выборок малы (не больше 8 значений в каждой), можно ограничиться полученным значением J и использовать таблицу критических значений для теста Джонкхиера-Терпстра, где, в зависимости от числа сравниваемых выборок и размера каждой из них, приведены критические значения J.
В общем случае, если предположить, что значения J имеют в популяции нормальный закон распределения, на основе сведений о выборках вычисляются среднее значение μJ и дисперсия σ2 J по следующим формулам:
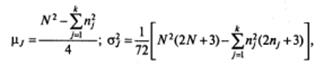
где N — общий объем (размер) выборки: 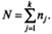
Подставим в формулы значения, соответствующие нашему случаю (k = 3; n1=5; n 2=7; n3 = 6; N=18)
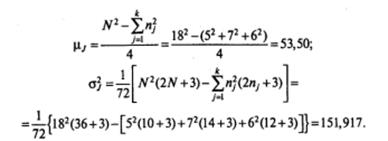
Стандартное отклонение σJ = √σ2 J =√151,911 =12,325.
На завершающем этапе вычисляется J *:
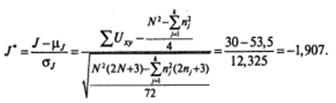
Нетрудно видеть, если что если J имеет нормальный закон распределения, то J* является аналогом г, что позволяет использовать таблицу z -распределения (табл. 1, Приложение 2).
Если найденному значению J* соответствует вероятность (для односторонней критической области) большая, чем значение уровня значимости а, у нас нет оснований отвергнуть нулевую гипотезу. Если соответствующая J* вероятность откажется меньшей или равной значению α, нулевая гипотеза отвергается и принимается альтернативная.
В таблице 1 (Приложение 2) для z-распределения находим, что значению z =−1,907 соответствует (приблизительно) вероятность р =0,0281. С учетом того, что альтернативная гипотеза сформулирована для двусторонней критической области, удваиваем полученное значение:
р =0,0562.
Поскольку значение вероятности р =0,0562 больше, чем выбранный уровень значимости α =0,05, у нас нет оснований отвергнуть нулевую гипотезу. Между тремя группами женщин, имеющими разный уровень созависимости, нет различий в показателе удовлетворенности браком.
Рассмотрим еще один пример.
Кристина работает социальным работником в дневном профилактории для подростков группы риска, употребляющих наркотики (преимущественно марихуану, гашиш и «экстази»). Из бесед с подростками она знает, в каком возрасте началось употребление, а также то, сколько правонарушений совершил подросток в течение года.
Сформировав гомогенную по возрасту группу из 16-летних подростков, Кристина узнала, сколько правонарушений в течение года совершил каждый из них. Она предположила, что на число совершаемых в течение года правонарушении влияет возраст начала употребления наркотиков: чем в более раннем возрасте началось употребление, тем большее число правонарушений в течений года было совершено.
Связав оба показателя (возраст начала употребления наркотиков и числе правонарушений в течение года), Кристина получила следующий результат (табл. 7.16).
Таблица 7.16
Дата: 2018-12-21, просмотров: 677.