| Уровень созависимости | ||
| Низкий | Средний | Высокий |
| 55 | 58 | 52 |
| 75 | 65 | 38 |
| 60 | 45 | 35 |
| 63 | 40 | 64 |
| 50 | 62 | 47 |
| 43 | 48 | |
| 53 | ||
Можно ли на основании полученных данных утверждать, что фактор созависимости влияет на степень удовлетворенности браком?
По сути дела, решаемая задача связана с выявлением значимых различий между результатами в трех сформированных группах. На первый взгляд она мало отличается от рассмотренного выше примера с тремя курсами психометрии, где использовался тест Крускала—Уоллиса. Однако можно увидеть, что в предыдущем примере фактор (курсы психометрии) был задан тремя ненаправленными альтернативами (курс психометрии А, курс психометрии В, курс психометрии С), и было не важно, в каком порядке следования этих альтернатив мы будем их сравнивать (полученный результат не изменится, если в таблице 7.6. курсы психометрии поменять местами).
Сейчас мы также имеем дело с тремя альтернативами (созависимость низкая, умеренная и высокая), но, в отличие от предыдущего примера, эти альтернативы носят направленный характер и образуют упорядоченную последовательность (от меньшего значения к большему), что можно учесть в процессе обработки полученных результатов.
В том случае, когда независимые выборки можно расположить в определенном порядке, соответствующем упорядоченным градациям какого-либо фактора, для их сравнения обычно применяется тест Джонкхиера—Терпстра5 для упорядоченных альтернатив.
5 Оба автора, независимо друг от друга и практически одновременно описали подход, используемый в данном тесте. В ряде публикаций на русском языке он упоминается как тест Джонкира— Терпстра или тест Джонкхира.
Например, в ходе одного из исследований по безопасности движения было сформировано несколько выборок добровольцев, подвергшихся воздействию возрастающих от выборки к выборке доз алкоголя. В каждой выборке измерялись скорость реакции, объем восприятия и другие показатели, влияющие на безопасность дорожного движения, и проводилось сравнение результатов в выборках между собой. В подобных ситуациях тест Джонкхиера—Терпстра позволяет не только сравнивать выборки между собой, но и обнаруживать в получаемых результатах определенные тенденции (тренды), являющиеся следствием действия какого-либо упорядоченного по своим градациям фактора (например, возрастающих доз алкоголя).
Используемый в тесте Джонкхиера—Терпстра подход представляет собой развитие идей, лежащих в основе теста Манна—Уитни.
Основой для принятия решения о существовании различий между результатами в k; независимых и расположенных в определенном порядке выборках является вычисляемое значение J (см. ниже) или величина J*, вычисляемая по следующей общей формуле:
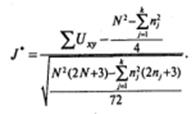
Для понимания смысла содержащихся в формуле обозначений приступим к сравнению выборок.
Выберем уровень значимости α =0,05 и сформулируем нулевую и альтернативную гипотезы.
Н0: Между тремя группами женщин, имеющими разный уровень созависимости, нет различий в показателе удовлетворенности браком.
Н1: Между тремя группами женщин, имеющими разный уровень созависимости, существуют различия в показателе удовлетворенности браком (двусторонняя критическая область).
Процесс проверки сформулированных гипотез включает ряд этапов.
Вначале все k выборок попарно сравниваются друг с другом в направлении, заданном фактором. Для случая трех выборок (k = 3) первая выборка сравнивается со второй, затем первая выборка сравнивается с третьей, затем вторая выборка сравнивается с третьей.
Процесс сравнения происходит в соответствии с той процедурой, которая была описана выше для теста Манна—Уитни (параграф 6.3).
В результате каждого сравнения определяется, сколько значений во второй из двух сравниваемых выборок больше каждого из значений в первой из них. Например, если сравнить первую выборку со второй (табл. 7.13), то для первого значения в первой выборке (55) во второй выборке можно найти три значения (58, 65, 62), превышающие 55. Результат сравнения для значения 55 будет равен трем. Если перейти ко второму значению в первой выборке (75), то во второй выборке нет ни одного значения, большего, чем 75. Результат сравнений будет равен нулю.
По результатам каждого сравнения выборок находится сумма полученных результатов, обозначенная в формуле как Uxy6 (табл. 7.15).
6 Если последовательно применить тест Манна—Уитни для трех пар сравниваемых выборок (первая и вторая, первая и третья, вторая и третья) и в каждом случае найти значения U (см. параграф 6.3), мы получим тот же результат.
Таблица 7.15
Дата: 2018-12-21, просмотров: 674.