| Оценка | 690 | 691 | 692 | 695 | 697 | 700 | 705 | 710 | 712 | 715 | 720 | 722 | 727 | 732 |
| Ранг | 1 | 2 | 3 | 4 | 5 | 6 | 7' | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
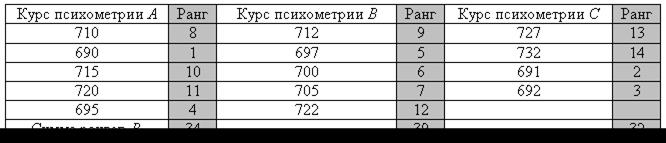
Дополним таблицу 7.7 значениями рангов для каждой выборки и найдем их сумму. Получим модифицированную таблицу 7.9.
Приступим к вычислению Н для случая k = 3, n1 = 5, n2 = 5, n3=4, N=14, R1=34, R2=39, R3 =32.
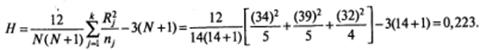
4 Данный тест позволяет выявить различия между выборками, но не направление этих различий. С его помощью нельзя определить, в какой из трех выборок наилучшие результаты. Для ответа на данный вопрос необходимо попарно сравнивать выборки между собой, например, с помощью теста Манна—Уитни.
Таблица 7.9
Результаты психометрии и их ранги
Для случая k =3, 2 ≤ n1, n 2, n3 ≤ 5 существует специальная статистическая таблица для теста Крускала—Уоллиса, в которой найденное значение Нэмпир сравнивается с критическим значением Нкритич.
В общем случае (при любых значениях k и N используется статистическая таблица критических значений для теста Х2с(k — 1) числом степеней свободы (табл. 2, Приложение 2). Если значение Х2критич оказывается больше вычисленного значения Нэмпир, нет оснований отвергнуть нулевую гипотезу. Если значение Х2критич оказывается меньше вычисленного значения Нэмпир или равно ему,
нулевая гипотеза отклоняется и принимается альтернативная.
Найдем по таблице 2 значение Х2критич для df = ( k —1) = (3 — 1) = 2 и α =0,05: Х2критич = 5,99. Поскольку это значение больше, чем Нэмпир =0,223, нет оснований отвергнуть нулевую гипотезу. Между результатами психометрического экзамена у выпускников курсов А, В и С нет различий.
В рассмотренном примере выборки не содержали повторяющихся (одинаковых) значений. В том случае, если имеются повторяющиеся значения, для вычисления Н используется скорректированная формула, учитывающая факт наличия связанных рангов.
Рассмотрим еще один пример применения теста Крускала—Уоллиса для случая связанных рангов.
Таблица 7.10
Возраст начала курения
| Коренные израильтяне (евреи) | Израильтяне — бедуины | Иммигранты из б. СССР | Иммигранты из Эфиопии |
| 10 | 7 | 9 | 13 |
| 12 | 6 | 7 | 10 |
| 11 | 8 | 12 | 11 |
| 12 | 10 | 11 | 14 |
| 10 | 11 | 6 | 12 |
| 13 | 9 | 13 | 11 |
| 13 | 12 | 10 | 13 |
Из курящих подростков, представляющих коренных израильтян-евреев, израильтян-бедуинов, иммигрантов из бывшего СССР и иммигрантов из Эфиопии были сформированы четыре независимые выборки. В таблице 7.10 приведены сведения о возрасте начала курения для каждой из выборок.
Можно ли утверждать, что подростки, принадлежащие к различным культурно-этническим группам, начинают курить в разном возрасте?
Поскольку алгоритм дальнейших действий нам уже известен, сразу приступаем к использованию теста Крускала—Уоллиса.
Выберем уровень значимости α =0,05 и сформулируем нулевую и альтернативную гипотезы.
Н0: Нет отличий в возрасте начала курения у израильских подростков — представителей различных этнокультурных групп.
Н1: Израильские подростки — представители различных этнокультурных групп начинают курить в различном возрасте (двусторонняя критическая область).
Как и в предыдущем примере, объединим все выборки в одну, запишем содержащиеся в выборках значения в порядке возрастания и проранжируем их (табл. 7.11).
Таблица 7.11
Дата: 2018-12-21, просмотров: 694.