Вычетом функции  в изолированной особой точке
в изолированной особой точке  называется число, обозначаемое символом
называется число, обозначаемое символом 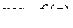 или
или 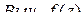 и определяемое равенством
и определяемое равенством 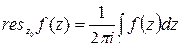 . Здесь
. Здесь 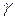 – произвольный контур, на котором функция
– произвольный контур, на котором функция  аналитическая, а в области, ограниченной этим контуром, нет других особых точек функции
аналитическая, а в области, ограниченной этим контуром, нет других особых точек функции  , кроме
, кроме  .
.
Способы вычисления вычетов.
1. Для любого типа особой точки  вычет равен коэффициенту при минус первой степени в разложении функции
вычет равен коэффициенту при минус первой степени в разложении функции  в ряд Лорана по степеням
в ряд Лорана по степеням 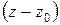 , то есть
, то есть 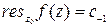
2. Вычет в устранимой особой точке равен нулю.
3. Вычет в полюсе порядка 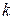 находится по формуле
находится по формуле
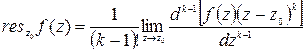 .
.
В частности в простом полюсе (первого порядка) формула принимает вид
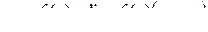 .
.
Если  может быть представлена в виде
может быть представлена в виде 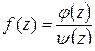 , где
, где  ,
,
 ,
,  , то
, то 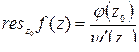 .
.
Основная теорема Коши о вычетах. если функция  аналитична на границе
аналитична на границе  области
области 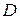 и всюду внутри этой области, за исключением конечного числа особых точек
и всюду внутри этой области, за исключением конечного числа особых точек 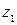 ,
,  , ... ,
, ... ,  то
то
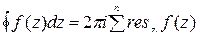 .
.
Задача 6.1
Вычислить интеграл, используя основную теорему Коши о вычетах:
a) 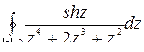 ; б)
; б) 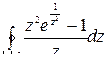 .
.
Решение
а) функция 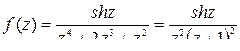 имеет две изолированные особые точки
имеет две изолированные особые точки 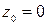 и
и 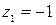 . Причем обе лежат внутри контура интегрирования.
. Причем обе лежат внутри контура интегрирования.
Для точки 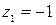 представим подынтегральную функцию
представим подынтегральную функцию  в виде:
в виде: 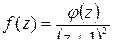 , где
, где 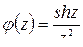 аналитическая в точке
аналитическая в точке 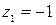 , причём
, причём 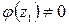 . Применяя теорему 2´ для определения типа изолированной особой точки, заключаем что
. Применяя теорему 2´ для определения типа изолированной особой точки, заключаем что 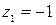 полюс второго порядка. Используем третий способ вычисления вычета в полюсе порядка
полюс второго порядка. Используем третий способ вычисления вычета в полюсе порядка 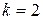 :
:
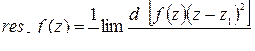 =
= 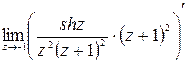 =
= 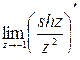 =
=
= 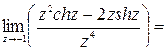
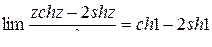 .
.
Для точки 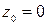 функции
функции 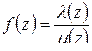 , где
, где 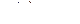 , а
, а  применим теорему 2" для определения её типа.
применим теорему 2" для определения её типа.
 ,
, 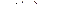 ,
,  ,
,
следовательно, 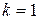 .
.
 ,
, 
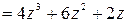 ,
,  ,
, 
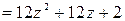 ,
,
следовательно 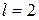 .
.
Тогда  полюс порядка
полюс порядка 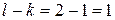 . Изолированная особая точка
. Изолированная особая точка  является полюсом первого порядка или простым полюсом. Используем третий способ вычисления вычета в простом полюсе:
является полюсом первого порядка или простым полюсом. Используем третий способ вычисления вычета в простом полюсе:
 =
= 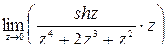 =
= 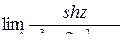 =
=
= 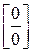 =(по правилу Лопиталя)=
=(по правилу Лопиталя)= 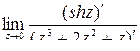 =
= 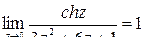
По теореме Коши о вычетах имеем:
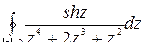 =
= 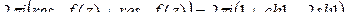 .
.
б) подынтегральная функция 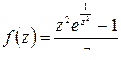 внутри контура интегри-рования
внутри контура интегри-рования 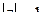 имеет единственную изолированную особую точку
имеет единственную изолированную особую точку 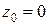 . По теореме Коши о вычетах
. По теореме Коши о вычетах
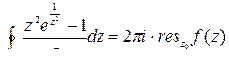 .
.
Применим первый способ вычисления вычета 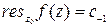 , для чего разложим функцию
, для чего разложим функцию 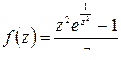 в ряд Лорана по степеням
в ряд Лорана по степеням 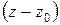 , используя известное разложение
, используя известное разложение
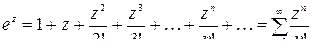 .
.
Имеем:
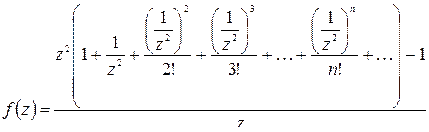 =
=
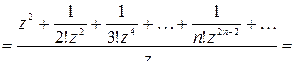
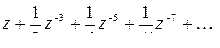
Замечаем что в полученном разложении отсутствует член с 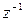 , то есть коэффициент при минус первой степени
, то есть коэффициент при минус первой степени 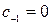 . Таким образом,
. Таким образом,

и значит, 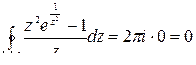 .
.
Расчетное задание
| Задача 1. Вычислить | |||
| 1.1 | 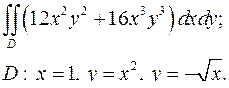
| 1.2 | 
|
| 1.3. | 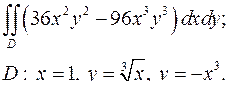
| 1.4. | 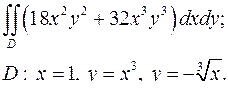
|
| 1.5. | 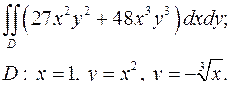
| 1.6. | 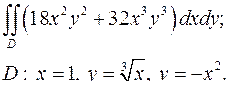
|
| 1.7. | 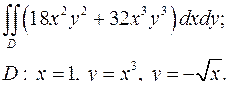
| 1.8. | 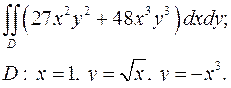
|
| 1.9. | 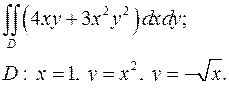
| 1.10. | 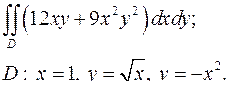
|
| 1.11. | 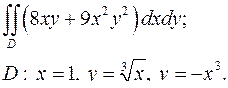
| 1.12. | 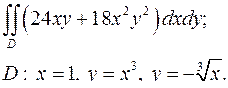
|
| 1.13. | 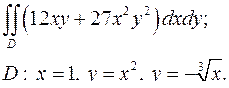
| 1.14. | 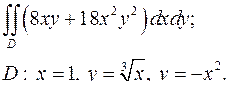
|
| 1.15. | 
| 1.16. | 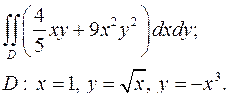
|
| 1.17. | 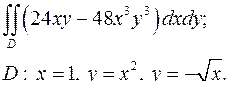
| 1.18. | 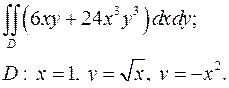
|
| Задача 1. Вычислить | |||
| 1.19. | 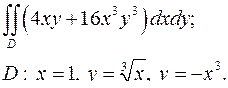
| 1.20. | 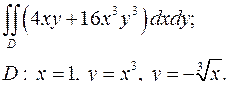
|
| 1.21. | 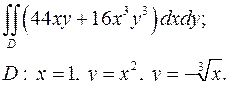
| 1.22. | 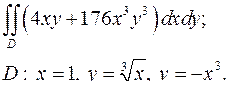
|
| 1.23. | 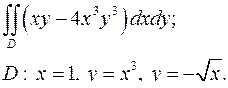
| 1.24. | 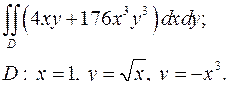
|
| 1.25. | 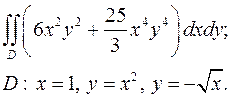
| 1.26. | 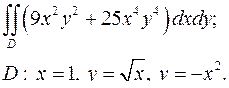
|
| 1.27. | 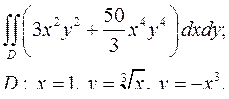
| 1.28. | 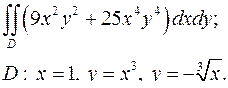
|
| 1.29. | 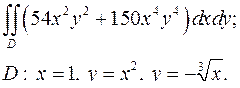
| 1.30. | 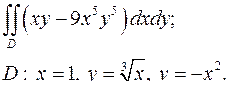
|
| 1.31. | 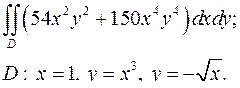
| ||
| Задача 2. Найти объем тела, заданного ограничивающи-ми его поверхностями | |||
| 2.1. | 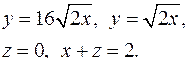
| 2.2. | 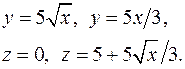
|
| 2.3. | 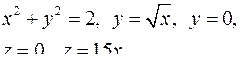
| 2.4. | 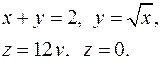
|
| 2.5. | 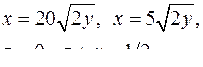
| 2.6. | 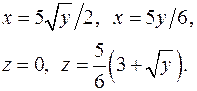
|
| 2.7. | 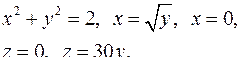
| 2.8. | 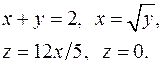
|
| 2.9. | 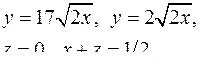
| 2.10. | 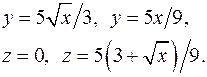
|
| 2.11. | 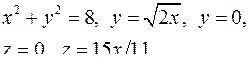
| 2.12. | 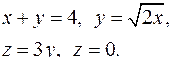
|
| 2.13. | 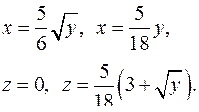
| 2.14. | 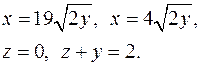
|
| 2.15. | 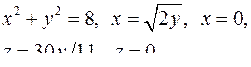
| 2.16. | 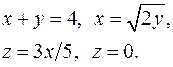
|
| 2.17. | 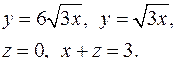
| 2.18. | 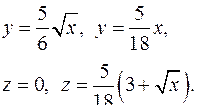
|
| 2.19. | 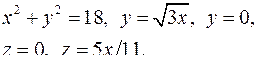
| 2.20. | 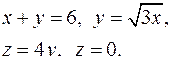
|
| Задача 2. Найти объем тела, заданного ограничивающи-ми его поверхностями | |||
| 2.21. | 
| 2.22. | 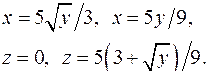
|
| 2.23. | 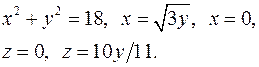
| 2.24. | 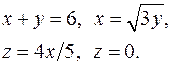
|
| 2.25. | 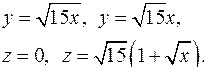
| 2.26. | 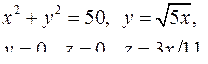
|
| 2.27. | 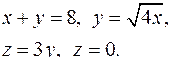
| 2.28. | 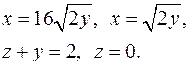
|
| 2.29. | 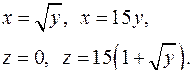
| 2.30. | 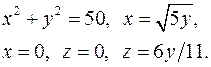
|
| 2.31. | 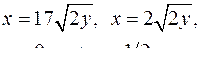
| ||
| Задача 3. Найти производную скалярного поля | |
| 3.1. | 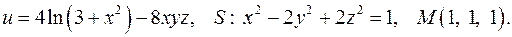
|
| 3.2. | 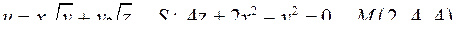
|
| 3.3. | 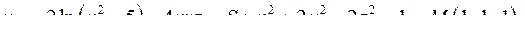
|
| 3.4. | 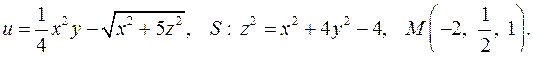
|
| 3.5. | 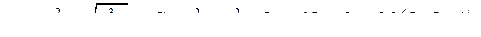
|
| 3.6. | 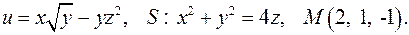
|
| 3.7. | 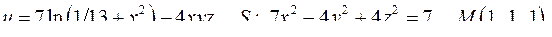
|
| 3.8. | 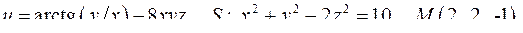
|
| 3.9. | 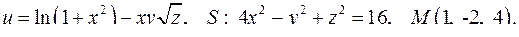
|
| 3.10. | 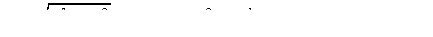
|
| 3.11. | 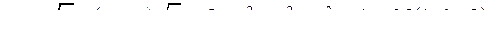
|
| 3.12. | 
|
| 3.13. | 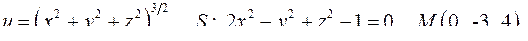
|
| 3.14. | 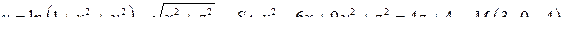
|
| Задача 3. Найти производную скалярного поля | |||
| 3.15. | 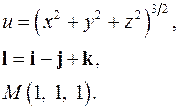
| 3.16. | 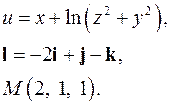
|
| 3.17. | 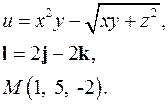
| 3.18. | 
|
| 3.19. | 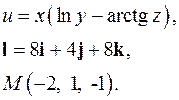
| 3.20. | 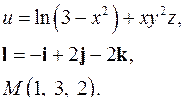
|
| 3.21. | 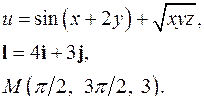
| 3.22. | 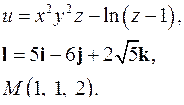
|
| 3.23. | 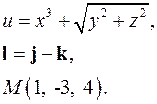
| 3.24. | 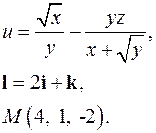
|
| 3.25. | 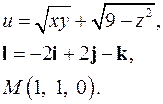
| 3.26. | 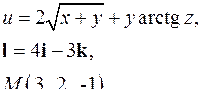
|
| 3.27. | 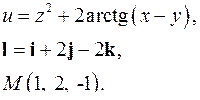
| 3.28. | 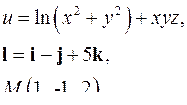
|
| 3.29. | 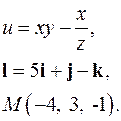
| 3.30. | 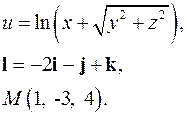
|
| 3.31. | 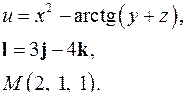
| ||
| Задача 4. Найти угол между градиентами скалярных полей | |
| 4.1. | 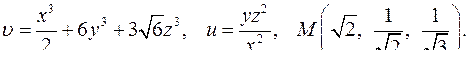
|
| 4.2. | 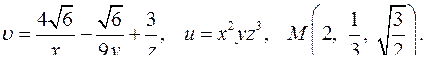
|
| 4.3. | 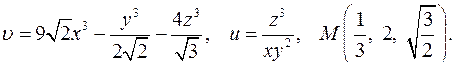
|
| 4.4. | 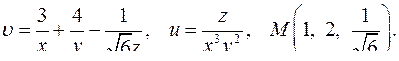
|
| 4.5. | 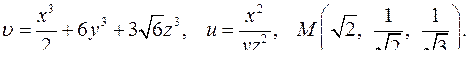
|
| 4.6. | 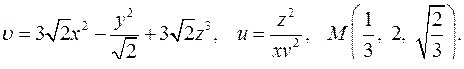
|
| 4.7. | 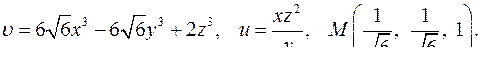
|
| 4.8. | 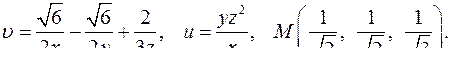
|
| 4.9. | 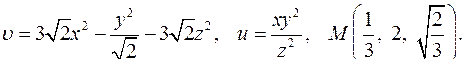
|
| 4.10. | 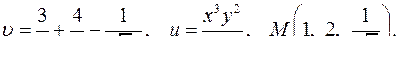
|
| 4.11. | 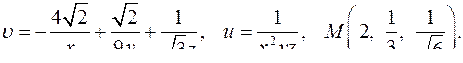
|
| 4.12. | 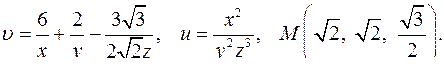
|
| 4.13 . | 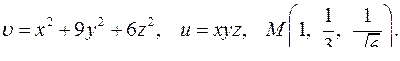
|
| Задача 4. Найти угол между градиентами скалярных полей | |
| 4.14. | 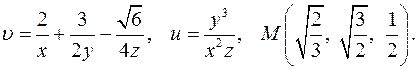
|
| 4.15. | 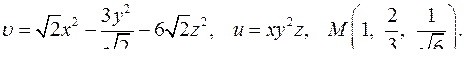
|
| 4.16. | 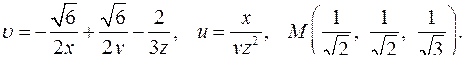
|
| 4.17. | 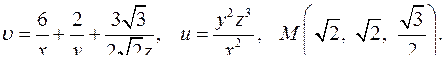
|
| 4.18. | 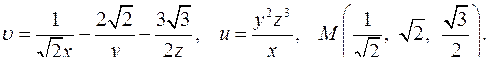
|
| 4.19. | 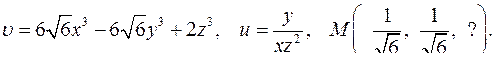
|
| 4.20. | 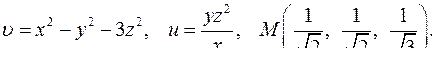
|
| 4.21. | 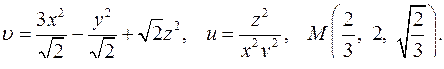
|
| 4.22. | 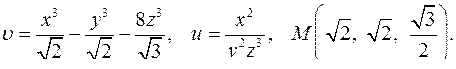
|
| 4.23. | 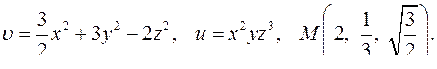
|
| 4.24. | 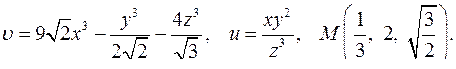
|
| 4.25. | 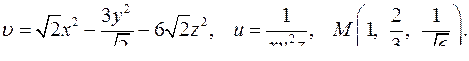
|
| 4.26. | 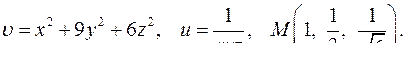
|
| Задача 4. Найти угол между градиентами скалярных полей | |
| 4.27. | 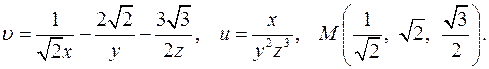
|
| 4.28. | 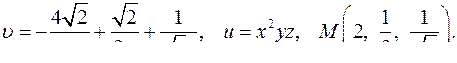
|
| 4.29. | 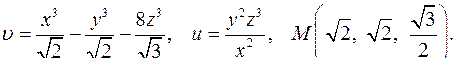
|
| 4.30. | 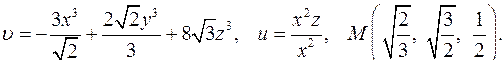
|
| 4.31. | 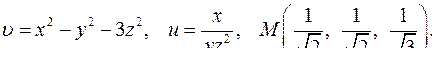
|
| Задача 5. Найти поток векторного поля | |||
| 5.1. | 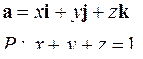
| 5.2. | 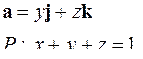
|
| 5.3. | 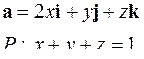
| 5.4. | 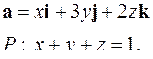
|
| 5.5. | 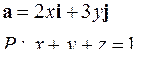
| 5.6. | 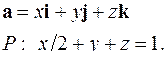
|
| 5.7. | 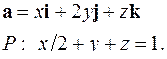
| 5.8. | 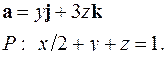
|
| 5.9. | 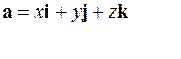
| 5.10. | 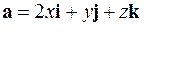
|
| 5.11. | 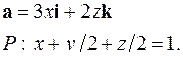
| 5.12. | 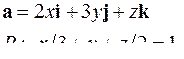
|
| 5.13. | 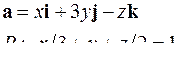
| 5.14. | 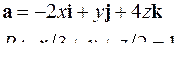
|
| Задача 5. Найти поток векторного поля | |||
| 5.15. | 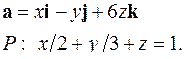
| 5.16. | 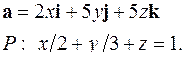
|
| 5.17. | 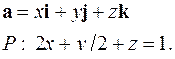
| 5.18. | 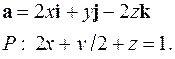
|
| 5.19. | 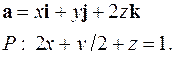
| 5.20. | 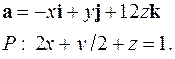
|
| 5.21. | 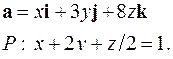
| 5.22. | 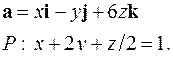
|
| 5.23. | 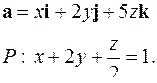
| 5.24. | 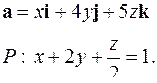
|
| 5.25. | 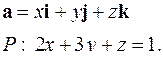
| 5.26. | 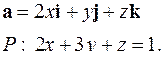
|
| 5.27. | 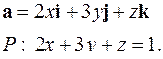
| 5.28. | 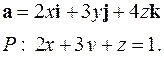
|
| 5.29. | 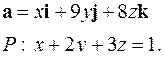
| 5.30. | 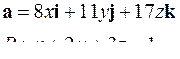
|
| 5.31. | 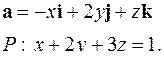
| ||
| Задача 7. Найти все значения корней | |||||
| 7.1. |
а) 
|  б)
б) 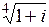
|  7.2.
7.2.
|
а) 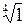
| б) 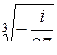
|
| 7.3. | а) 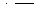
| б) 
| 7.4. | а) 
| б) 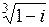
|
| 7.5. | а) 
| б) 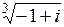
| 7.6. | а) 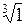
| б) 
|
| 7.7. | а) 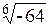
| б) 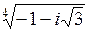
| 7.8. | а) 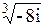
| б) 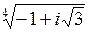
|
| 7.9. | а) 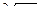
| б) 
| 7.10. | а) 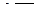
| б) 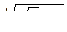
|
| 7.11. | а) 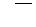  
| б) 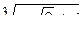
| 7.12. | а) 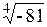
| б) 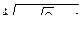
|
| 7.13. | а) 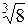
| б) 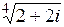
| 7.14. | а) 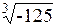
| б) 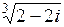
|
| 7.15. | а) 
| б) 
| 7.16. | а) 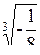
| б) 
|
| 7.17. | а) 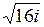
| б) 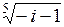
| 7.18. | а) 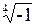
| б) 
|
| 7.19. | а) 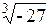
| б) 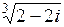
| 7.20. | а) 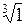
| б) 
|
| 7.21. | а) 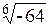
| б) 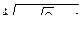
| 7.22. | а) 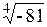
| б) 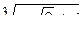
|
| 7.23. | а) 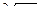
| б) 
| 7.24. | а) 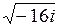
| б) 
|
| 7.25. | а) 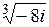
| б) 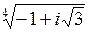
| 7.26. | а) 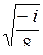
| б) 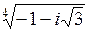
|
| 7.27. | а) 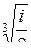 ; ;  
| б) 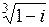
| 7.28. | а) 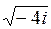 ; ;
| б) 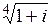
|
| 7.29. | а) 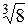 ; ;
| б) 
| 7.30. | а) 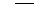 ; ;
| б) 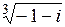
|
| Задача 8. Восстановить аналитическую в окрестности точки | |||
| 8.1. | 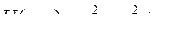 , , 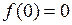
| 8.2. | 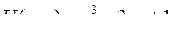 , , 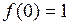
|
| 8.3. |  , , 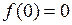
| 8.4. | 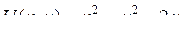 , , 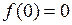
|
| 8.5. | 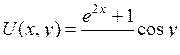 , , 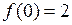
| 8.6. | 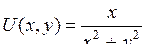 , , 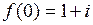
|
| 8.7. | 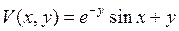 , , 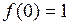
| 8.8. |  , , 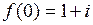
|
| 8.9. |  , f(0)=1 , f(0)=1
| 8.10. | 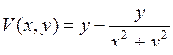 , , 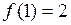
|
| 8.11. | 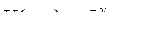 , , 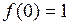
| 8.12. | 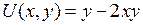 , , 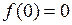
|
| 8.13. | 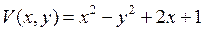 , , 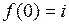
| 8.14. | 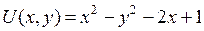 , , 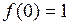
|
| 8.15. | 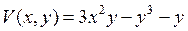 , , 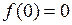
| 8.16. | 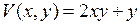 , , 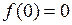
|
| 8.17. |  , , 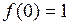
| 8.18. | 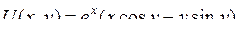 , , 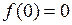
|
| 8.19. | 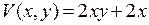 , , 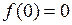
| 8.20. | 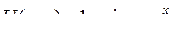 , , 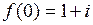
|
| 8.21. | 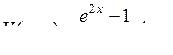 , , 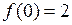
| 8.22. | 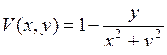 , , 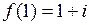
|
| 8.23. | 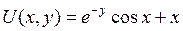 , , 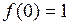
| 8.24. | 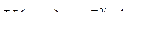 , , 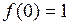
|
| 8.25. | 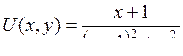 , , 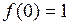
| 8.26. | 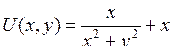 , f(1)=2 , f(1)=2
|
| 8.27. | 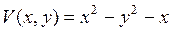 , , 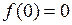
| 8.28. |  , , 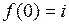
|
| 8.29. | 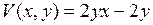 , , 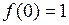
| 8.30. | 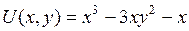 , , 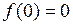
|
Задача 9. Определить типы изолированных особых точек функции
9.1. а) 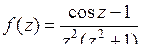 б)
б) 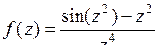
9.2. а) 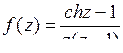 ; б)
; б) 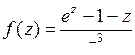
9.3. а) 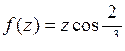 ; б)
; б) 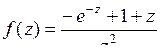
9.4. а) 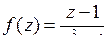 ; б)
; б) 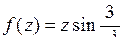
9.5. а) 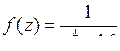 ; б)
; б) 
9.6. а)  ; б)
; б) 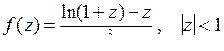
9.7. а) 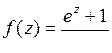 ; б)
; б) 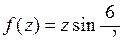
9.8. а) 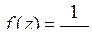 ; б)
; б) 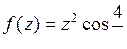
9.9. а) 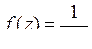 ; б)
; б) 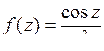
9.10. а) 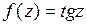 ; б)
; б) 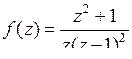
9.11. а) 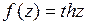 ; б)
; б) 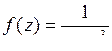
9.12. а) 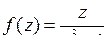 ; б)
; б) 
9.13. а) 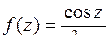 ; б)
; б) 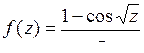
9.14. а) 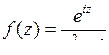 ; б)
; б) 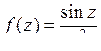
9.15. а) 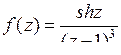 ; б)
; б) 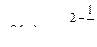
9.16. а) 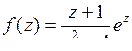 ; б)
; б) 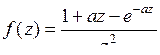
9.17. а) 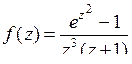 ; б)
; б) 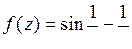
9.18. а) 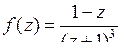 ; б)
; б) 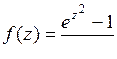
9.19. а) 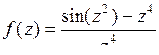 ; б)
; б) 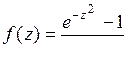
9.20. а) 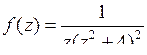 ; б)
; б) 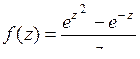
9.21. а) 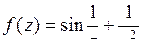 ; б)
; б) 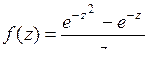
9.22. а) 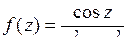 ; б)
; б) 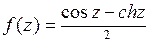
9.23. а) 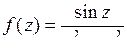 ; б)
; б) 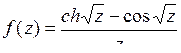
9.24. а) 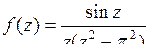 ; б)
; б) 
9.25. а) 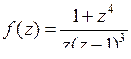 ; б)
; б) 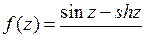
9.26. а) 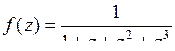 ; б)
; б) 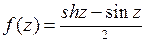
9.27. а) 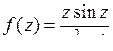 ; б)
; б) 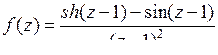
9.28. а) 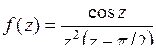 ; б)
; б) 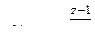
9.29. а) 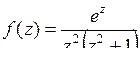 ; б)
; б) 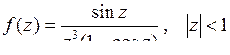
9.30. а) 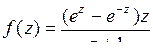 ; б)
; б) 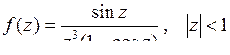
Задача 10. Вычислить интегралы от функции комплексного переменного
10.1. а) 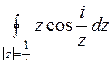 ; б)
; б) 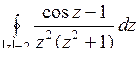
10.2. а) 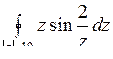 ; б)
; б) 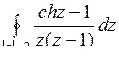
10.3. а) 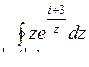 ; б)
; б) 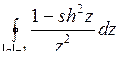
10.4. а) 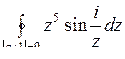 ; б)
; б) 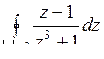
10.5. а) 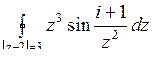 ; б)
; б) 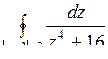
10.6. а) 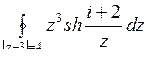 ; б)
; б) 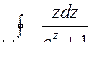
10.7. а) 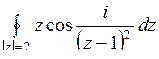 ; б)
; б) 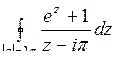
10.8. а) 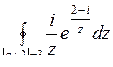 ; б)
; б) 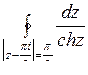
10.9. а) 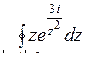 ; б)
; б) 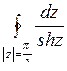
10.10. а) 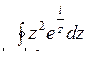 ; б)
; б) 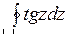
10.11. а) 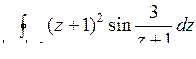 ; б)
; б) 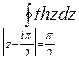
10.12. а) 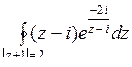 ; б)
; б) 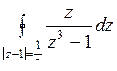
10.13. а) 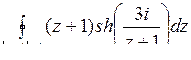 ; б)
; б) 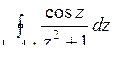
10.14. а) 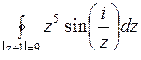 ; б)
; б) 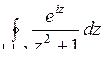
10.15. а) 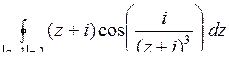 ; б)
; б) 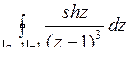
10.16. а) 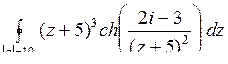 ; б)
; б) 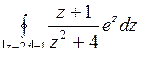
10.17. а) 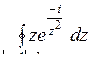 ; б)
; б) 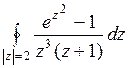
10.18. а) 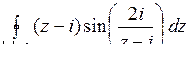 ; б)
; б) 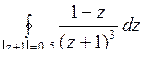
10.19. а) 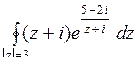 ; б)
; б) 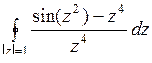
10.20. а) 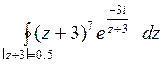 ; б)
; б) 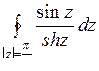
10.21. а) 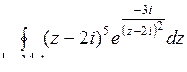 ; б)
; б) 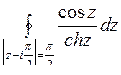
10.22. а) 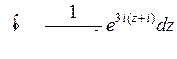 ; б)
; б) 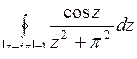
10.23. а) 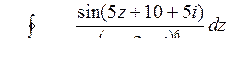 ; б)
; б) 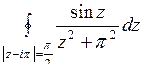
10.24. а) 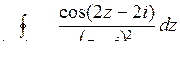 ; б)
; б) 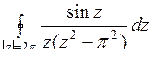
10.25. а) 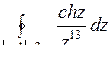 ; б)
; б) 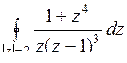
10.26. а) 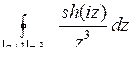 ; б)
; б) 
10.27. а) 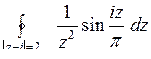 ; б)
; б) 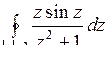
10.28. а) 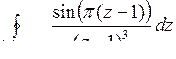 ; б)
; б) 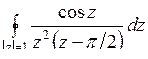
10.29. а) 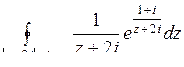 ; б)
; б) 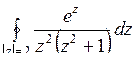
10.30. а) 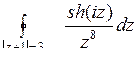 ; б)
; б) 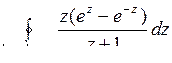
СОДЕРЖАНИЕ
| Введение ……………………………………………………………………………………………………………………………..…......… | 3 |
| Рекомендации по изучению теоретического материала ………………………………………………… | 4 |
| 1. Кратные интегралы | 5 |
| 1.1. Задача об объеме цилиндрического бруса ………………………………..……….……. | 5 |
| 1.2. Определение двойного интеграла ……………………………………………….…………... | 6 |
| 1.3. Свойства двойного интеграла ……………………………………………………………………. | 7 |
| 1.4. Сведение двойного интеграла к повторному интегралу ……………………..….. | 8 |
| 1.5. Вычисление двойных интегралов ………………………………………………………...….. | 11 |
| 1.5.1. Вычисление двойных интегралов в декартовых координатах ……… | 11 |
| 1.5.2. Замена переменных в двойных интегралах ………………………………………. | 15 |
| 1.6. Приложения двойных интегралов к геометрии и механике ………………….…. | 23 |
| 1.6.1. Вычисление площадей плоских фигур ……………………………………….…... | 23 |
| 1.6.2. Вычисление объемов тел …………………………………………………………….….. | 25 |
| 1.6.3. Вычисление площадей поверхностей ………………………………………….... | 29 |
| 1.6.4. Некоторые приложения двойных интегралов к механике ……………………. | 32 |
| 1.7. Задача о вычислении массы тела ……………………………………………………………. | 35 |
| 1.8. Определение тройного интеграла ……………………………………………..……………… | 36 |
| 1.9. Свойства тройного интеграла ……………………………………………………………………. | 37 |
| 1.10. Вычисление тройных интегралов …………………………………………………………… | 38 |
| 1.10.1. Вычисление тройных интегралов в декартовых координатах ……………. | 38 |
| 1.10.2. Замена переменных в тройных интегралах …………………………………. | 42 |
| 1.11. Приложения тройных интегралов ……………………………………………………..…… | 45 |
| 2. Теория поля | 57 |
| 2.1. Скалярное поле. Производная по направлению. Градиент ……………..……… | 57 |
| 2.2. Векторное поле. Векторные линии ………………………………….………………………. | 60 |
| 2.3. Поток векторного поля ……………………………………………………………..………………. | 62 |
| 2.4. Дивергенция. Формула Остроградского-Гаусса …………………………….…………. | 66 |
| 2.5. Линейный интеграл и циркуляция ……………………………………………………….….. | 69 |
| 2.6. Ротор. Формула Стокса …………………………………………………………………………….. | 71 |
| 3. Теория функций комплексного переменного | 75 |
| 3.1. Комплексные числа и действия над ними ……………………………………………… | 75 |
| 3.2. Функции комплексного переменного …………………………………………………….. | 81 |
| 3.3. Интеграл в комплексной области. Интегральная формула Коши …………... | 85 |
| 3.4. Степенной ряд в комплексной области. Ряд Тейлора ……………………………. | 89 |
| 3.5. Ряд Лорана. Классификация особых точек …………………………………………….. | 91 |
| 3.6. Вычеты. Вычисление интегралов с помощью вычетов ……………………………. | 97 |
| РАСЧЕТНОЕ ЗАДАНИЕ (задачи 1-10) ….………………………………………………………………… | 100 |
Учебно-практическое издание
МАТЕМАТИКА
Учебный практикум и контрольные задания
3 семестр
Для студентов заочной формы обучения
Составители
Бобков Владимир Иванович
Борисов Андрей Валерьевич
Зуев Михаил Федорович
Технический редактор М.А. Андреев
Корректор Л.И. Чурлина
_____________________________________________________________________________________________
Темплан издания филиала МЭИ в г. Смоленске, учебно-практ.
Подписано в печать 11.04.2012 г.
Формат бумаги 60×84 1/16. Тираж 50 экз. Печ. л. 7,4. Усл. печ. л. 6,86.
_____________________________________________________________________________________________
Издательский сектор филиала МЭИ в г. Смоленске
214013 г. Смоленск, Энергетический проезд, 1
[1] Символ «!!» означает факториал по четным.
Дата: 2018-12-21, просмотров: 409.
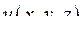 в точке
в точке 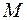 по направлению нормали к поверхности
по направлению нормали к поверхности 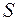 , образующей острый угол с положительным направлением оси
, образующей острый угол с положительным направлением оси 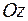
 и
и 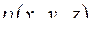 в точке
в точке 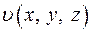 в точке
в точке 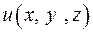 и
и 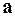 через часть плоскости
через часть плоскости 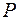 ,
,  функцию
функцию 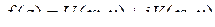 по известной действительной
по известной действительной 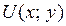 или мнимой
или мнимой 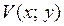 части и значению
части и значению 