Пусть в области D заданы непрерывная функция
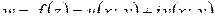
и гладкая кривая  с началом в точке A и концом в точке B, заданная уравнением
с началом в точке A и концом в точке B, заданная уравнением  ,
, 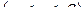 или, что всё равно, двумя уравнениями:
или, что всё равно, двумя уравнениями: 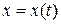 и
и 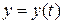 ,
, 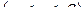 .
.
Как обычно, направление на  соответствует изменению параметра
соответствует изменению параметра 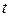 от
от 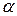 до
до 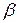 , то есть
, то есть 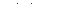 и
и 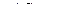 . Интеграл от функции
. Интеграл от функции 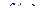 по кривой
по кривой  определяется как:
определяется как:
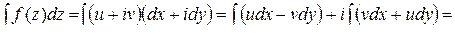
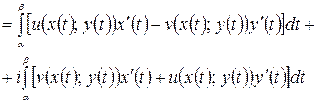 (3.2)
(3.2)
Из (3.2) видно, что интеграл по комплексному переменному есть сумма двух криволинейных интегралов, и его вычисление сводится к вычислению обыкновенных интегралов.
Если кривая L кусочно-гладкая и состоит из гладких ориентированных кусков L1, L2, ..., Ln, то по определению считаем, что 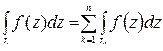 .
.
 Теорема Коши (для односвязной области) . Если функция f(z) аналитична в односвязной области D, ограниченной замкнутым кусочно-гладким контуром Г, и непрерывна в
Теорема Коши (для односвязной области) . Если функция f(z) аналитична в односвязной области D, ограниченной замкнутым кусочно-гладким контуром Г, и непрерывна в  , то
, то 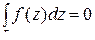 .
.
 Теорема Коши (для многосвязной области). Если функция f(z) аналитична в многосвязной области D, ограниченной замкнутыми кусочно-гладкими контурами Г,
Теорема Коши (для многосвязной области). Если функция f(z) аналитична в многосвязной области D, ограниченной замкнутыми кусочно-гладкими контурами Г,  ,
,  , ... ,
, ... ,  , и непрерывна в
, и непрерывна в
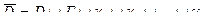 , то
, то
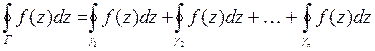
(все контуры пробегаются в положительном направлении).
Интегральная формула Коши . Если функция 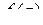 аналитична в односвязной области D, ограниченной замкнутым кусочно-гладким контуром Г, и непрерывна в
аналитична в односвязной области D, ограниченной замкнутым кусочно-гладким контуром Г, и непрерывна в  , то для любой внутренней точки
, то для любой внутренней точки  области D имеет место формула Коши:
области D имеет место формула Коши:
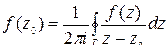 ,
,
а также справедливо обобщающее эту формулу следствие:
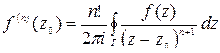 ,
,
где 
Задача 3.1. Вычислить интеграл от функции комплексного переменного по данной кривой.
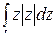 ,
, 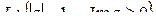 .
.
Решение
Кривая L представляет собой полуокружность, с центром в начале координат, радиусом 1, расположенная в верхней полуплоскости.
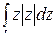 =
= 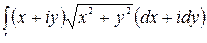 =
= 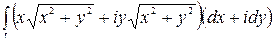 =
=
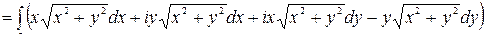 =
=
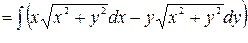 +
+ 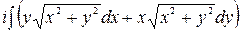 =
=
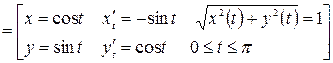 =
= 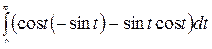 +
+
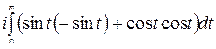 =
= 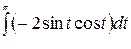 +
+ 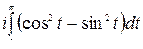 =
=
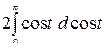 +
+ 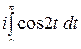 =
= 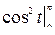 +
+ 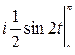 =
= 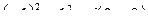 =0
=0
Задача 3.2. Вычислить интеграл: 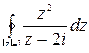 .
.
Решение
Подынтегральная функция 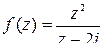 аналитична внутри контура
аналитична внутри контура 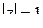 и на нём (единственная точка
и на нём (единственная точка 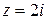 в которой функция не определена находится вне контура интегрирования). По теореме Коши данный интеграл равен нулю.
в которой функция не определена находится вне контура интегрирования). По теореме Коши данный интеграл равен нулю.
Задача 3.3. Вычислить интеграл: 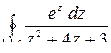 .
.
Решение
Подынтегральная функция теряет аналитичность в точках 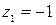 ,
, 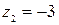 (знаменатель обращается в нуль). Внутри контура находится одна из этих точек
(знаменатель обращается в нуль). Внутри контура находится одна из этих точек  . Перепишем интеграл в виде
. Перепишем интеграл в виде
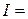
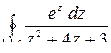 =
= 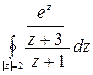 .
.
Функция 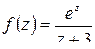 аналитична в круге
аналитична в круге 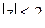 .
.
Применяем интегральную формулу Коши при 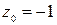
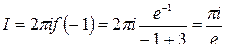
Задача 3.4. Вычислить интеграл 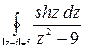 .
.
Решение
 Подынтегральная функция теряет аналитичность в точках
Подынтегральная функция теряет аналитичность в точках 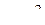 ,
,  расположенных внутри контура
расположенных внутри контура 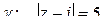 . Непосредственно формулу Коши применять нельзя. Поэтому сначала построим окружности
. Непосредственно формулу Коши применять нельзя. Поэтому сначала построим окружности  и
и  с центрами в точках
с центрами в точках  и
и  соответственно, их радиусы выберем достаточно малыми, чтобы окружности не пересекались и лежали внутри
соответственно, их радиусы выберем достаточно малыми, чтобы окружности не пересекались и лежали внутри  . В трехсвязной области, ограниченной контурами
. В трехсвязной области, ограниченной контурами  ,
,  и
и  , и на ее границе подынтегральная функция аналитична, поэтому по теореме Коши для многосвязной области получаем:
, и на ее границе подынтегральная функция аналитична, поэтому по теореме Коши для многосвязной области получаем:

Далее применяем интегральную формулу Коши
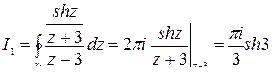 ,
, 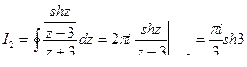
Окончательно получаем 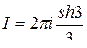 .
.
Дата: 2018-12-21, просмотров: 381.