Идеи, развитые в пункте 1.5.2 в связи с преобразованием плоских областей, естественно, переносятся и на случай пространственных областей.

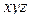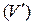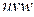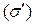Предположим, что даны два трехмерных пространства с системами координат xyz, и uvw. Рассмотрим в этих пространствах две замкнутые области: область (V) в пространстве и область  в пространстве , ограниченные соответственно поверхностями  и , которые мы всегда будем предполагать кусочно-гладкими. Допустим, что эти области связаны между собой взаимно однозначным непрерывным соответствием, которое осуществляется формулами:

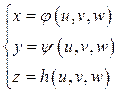                                ,                                               (2.3)

При этом необходимо, чтобы точкам поверхности 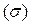 отвечали именно точки поверхности  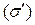и наоборот.

Пусть функции (2.3) имеют в области 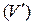 непрерывные частные производные.

Определение 4. Определитель третьего порядка следующего вида   

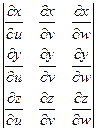                                                                                         (2.4)

называют якобианом перехода от декартовых координат к криволинейным и обозначают .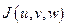

Числа 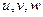, однозначно характеризующие положение точки в пространстве xyz, называются криволинейными координатами этой точки. Точки пространства xyz, для которых одна из этих координат сохраняет постоянное значение, образуют координатную поверхность. Всегда будет существовать три семейства таких координатных поверхностей; через каждую точку области (V) проходит по одной поверхности каждого семейства.

        Тогда формула перехода от декартовых координат к криволинейным координатам будет иметь следующий вид: 

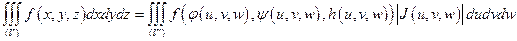       . (2.5)

Замечание 1. На практике рассматривают не два координатных пространствах, а одно совмещенное.

а) Цилиндрические координаты представляют соединение полярных координат в плоскости 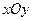 с обычной декартовой аппликатой z (рис. 1.43).

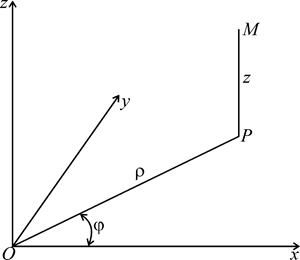
Рисунок 1.43

Формулы, связывающие их с декартовыми координатами, имеют вид:

.

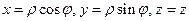Эти формулы отображают область 0 ≤ ρ < +¥, 0 ≤ φ < 2π, –¥ < z < +¥ на все пространство xyz. Отметим, однако, что прямая 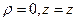 отображается в одну точку (0,0,z); этим нарушается взаимная однозначность соответствия. Координатные поверхности в рассматриваемом случае будут:

а) 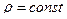 – цилиндрические поверхности с образующими, параллель-ными оси 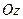; направляющими для них служат окружности на плоскости  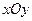с центром в начале;   

б) 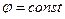 – плоскости, проходящие через ось ;

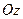в) 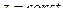 – плоскости, параллельные плоскости .

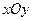      По формуле (2.4) получаем якобиан преобразования:

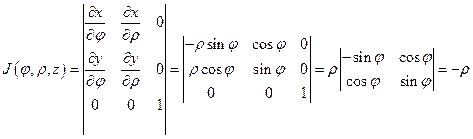     ,        (2.6)

а формула перехода (2.5) принимает вид

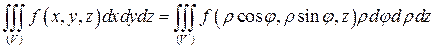.                (2.7)

б) Сферические координаты связаны с декартовыми формулами:

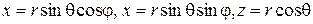            ,                         (2.8)

где .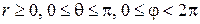

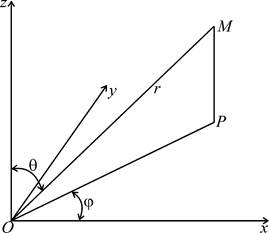
Рисунок 1.44

Геометрический смысл величин 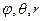 ясен из рисунка 1.44: r есть радиус-вектор OM, соединяющий начало с данной точкой M;  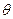– угол, составляемый этим радиус-вектором с осью Oz;  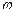– угол, составляемый с осью Ox проекцией  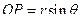радиус-вектора OM на плоскость xOy.

Координатные поверхности составляют три семейства:

а) 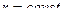- концентрические сферы с центром в начале координат;

б) 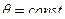 - круговые конусы, осью

которых служит ось Oz;

в) 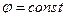 - плоскости, проходящие через ось Oz.

     По формуле (2.4) получаем якобиан преобразования:

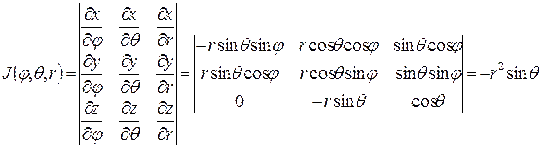   , (2.9)

а формула перехода (2.5) принимает вид

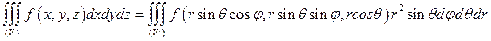.   (2.10)