Комплексные числа и действия над ними
Комплексным числом z называется выражение  , где
, где 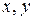 –действительные числа,
–действительные числа, 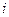 – мнимая единица
– мнимая единица 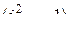 . При этом число
. При этом число 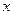 называется действительной частью, а
называется действительной частью, а  – мнимой частью числа z и обозначаются:
– мнимой частью числа z и обозначаются:  .
.
Комплексное число  называется сопряженным числу
называется сопряженным числу  .
.
Действия над комплексными числами 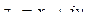 и
и 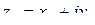 определяются следующими формулами:
определяются следующими формулами:
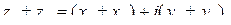
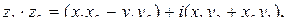
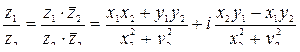
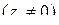 .
.

Комплексное число  изображается на плоскости точкой M с координатами
изображается на плоскости точкой M с координатами 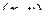 или вектором
или вектором 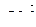 . Длина
. Длина 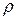 этого вектора называется модулем комплексного числа z, обозначается
этого вектора называется модулем комплексного числа z, обозначается 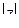 и вычисляется
и вычисляется 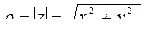 . Угол
. Угол 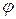 между положительным направле-нием оси
между положительным направле-нием оси  и вектором
и вектором 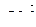 называется аргументом комплексного числа z и обозначается
называется аргументом комплексного числа z и обозначается 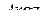 ; он определен с точностью до слагаемого, кратного
; он определен с точностью до слагаемого, кратного 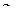 . Значение аргумента
. Значение аргумента  , удовлетворяющего условию
, удовлетворяющего условию 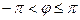 (или
(или 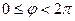 ), называется главным и обозначается
), называется главным и обозначается 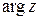 . Таким образом,
. Таким образом,
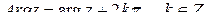
Комплексное число 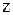 можно записать с помощью модуля и аргумента:
можно записать с помощью модуля и аргумента:
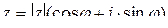 – тригонометрическая форма,
– тригонометрическая форма,
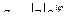 – показательная форма.
– показательная форма.
Запись 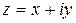 называется алгебраической формой комплексного числа z.
называется алгебраической формой комплексного числа z.
Задача 1.1. Заданы комплексные числа: а) 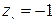 , б)
, б) 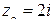 , в)
, в) 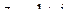 , г)
, г) 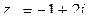 , д)
, д) 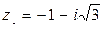 , е)
, е) 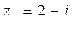 . Представить
. Представить 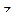 ,
, 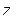 ,
,  в тригонометрической форме, а
в тригонометрической форме, а 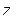 ,
,  ,
,  – в показательной форме и изобразить точками на комплексной плоскости.
– в показательной форме и изобразить точками на комплексной плоскости.
Решение
 а) для
а) для 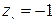 имеем
имеем 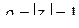 ,
, 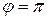 , тогда
, тогда 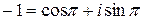 ;
;
б) для 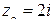 имеем
имеем 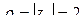 ,
, 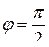 , тогда
, тогда 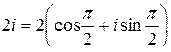 ;
;
в) для 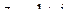 имеем
имеем
 ,
, 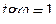 ,
, 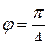 , тогда
, тогда 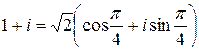
г) для 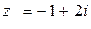 имеем
имеем
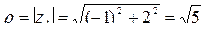 ,
,  ,
, 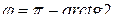 , тогда
, тогда 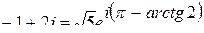
д) для 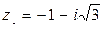 имеем
имеем 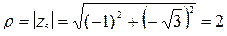 ,
, 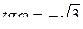 ,
, 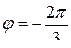 или
или 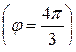 , тогда
, тогда 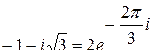
e) для 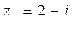 имеем
имеем 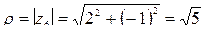 ,
, 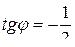 ,
,
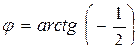 , тогда
, тогда 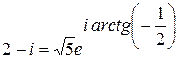
Над комплексными числами z, z1, z2, заданными в тригонометрической форме:
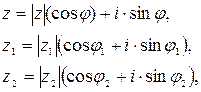
действия можно выполнять по правилам:

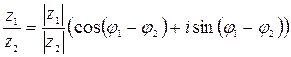
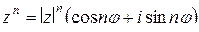 ,
, 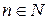 - формула Муавра.
- формула Муавра.
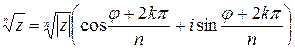 ,
, 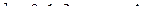 .
.
Здесь под 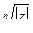 понимается арифметический корень.
понимается арифметический корень.
Из последней формулы видно, что 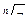 при
при 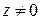 имеет ровно n различных значений.
имеет ровно n различных значений.
Задача 1.2. Найти все значения корня: а) 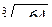 , б)
, б) 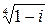 .
.
Решение
а) для  ,
, 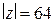 ,
, 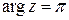 , так что в тригонометрической форме это число имеет вид
, так что в тригонометрической форме это число имеет вид  . Согласно формуле для
. Согласно формуле для 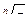 имеем:
имеем:
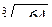 =
= 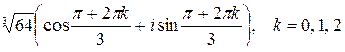 то есть:
то есть:
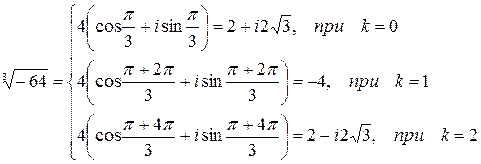
Ответ: 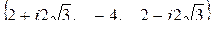
б) для 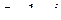 ,
, 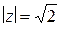 ,
, 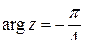 . В тригонометрической форме
. В тригонометрической форме
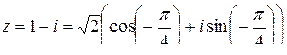
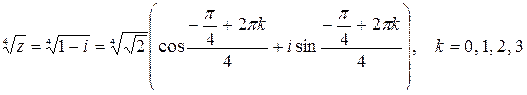
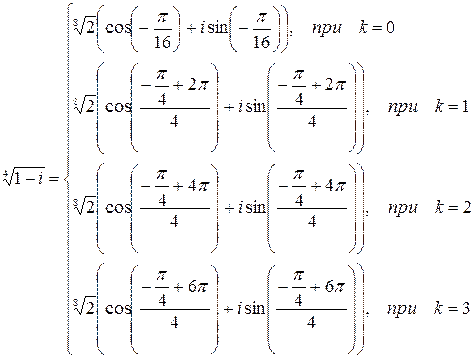
Ответ:
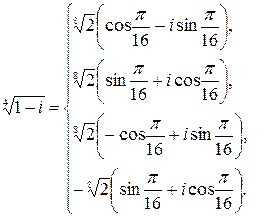
Задача 1.3. Вычислить степень и представить результат в алгебраи-ческой форме:
а) 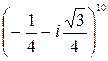 ; б)
; б) 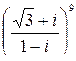 .
.
Решение
а) запишем 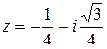 в тригонометрической форме:
в тригонометрической форме:
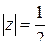 ,
, 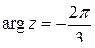 .
.
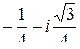 =
= 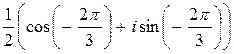 .
.
По формуле Муавра:
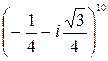 =
= 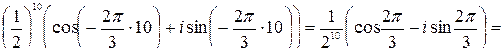
= 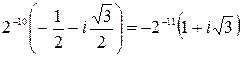
б) пусть 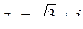 и
и  .
.
Тогда  ,
,  ,
, 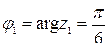 ,
, 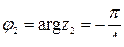 .
.
По правилу деления 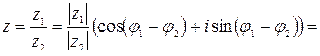
= 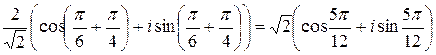 .
.
По формуле Муавра:
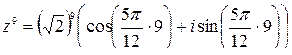 =
= 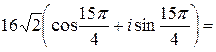

= 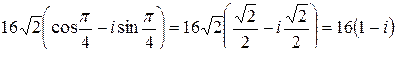 .
.
Задача 1.4. Найти множества точек z на плоскости, удовлетворяю-щих следующим условиям:
a) 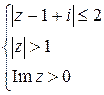 ; б)
; б) 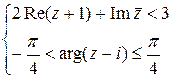 .
.
При решении задач такого типа можно от комплексной переменной z перейти к двум действительным переменным x и y. Тогда исходные условия для z сведутся к соответствующим условиям для действительных переменных x и y . Так, неравенство Im z>0, учитывая z = x+iy, преобразуется к неравенству y>0.
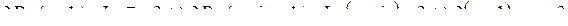 .
.
Однако в ряде случаев нецелесообразно переходить к x и y, а лучше использовать геометрический смысл уравнений или неравенств с комплексной переменной.
Так, уравнение 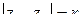 задает окружность с центром в точке z0 и радиусом r, а неравенства
задает окружность с центром в точке z0 и радиусом r, а неравенства 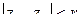 и
и 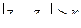 соответственно внутрен-нюю и внешнюю открытые области круга ограниченные данной окружностью.
соответственно внутрен-нюю и внешнюю открытые области круга ограниченные данной окружностью.
Неравенство 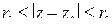 задаёт кольцо ограниченное окружностями радиусов
задаёт кольцо ограниченное окружностями радиусов 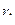 и
и  с центром в точке
с центром в точке  , причем границы кольца, окружности
, причем границы кольца, окружности 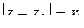 и
и 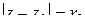 , принадлежат этой кольцевой области.
, принадлежат этой кольцевой области.
Уравнение 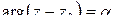 задаёт луч, исходящий из точки
задаёт луч, исходящий из точки  под углом
под углом 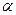 к оси Ox.
к оси Ox.
Решение
 a) в соответствии с вышеизложен-ным, неравенство
a) в соответствии с вышеизложен-ным, неравенство 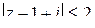 опреде-ляет круг с центром
опреде-ляет круг с центром  и радиусом 2. Неравенство
и радиусом 2. Неравенство 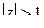 внешность круга с центром
внешность круга с центром 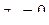 радиуса 1. Неравенство
радиуса 1. Неравенство  определяет верхнюю полуплоскость плоскости
определяет верхнюю полуплоскость плоскости 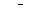
Изображаем все три указанные области и находим их пересечение. Это и будет искомое множество. Пунктир означает, что граница не принадлежит множеству.
б) 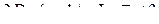
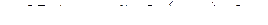
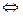
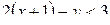
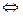
 .
.
 Уравнение y =2x-1 определяет прямую, разбивающую плоскость на две полу-плоскости. Очевидно, та из них, которая содержит начало координат, задаётся неравенством
Уравнение y =2x-1 определяет прямую, разбивающую плоскость на две полу-плоскости. Очевидно, та из них, которая содержит начало координат, задаётся неравенством  . Уравнение
. Уравнение 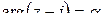 определяет луч с началом в точке
определяет луч с началом в точке 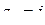 , наклоненный к оси Ox под углом
, наклоненный к оси Ox под углом 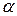 . Неравенство
. Неравенство 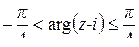 задаёт все те лучи с началом в точке
задаёт все те лучи с началом в точке 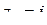 , для которых
, для которых 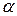 удовлетворяет неравенству
удовлетворяет неравенству 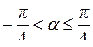 , то есть задаёт угловой сектор с вершиной
, то есть задаёт угловой сектор с вершиной 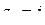 и сторонами, образующими с Ox углы
и сторонами, образующими с Ox углы 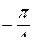 и
и 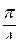 (при этом первая сторона не принадлежит сектору, а вторая принадлежит). Пересечение соответствующих областей образует искомое множество.
(при этом первая сторона не принадлежит сектору, а вторая принадлежит). Пересечение соответствующих областей образует искомое множество.
Дата: 2018-12-21, просмотров: 424.