Говорят, что в области D (пространственной или плоской) задано скалярное поле, если каждой точке M из D поставлено в соответствие некоторое число. Тем самым в области D определена скалярная функция u ( M ). Если ввести некоторую систему координат, например, трехмерную декартову, то точка М будет определяться тройкой чисел х, у, z, а задание поля u ( M ) сведется к заданию функции от трех переменных, которую будем обозначать той же буквой u: u ( x , y , z ).
Термином «поле» подчеркивается тот факт, что значение функции u зависит только от точек М и не зависит от того, в каких координатах задаются эти точки.
Пусть u ( M ) – некоторое скалярное поле в области D и М0 – внутренняя точка из D. Возьмем вектор (луч) 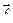 с началом в точке М0 и произвольную точку
с началом в точке М0 и произвольную точку 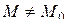 на
на 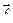 (так, чтобы отрезок
(так, чтобы отрезок 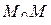 целиком принадлежал области D).
целиком принадлежал области D).
Определение. Производной скалярного поля u в точке 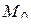 по направлению
по направлению 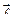 называется предел отношения разности
называется предел отношения разности 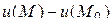 к длине отрезка
к длине отрезка 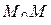 , когда
, когда 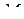 стремится к
стремится к 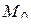 по лучу
по лучу 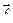 :
:
 .
.
Пусть поле u задано в декартовой системе координат, т.е. 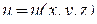 .
.
Теорема 1. Если функция 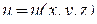 дифференцируема в точке
дифференцируема в точке 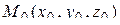 , то в этой точке существует производная поля u по любому направлению, причем
, то в этой точке существует производная поля u по любому направлению, причем
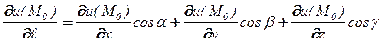 , (1)
, (1)
где 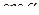 ,
, 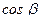 ,
, 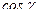 – направляющие косинусы вектора
– направляющие косинусы вектора 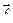 .
.
Пример 1 . Найти производную скалярного поля 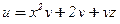 в точке
в точке 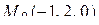 в направлении вектора
в направлении вектора 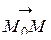 ,
, 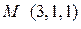 .
.
Решение
Находим частные производные функции 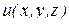 и вычисляем их значения в точке
и вычисляем их значения в точке  :
:
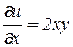 ,
, 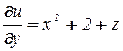 ,
, 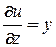 ;
;
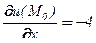 ,
, 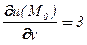 ,
, 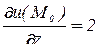 .
.
Вектор 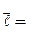
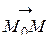 имеет вид:
имеет вид: 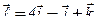 , а единичный вектор того же направления представим в виде:
, а единичный вектор того же направления представим в виде:
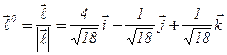 .
.
Следовательно,
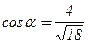 ,
, 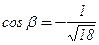 ,
,  .
.
По формуле (1) получим:
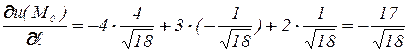 .
.
Определение. Градиентом скалярного поля 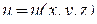 в точке
в точке 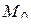 называется вектор
называется вектор 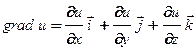 , где частные производные вычисляются в точке
, где частные производные вычисляются в точке 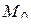 (предполагается, что они существуют).
(предполагается, что они существуют).
Это определение использует декартову систему координат. Можно дать другое, инвариантное определение градиента. Действительно, из формулы (1) следует, что 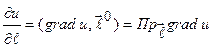 , где
, где 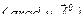 – скалярное произве-дение.
– скалярное произве-дение.
Таким образом, градиент скалярного поля u в точке 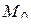 – это вектор, проекция которого на любое направление
– это вектор, проекция которого на любое направление 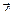 равна производной поля
равна производной поля 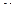 в точке
в точке 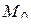 в направлении
в направлении 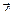 .
.
Отсюда, в частности, можно сделать следующий вывод: если поверхность S задана уравнением  , то единичная нормаль к этой поверхности в точке
, то единичная нормаль к этой поверхности в точке 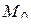 может быть найдена через градиент скалярного поля v по формуле
может быть найдена через градиент скалярного поля v по формуле
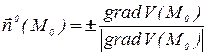 . (2)
. (2)
Знак «+» берется в случае, когда направление искомой нормали и градиента совпадают, а «-» – в противном случае.
Пример 2 . Найти производную скалярного поля 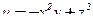 в точке
в точке 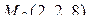 в направлении нормали к поверхности
в направлении нормали к поверхности 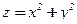 , образующей острый угол с положительным направлением оси OZ.
, образующей острый угол с положительным направлением оси OZ.
Решение
Воспользуемся формулой 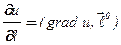 , где
, где 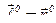 – указанная единичная нормаль к поверхности S в точке
– указанная единичная нормаль к поверхности S в точке 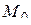 .
.
Найдем градиент поля u в т. 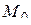 (в координатной форме):
(в координатной форме):
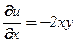 ,
, 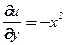 ,
, 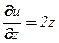 ;
;
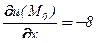 ,
, 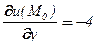 ,
,  ;
;
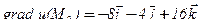 .
.
Для нахождения нормали 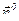 воспользуемся формулой (2). В нашем случае поверхность S задана уравнением
воспользуемся формулой (2). В нашем случае поверхность S задана уравнением 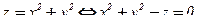 . Поэтому возьмем
. Поэтому возьмем 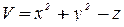 .
.
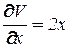 ,
, 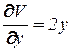 ,
, 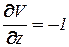 ;
;
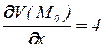 ,
, 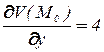 ,
, 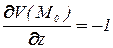 ;
;
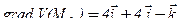 ,
,
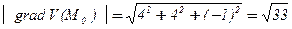 .
.
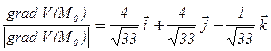 – это одна из двух противоположных по направлению единичных нормалей к S.
– это одна из двух противоположных по направлению единичных нормалей к S.
По условию нормаль образует с осью OZ острый угол и, значит, ее проекция на ось OZ положительна; у последнего вектора она отрицательна. Следовательно, в формуле (2) нужно взять знак минус:
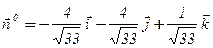 .
.
Окончательно находим:
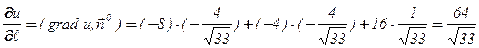 .
.
Пример 3 . Найти угол между градиентами скалярных полей
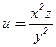 и
и 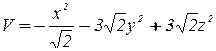 в точке
в точке 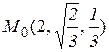 .
.
Решение
Известно, что угол 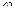 между двумя ненулевыми векторами
между двумя ненулевыми векторами 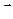 и
и 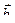 находится из формулы
находится из формулы
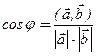 .
.
Воспользуемся этой формулой для 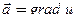 и
и 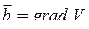 .
.
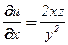 ,
, 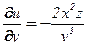 ,
, 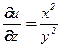 ;
;
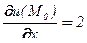 ,
, 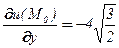 ,
, 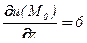 ;
;
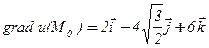 ,
,
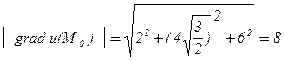 .
.
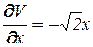 ,
, 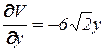 ,
,  ;
;
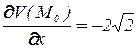 ,
, 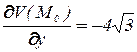 ,
, 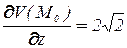 ;
;
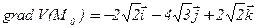 ,
,
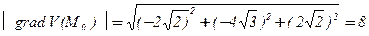 .
.
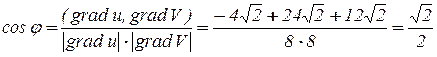 .
.
Следовательно, 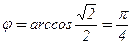 .
.
Дата: 2018-12-21, просмотров: 403.