Говорят, что в области D (пространственной или плоской) задано векторное поле, если каждой точке М из D поставлен в соответствие некоторый вектор 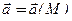 . Если введена прямоугольная декартова система координат, то векторное поле определит в D некоторую векторную функцию от координат точки М:
. Если введена прямоугольная декартова система координат, то векторное поле определит в D некоторую векторную функцию от координат точки М: 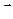
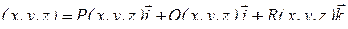 - для пространственной области или
- для пространственной области или 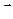
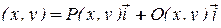 - для плоской области. В дальнейшем будем предполагать, что скалярные функции
- для плоской области. В дальнейшем будем предполагать, что скалярные функции 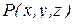 ,
, 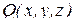 ,
, 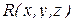 имеют непрерывные частные производные в D, т.е. поле
имеют непрерывные частные производные в D, т.е. поле 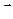
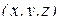 непрерывно дифференцируемое. Для геометрической характеристики векторного поля вводят понятие векторной линии.
непрерывно дифференцируемое. Для геометрической характеристики векторного поля вводят понятие векторной линии.
Определение. Векторной линией поля 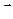 называется гладкая кривая, в каждой точке М которой касательная имеет то же направление, что и вектор
называется гладкая кривая, в каждой точке М которой касательная имеет то же направление, что и вектор 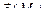 .
.
Векторные линии поля 
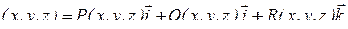 определяются системой дифференциальных уравнений
определяются системой дифференциальных уравнений
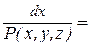

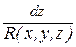 . (3)
. (3)
Аналогично, если поле имеет вид 
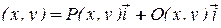 , то уравнение векторных линий имеет вид:
, то уравнение векторных линий имеет вид:
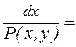
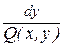 . (4)
. (4)
Пример 4 . Найти векторные линии поля 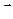
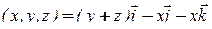 .
.
Решение.
В данном случае 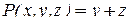 ,
,  и система (3) принимает вид:
и система (3) принимает вид:
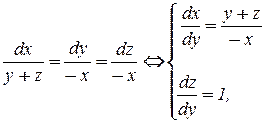 ,
,
где 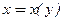 ,
, 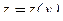 – неизвестные функции. Из второго уравнения получаем:
– неизвестные функции. Из второго уравнения получаем: 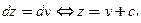 . Подставим в первое уравнение:
. Подставим в первое уравнение: 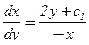 . Это уравнение с разделяющимися переменными.
. Это уравнение с разделяющимися переменными.
Решаем его:
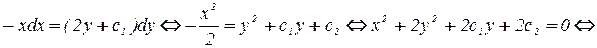
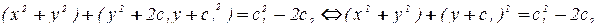 .
.
Но 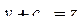 , следовательно,
, следовательно, 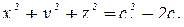 .
.
Обозначив 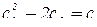 , получим x2+y2+z2= c.
, получим x2+y2+z2= c.
Итак, векторные линии поля 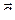 определяются системой алгебраических уравнений
определяются системой алгебраических уравнений  . Это семейство пространственных кривых, которые получаются пересечением сфер x2+y2+z2= c и плоскостей z = y+c1, параллельных оси ОХ.
. Это семейство пространственных кривых, которые получаются пересечением сфер x2+y2+z2= c и плоскостей z = y+c1, параллельных оси ОХ.
Пример 5 . Найти векторные линии поля 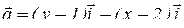 .
.
Решение
Воспользуемся уравнением (4), которое в данном случае принимает вид: 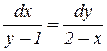 .
.
Решая это уравнение с разделяющимися переменными, получим:
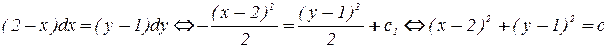 .
.
Таким образом, векторные линии представляют собой окружности в плоскости ХОУ с центром в точке (2; 1).
Поток векторного поля
Определение. Потоком векторного поля 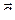 через поверхность S в направлении нормали
через поверхность S в направлении нормали 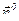 к поверхности S называется поверхностный интеграл первого рода
к поверхности S называется поверхностный интеграл первого рода
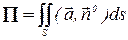 , (5)
, (5)
где 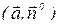 – скалярное произведение.
– скалярное произведение.
Пример 6 . Найти поток векторного поля
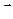
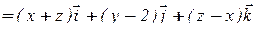
через поверхность S:  ,
, 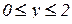 (нормаль внешняя).
(нормаль внешняя).
Решение
Поверхность S представляет собой круговой конус, ось которого совпадает с осью ОУ (рис. 2.1).
Найдем единичную нормаль к поверхности S по формуле (2), для чего рассмотрим скалярное поле 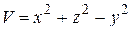 :
:
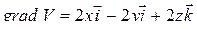 ,
,
 .
.
Так как интеграл (5) берется по поверхности S, а на ней 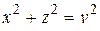 , то
, то 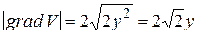 .
.
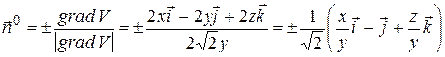 .
.

Рисунок 2.1
Нормаль к внешней стороне конуса S образует с осью ОУ тупой угол, т.е. ее проекция на ось ОУ отрицательна. Следовательно, в последней формуле нужно взять знак «+»:
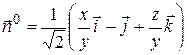 .
.
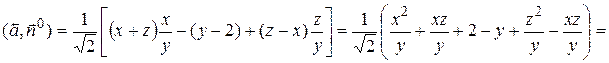
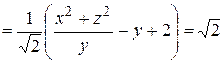 (на S
(на S 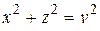 ).
).
Итак, 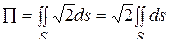 . Последний интеграл равен площади S б боковой поверхности конуса S. Так как
. Последний интеграл равен площади S б боковой поверхности конуса S. Так как 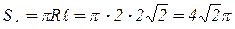 , то
, то 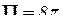 .
.
В последнем примере вычисление поверхностного интеграла свелось к вычислению площади поверхности S. В более общем случае приходится использовать ту или иную формулу вычисления поверхностных интегралов.
Пусть, например, поверхность S однозначно проектируется на плоскость ХОУ. Тогда ее можно задать уравнением 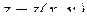 , а поверхностный интеграл (5) можно свести к двойному интегралу по формуле:
, а поверхностный интеграл (5) можно свести к двойному интегралу по формуле:
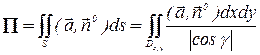 , (6)
, (6)
где 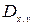 – проекция поверхности S на плоскость ХОУ, а
– проекция поверхности S на плоскость ХОУ, а 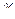 – угол единичной нормали к
– угол единичной нормали к  с осью О Z. Заметим, что
с осью О Z. Заметим, что 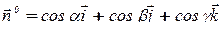 , поэтому
, поэтому  получаем при нахождении нормали
получаем при нахождении нормали 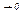 .
.
Если поверхность 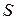 не проектируется однозначно ни на одну из координатных плоскостей, то ее разбивают на части, каждая из которых однозначно проектируется на ту или иную координатную плоскость.
не проектируется однозначно ни на одну из координатных плоскостей, то ее разбивают на части, каждая из которых однозначно проектируется на ту или иную координатную плоскость.
Пример 7 . Найти поток поля 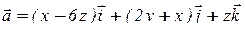 через часть плоскости
через часть плоскости 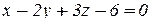 , вырезаемую координатными плоскостями (нормаль образует острый угол с осью OZ).
, вырезаемую координатными плоскостями (нормаль образует острый угол с осью OZ).
Решение
Нормаль к поверхности 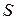 можно найти по формуле (2), но проще учесть, что в уравнении плоскости коэффициенты при x , y , z являются координатами некоторого перпендикулярного к плоскости вектора, т.е. вектор
можно найти по формуле (2), но проще учесть, что в уравнении плоскости коэффициенты при x , y , z являются координатами некоторого перпендикулярного к плоскости вектора, т.е. вектор 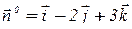 является нормалью к
является нормалью к 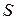 .
.
Тогда 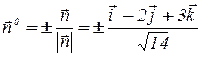 .
.
Отсюда, в частности, получаем: 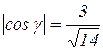 , а так как по условию нормаль образует острый угол с осью OZ, то нужно взять знак «+», т.е.
, а так как по условию нормаль образует острый угол с осью OZ, то нужно взять знак «+», т.е.
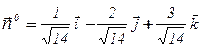 ;
;
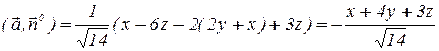 .
.

| ||
| Рисунок 2.2 |
В данном примере поверхность 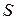 (треуголь-ник) однозначно проекти-руется на каждую из координатных плоскостей. Возьмем для определенно-сти проекцию на плоскость ХОУ (см. рис. 2.2).
(треуголь-ник) однозначно проекти-руется на каждую из координатных плоскостей. Возьмем для определенно-сти проекцию на плоскость ХОУ (см. рис. 2.2).
Уравнение плоскости запишем в виде
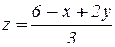
и подставим правую часть вместо z в 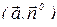 :
:
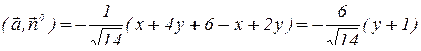 .
.
По формуле (6) получим:
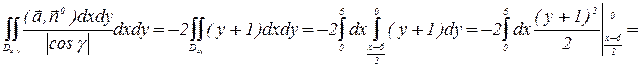
 .
.
Пример 8 . Найти поток поля 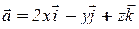 через замкнутую поверхность
через замкнутую поверхность 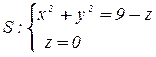 (нормаль внешняя).
(нормаль внешняя).
Решение
|
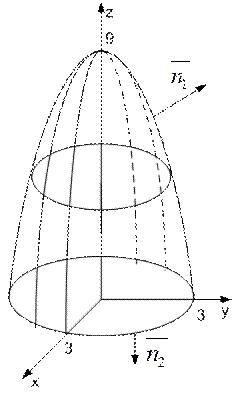
| Рисунок 2.3 |
Поверхность 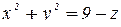
представляет собой параболоид вращения (рис. 2.3), т.е. поверхность S состоит из части S1 параболоида и части S2 плоскости z =0.
Поток через поверхность S будет равен сумме потоков 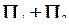 через S1 и S2 соответственно. Для нахождения нормали
через S1 и S2 соответственно. Для нахождения нормали 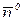 к S1 рассмотрим скалярное поле
к S1 рассмотрим скалярное поле 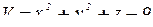 и воспользуемся формулой (2).
и воспользуемся формулой (2).
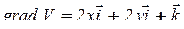 ,
,
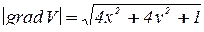 ;
;
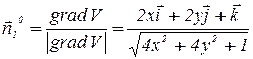
(при выборе знака нормали учли, что ее проекция на ось OZ положительна для внешней стороны S1).
Заметим, что поверхность S1 однозначно проектируется на плоскость ХОУ, поэтому воспользуемся формулой (6):
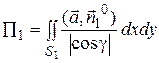 .
.
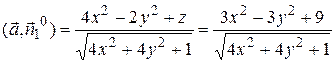 ,
, 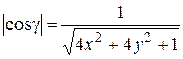 .
.
Следовательно,
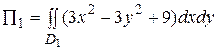 ,
,
где D 1 – проекция 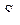 на плоскость ХОУ – круг
на плоскость ХОУ – круг 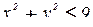 . Очевидно, последний интеграл удобнее вычислить в полярных координатах:
. Очевидно, последний интеграл удобнее вычислить в полярных координатах:
 ,
, 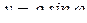 .
.
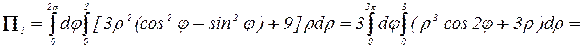
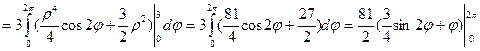
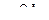 .
.
На поверхности S2 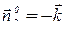 и
и  , поэтому
, поэтому 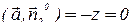 и
и 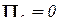 .
.
Таким образом, суммарный поток равен 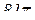 .
.
Дата: 2018-12-21, просмотров: 382.