Определение. Линейным интегралом векторного поля
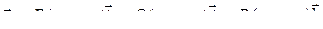
вдоль кривой АВ называется криволинейный интеграл второго рода:
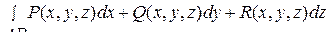. (8)
Если ввести обозначение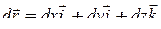 
( 
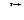– дифференциал радиус-вектора точек кривой АВ), то интеграл (8) можно записать в ви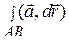де 
, где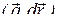 
– скалярное произведение. Если кривая АВ задана параметрически: 
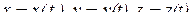или
в векторной форме: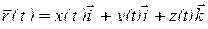 
,
где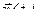 
– параметрическое задание радиус-вектора точек кривой АВ, то линейный интеграл примет вид:
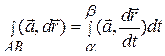, (9)
где 
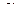и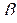 
– значения параметра, соответствующие начальной и конечной точкам кривой АВ.
В случае, когда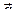 
– силовое поле, линейный интеграл выражает работу, совершаемую полем 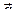при перемещении материальной точки по кривой АВ.
Пример 11 . Найти работу W силы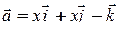 
вдоль одного витка АВ винтовой линии: 
( 
).
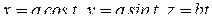Решение
Кривая АВ задана параметрически:
.
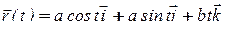Воспользуемся формулой (9).
;
;
, 
, 
;
.
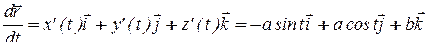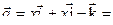
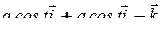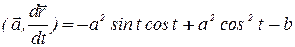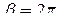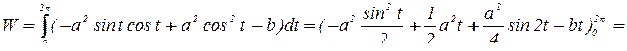
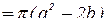Определение. Циркуляцией поля 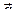по замкнутой ориентированной кривой (контуру) 
называется линейный интеграл поля 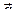вдоль .
Пример 12 . Вычислить циркуляцию поля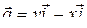 
вдоль контура : 
, 
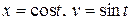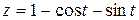в направлении возрастания параметра.
Решение
Контур задан параметрически, но не указаны пределы изменения параметра t. Найдем их. Если точка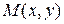 
пробегает контур , то точка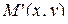 
– проекция точки 
на плоскость ХОУ – пробегает единичную окружность: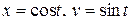 
. Таким образом, можно считать, что параметр t меняется от 0 до 2π (циркуляция ищется в направлении возрастания параметра!). Заметим, что пр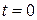и 
и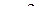 
соответствующие точки на контуре совпадают, т.е. контур обходится полностью ( есть линия пересечения кругового цилиндра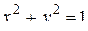 
с плоскостью 
).
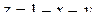Воспользуемся формулой (9):
= 
,
,
;
;
.
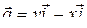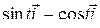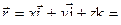
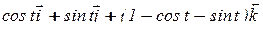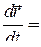
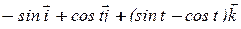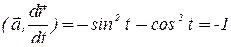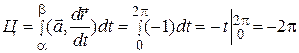Пример 13 . Найти модуль циркуляции поля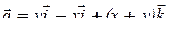 
вдоль контура 
.
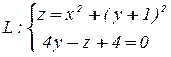Решение
В данном примере контур задан как линия пересечения параболоида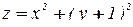 
и плоскости 
.
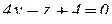Зададим контур параметрически (такое задание неоднозначно, но выберем одно из простейших).
Найдем проекцию контура на плоскость ХОУ, для чего исключим переменную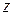 
из системы, задающей :
.
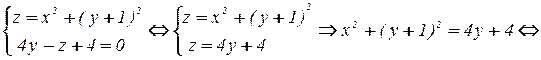
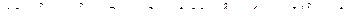Очевидно, что проекция представляет собой окружность радиуса 2 с центром в точке (0;1), поэтому естественно взять
, 
, .
Тогда
,
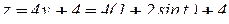т.е. , 
, 
.
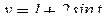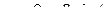Применим формулу (9):
,
,
,
;
.
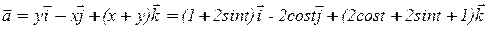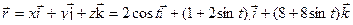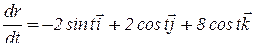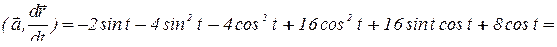
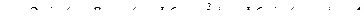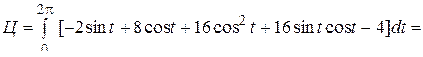
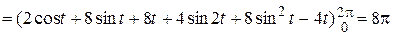Ротор. Формула Стокса
Определение. Ротором (вихрем) векторного поля
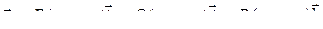
называется векторное поле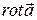 
, определяемое равенством
.
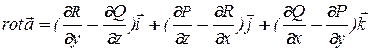Для нахождения ротора поля 
удобно использовать формальный определитель:
,
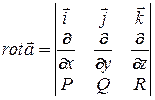причем под произведениями вида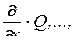 
понимаются частные производ-ные 
.
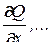Например, 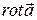, где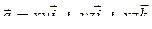 
, равен:
.
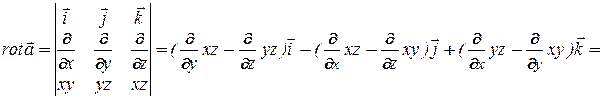
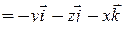Теорема 3 . Пусть функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывно дифференцируемы в некоторой пространственной области и S – некоторая кусочно-гладкая поверхность в этой области, ограниченная кусочно-гладким контуром L. Тогда имеет место равенство:
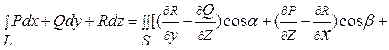
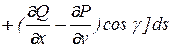, (10)
где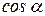 
, 
, 
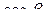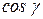– направляющие косинусы нормали 
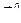к поверхности 
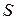, причем направление нормали выбирается так, чтобы из ее конца обход контура наблюдался против часовой стрелки.
Если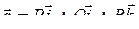 
, а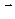 
– радиус-вектор точек контура L, то формулу (10) можно записать в векторной форме:
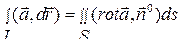. (10.1)
Формулу (10) – (10.1) называют формулой Стокса .
Формулу Стокса можно использовать для вычисления циркуляции:
.
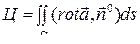Пример 13 . (См. условие выше). Найдем циркуляцию с использова-нием формулы (10.1). В качестве поверхности , ограниченной контуром , возьмем часть плоскости 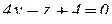. Нормаль 
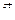к этой поверхности имеет проекции (0, 4, -1), а единичная нормаль 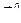имеет вид
.
,
.
, 
, 
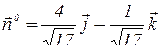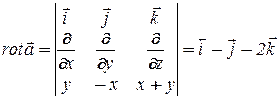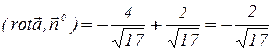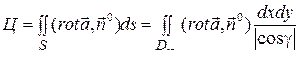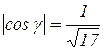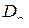– проекция 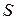на плоскость ХОУ – круг радиуса 2.
Следовательно,
; 
.
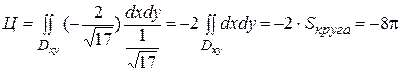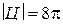Пример 14 . Найти модуль циркуляции вектора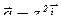 
по границе части сферы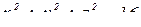 
, расположенной в 1-ом октанте.
Решение
В качестве поверхности 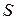, ограниченной контуром , возьмем соответствующую часть сферы (часть плоскости брать нельзя, так как контур не лежит в одной плоскости). Единичную нормаль 
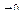к 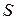найдем по формуле (2), 
:
,
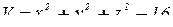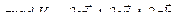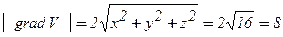на ;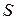
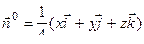(здесь направление нормали не существенно, так как ищется модуль циркуляции).
, 
, 
.
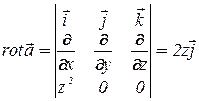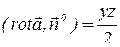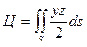Последний интеграл сведем к двойному, спроектировав, например, поверхность 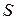на плоскость ХОУ; проекция 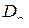- четверть круга 
.
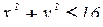Так как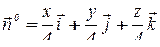 
, то 
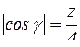
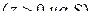и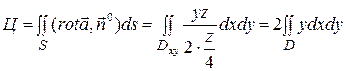 
.
Переходя к полярным координатам, получим
.
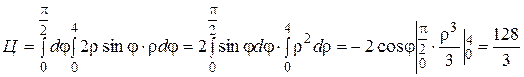Пример 15 . Вычислить модуль циркуляции поля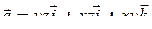 
вдоль контура 
.
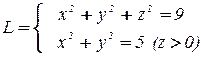Решение
Контур получен пересечением сферы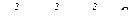 
с цилиндром 
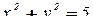и представляет собой окружность, лежащую в плоскости 
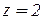. Поэтому в качестве поверхности 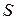естественно взять круг. Тогда нормалью 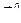к 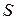будет орта 
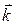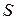
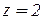. На и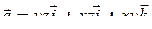 
,
,
.
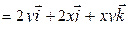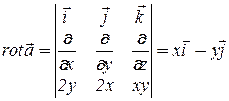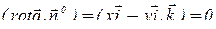Следовательно, циркуляция равна нулю: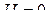 
.
Дата: 2018-12-21, просмотров: 319.
