¨Если 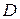 – некоторое множество точек комплексной плоскости и каждому числу
– некоторое множество точек комплексной плоскости и каждому числу  из
из 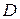 поставлено в соответствие единственное комплексное число
поставлено в соответствие единственное комплексное число  , то говорят, что на множестве
, то говорят, что на множестве 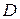 определена однозначная функция комплексного переменного (ФКП), и пишут
определена однозначная функция комплексного переменного (ФКП), и пишут
 ,
,
где  – действительная часть функции
– действительная часть функции 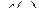 ,
,
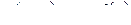 – мнимая её часть.
– мнимая её часть.
¨Если каждому числу  из
из 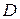 поставлено в соответствие неединственное комплексное число
поставлено в соответствие неединственное комплексное число  , то говорят, что на множестве
, то говорят, что на множестве 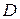 задана многозначная функция комплексного переменного.
задана многозначная функция комплексного переменного.
Основные элементарные ФКП определяются следующими формулами:
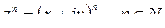

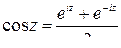 ;
; 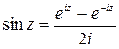 ;
;
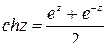 ;
;  ;
;
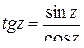 ;
;  ;
; 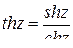 ;
; 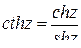 ;
;
 – это многозначная функция, главное значение логарифмической функции берётся при
– это многозначная функция, главное значение логарифмической функции берётся при 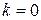 и обозначается
и обозначается  .
.
Задача 2.1. Доказать, что функция 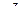 имеет период
имеет период 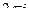 .
.
Решение
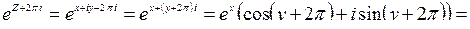
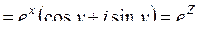
Замечание. ФКП  и
и 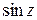 могут принимать значения, которые по модулю превосходят единицу.
могут принимать значения, которые по модулю превосходят единицу.
Задача 2.2. Найти 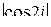 .
.
Решение
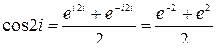 . Поэтому
. Поэтому 
Задача 2.3. Вычислить Ln (-1) и ln (-1).
Решение
Так как  , а
, а  , получаем
, получаем

где 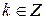 .
. 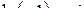
Задача 2.4 . Найти действительную и мнимую части функции 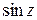 .
.
Решение
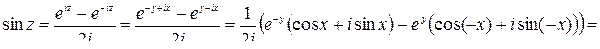
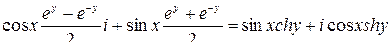 ,
,
отсюда 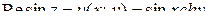 ,
, 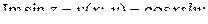
Если 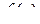 – однозначная ФКП в области
– однозначная ФКП в области  , то производной
, то производной 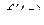 функции
функции 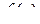 в точке
в точке  называется
называется 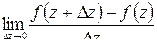 . Функция, имеющая производную в точке
. Функция, имеющая производную в точке 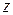 , называется дифференцируемой в этой точке.
, называется дифференцируемой в этой точке.
Теорема (необходимое и достаточное условие дифференци-руемости.) Для того чтобы функция 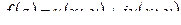 в точке
в точке  была дифференцируема, необходимо и достаточно, чтобы функции
была дифференцируема, необходимо и достаточно, чтобы функции 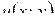 и
и 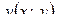 были дифференцируемы в точке
были дифференцируемы в точке 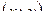 и удовлетворяли в этой точке условиям Коши-Римана:
и удовлетворяли в этой точке условиям Коши-Римана:
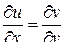 и
и 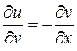 .
.
При выполнении условий Коши-Римана справедлива формула:
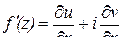 (3.1)
(3.1)
▪ Функция f(z) называется аналитической в точке z, если она дифференцируема в некоторой окрестности этой точки.
▪ Функция f(z) называется аналитической в области 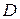 , если она аналитична в каждой точке этой области.
, если она аналитична в каждой точке этой области.
Задача 2.4. Выяснить, в каких точках дифференцируема функция 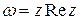 .
.
Решение
Имеем  ,
,  и
и  .
.
Функции 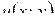 и
и 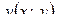 дифференцируемы для любых
дифференцируемы для любых  и
и  .
.
Проверим условия Коши-Римана:
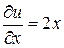 ,
, 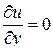 ,
,  ,
,  .
.
Они выполняются только при  и
и  . Поэтому функция
. Поэтому функция 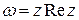 дифференцируема только в точке
дифференцируема только в точке 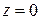 .
.
Замечание. Функция 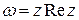 не является аналитической ни в одной точке комплексной плоскости. (Почему?)
не является аналитической ни в одной точке комплексной плоскости. (Почему?)
Задача 2.5. Доказать, что функция 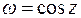 аналитична во всей комплексной плоскости, и найти её производную.
аналитична во всей комплексной плоскости, и найти её производную.
Решение
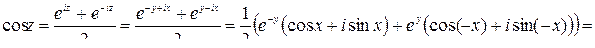
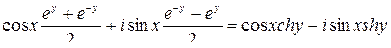 ,
,
отсюда  ,
,  .
.
Находим
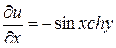 ,
, 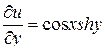 ,
, 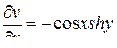 ,
, 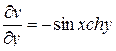 .
.
Замечаем, что функции 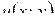 и
и 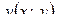 дифференцируемы, и условия Коши-Римана выполняются в любой точке
дифференцируемы, и условия Коши-Римана выполняются в любой точке 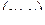 . Поэтому функция
. Поэтому функция  аналитична во всей комплексной плоскости. В соответствии с формулой (3.1) и результатами задачи (2.4) получаем:
аналитична во всей комплексной плоскости. В соответствии с формулой (3.1) и результатами задачи (2.4) получаем:
 .
.
Функция 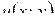 , имеющая непрерывные частные производные второго порядка на области
, имеющая непрерывные частные производные второго порядка на области 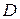 и удовлетворяющая уравнению Лапласа
и удовлетворяющая уравнению Лапласа  , называется гармонической на
, называется гармонической на 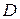 .
.
Теорема (необходимое условие аналитичности) .
Для аналитичности 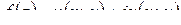 необходимо, чтобы
необходимо, чтобы 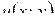 и
и 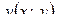 были гармоническими функциями, то есть
были гармоническими функциями, то есть  и
и  .
.
Замечание. Однако функция 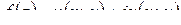 , где
, где 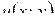 и
и 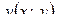 – произвольные гармонические функции на
– произвольные гармонические функции на 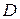 , не всегда является аналитической. Она будет аналитической, только если функции
, не всегда является аналитической. Она будет аналитической, только если функции 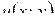 и
и 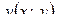 удовлетворяют на
удовлетворяют на 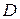 условиям Коши-Римана.
условиям Коши-Римана.
Задача 2.6. Проверить, что функция 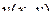 является мнимой частью аналитической функции. Восстановить аналитическую в окрестности точки
является мнимой частью аналитической функции. Восстановить аналитическую в окрестности точки 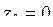 функцию
функцию 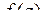 по известной мнимой части
по известной мнимой части 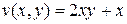 и значению
и значению  .
.
Решение
Проверим, может ли функция 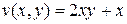 быть мнимой частью некоторой аналитической функции f(z). Для этого проверим, удовлетворяет ли она уравнению Лапласа Δu =0:
быть мнимой частью некоторой аналитической функции f(z). Для этого проверим, удовлетворяет ли она уравнению Лапласа Δu =0:
 ,
,  ,
, 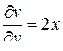 ,
, 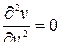 .
.
Таким образом,
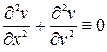 .
.
Функция 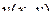 удовлетворяет уравнению Лапласа и может служить мнимой частью некоторой аналитической функции
удовлетворяет уравнению Лапласа и может служить мнимой частью некоторой аналитической функции  , а это будет так, если она ещё будет удовлетворять условиям Коши-Римана
, а это будет так, если она ещё будет удовлетворять условиям Коши-Римана
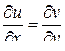 и
и 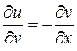 .
.
Подберём функцию u(x;y) так, чтобы условия Коши-Римана выпол-нялись:
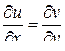
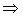
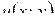
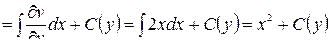 .
.
здесь константа интегрирования зависит от y как функция. Это связано с тем, что u(x ; y) зависит от двух переменных, а интегрирование ведётся только по одной переменной x и переменная y считается константой.
Замечание. Легко убедиться, что если мы конечный результат, а именно: 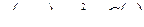 , продифференцируем по x:
, продифференцируем по x:
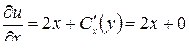
и подставим в первое условие Коши-Римана
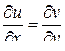 ,
,
то оно будет выполнено: 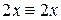 .
.
Итак, используя первое условие Коши-Римана, мы нашли неизвестную действительную часть 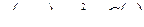 с точностью до произвольной функции
с точностью до произвольной функции 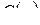 , зависящей от одной переменной y.
, зависящей от одной переменной y.
Чтобы найти эту неизвестную функцию 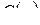 , воспользуемся вторым условием Коши-Римана:
, воспользуемся вторым условием Коши-Римана: 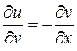 .
.
Имеем: 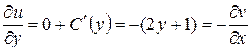 , то есть
, то есть 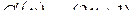 .
.
Откуда
 ,
,
где 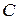 – произвольная константа интегрирования. Подставляем найденную функцию
– произвольная константа интегрирования. Подставляем найденную функцию 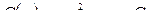 в искомую функцию
в искомую функцию  , получаем
, получаем 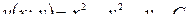 .
.
Итак, искомая аналитическая функция 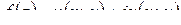 найдена.
найдена.

 .
.
Но она найдена с точностью до произвольной константы. Определим неизвестную константу 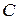 из условия
из условия  .
.
Имеем 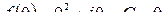 , откуда
, откуда 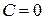 .
.
Ответ: 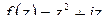 .
.
Дата: 2018-12-21, просмотров: 323.