Рядом Лорана называется ряд вида 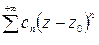 . Этот ряд понимается как сумма двух рядов:
. Этот ряд понимается как сумма двух рядов:
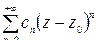 – правильная часть ряда Лорана,
– правильная часть ряда Лорана,
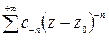 – главная часть ряда Лорана,
– главная часть ряда Лорана,
и сходящийся тогда и только тогда, когда сходятся обе его части.
Если функция f(z) аналитическая в кольце 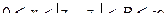 , то она представляется в этом кольце рядом Лорана:
, то она представляется в этом кольце рядом Лорана:
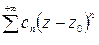 ,
,
где
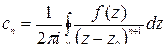 ,
, 
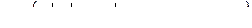 .
.
Точка z0 называется изолированной особой точкой функции f(z), если существует проколотая окрестность 
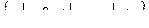 точки z0, в которой
точки z0, в которой 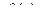 аналитична, а в самой точке z0 аналитичность нарушена.
аналитична, а в самой точке z0 аналитичность нарушена.
Изолированная особая точка z0 функции f(z) называется:
Ø устранимой, если главная часть ряда Лорана функции f(z) в 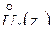 отсутствует;
отсутствует;
Ø полюсом порядка k, если главная часть ряда Лорана функции f(z) в 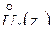 содержит конечное число (а именно: k) членов (в случае k =1 полюс называется простым);
содержит конечное число (а именно: k) членов (в случае k =1 полюс называется простым);
Ø существенно особой, если главная часть ряда Лорана функции f(z) в 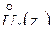 содержит бесконечное число членов.
содержит бесконечное число членов.
При определении характера изолированной особой точки использу-ются следующие теоремы.
1. Для того чтобы точка z0 являлась устранимой особой точкой аналитической функции f(z), необходимо и достаточно существование конечного предела 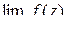 .
.
2. Для того чтобы точка z0 являлась полюсом аналитической функции f(z), необходимо и достаточно существование предела 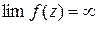 .
.
2'. Для того чтобы точка z0 являлась полюсом порядка n аналитической функции f(z), необходимо и достаточно, чтобы функцию f(z) можно было представить в виде 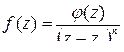 , где φ(z) – функция аналитическая в точке
, где φ(z) – функция аналитическая в точке  , причём φ(z)≠0/
, причём φ(z)≠0/
2". Пусть  – изолированная особая точка функции
– изолированная особая точка функции 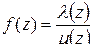 , где
, где 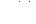 и
и 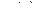 – функции аналитические в точке
– функции аналитические в точке  . Если числитель
. Если числитель 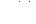 и все производные до
и все производные до 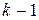 порядка включительно в точке
порядка включительно в точке  равны нулю, а
равны нулю, а 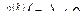 , знаменатель
, знаменатель 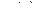 и все производные до
и все производные до 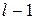 порядка включительно в точке
порядка включительно в точке  равны нулю, а
равны нулю, а 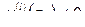 , то при
, то при 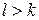 точка
точка  является полюсом порядка
является полюсом порядка 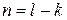 аналитической функции
аналитической функции 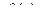 . Если
. Если 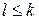 , то точка
, то точка  является устранимой особой точкой аналитической функции
является устранимой особой точкой аналитической функции 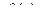 .
.
3. Пусть при 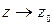 аналитическая функция
аналитическая функция 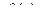 не имеет пределов ни конечного, ни бесконечного. Это условие является необходимым и достаточным для того, чтобы точка
не имеет пределов ни конечного, ни бесконечного. Это условие является необходимым и достаточным для того, чтобы точка  была существенно особой точкой функции
была существенно особой точкой функции 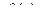 .
.
Задача 5.1. Разложить в ряд по степеням 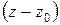 функции:
функции:
a) 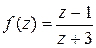 ,
,  ; б)
; б) 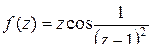 ,
,  .
.
Решение
а) функция 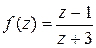 не аналитична лишь в одной точке
не аналитична лишь в одной точке 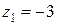 . Рассмотрим окружность
. Рассмотрим окружность  с центром в точке
с центром в точке  и проходящую через точку
и проходящую через точку 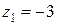 :
: 
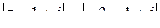
 . Эта окружность разбивает всю плоскость на две области: круг
. Эта окружность разбивает всю плоскость на две области: круг 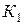 :
: 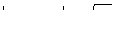 и кольцо
и кольцо 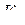 :
: 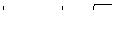 , в каждой из которых функция
, в каждой из которых функция 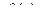 аналитична. Следовательно, в круге
аналитична. Следовательно, в круге 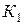 функция
функция 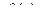 разлагается в ряд Тейлора, а в кольце
разлагается в ряд Тейлора, а в кольце 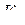 – в ряд Лорана, причём оба разложения по степеням разности
– в ряд Лорана, причём оба разложения по степеням разности 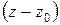 , то есть по степеням
, то есть по степеням  .
.
Преобразуем функцию  , выделяя нужную разность так, чтобы можно было воспользоваться известным разложением
, выделяя нужную разность так, чтобы можно было воспользоваться известным разложением
 ,
, 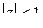 .
.
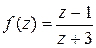
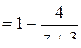
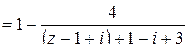
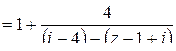
Для разложения в  вынесем в знаменателе дроби
вынесем в знаменателе дроби  число
число 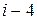 , получим:
, получим: 
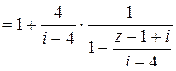 .
.
Если теперь ввести обозначение 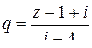 , то дробь
, то дробь 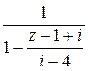 можно разложить по формуле
можно разложить по формуле 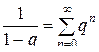 , то есть
, то есть
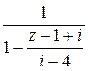 =
= 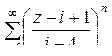 .
. 
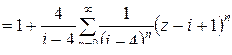 –
–
ряд Тейлора. Это разложение имеет место при
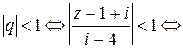
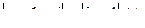
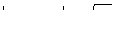 ,
,
то есть в круге 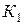 .
.
Для разложения в 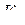 вынесем в знаменателе дроби
вынесем в знаменателе дроби 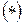 выражение
выражение 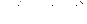 за скобки, получим:
за скобки, получим:
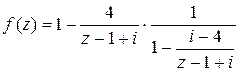
Если ввести обозначение 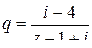 , то снова по формуле
, то снова по формуле 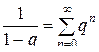 получим:
получим: 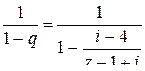 =
= 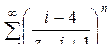 ,
,
а 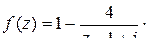
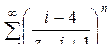 = =
= = 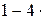
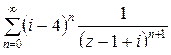 –
–
это ряд Лорана. Разложение имеет место при
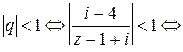
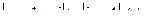
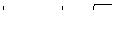 ,
,
то есть в области 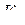 .
.
б) функцию 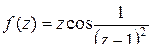 нужно разложить по степеням
нужно разложить по степеням 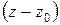 , то есть
, то есть 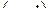 . В точке
. В точке  и только в ней функция
и только в ней функция  не аналитична, но она аналитична в кольце
не аналитична, но она аналитична в кольце 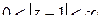 , следовательно, в этом кольце она разлагается в ряд Лорана.
, следовательно, в этом кольце она разлагается в ряд Лорана.
В выражении для  выделим разность
выделим разность 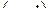 :
:
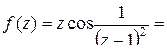
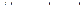
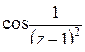
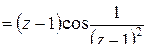
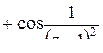 .
. 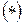
Введём обозначение  , и воспользуемся известным разложением:
, и воспользуемся известным разложением: 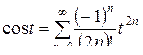 .
.
Значит, 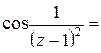
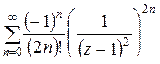
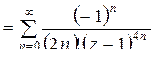 .
.
Подставим последнее разложение в 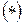 :
:

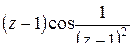
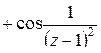

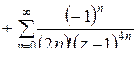 = =
= = 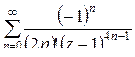
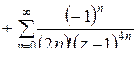 .
.
Это и есть искомое разложение в ряд Лорана. Оно имеет место на всей комплексной плоскости, кроме точки 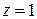 .
.
Задача 5.2
Определить типы изолированных особых точек для функции:
а) 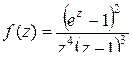 ; б)
; б) 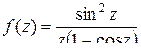 ; в)
; в) 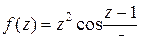 .
.
Решение
а) Функции 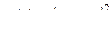 и
и  аналитичны на всей комплексной плоскости, следовательно, их частное аналитично всюду, где
аналитичны на всей комплексной плоскости, следовательно, их частное аналитично всюду, где 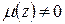 , то есть особые точки функции
, то есть особые точки функции 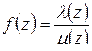 – это нули функции
– это нули функции 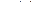 . Очевидно, функция
. Очевидно, функция  имеет нули:
имеет нули:  , кратности 4, и
, кратности 4, и  , кратности 3.
, кратности 3.
Рассмотрим изолированную особую точку  функции
функции 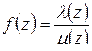 , где
, где 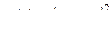 , а
, а 
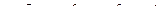 , и применим теорему 2" для определения её типа.
, и применим теорему 2" для определения её типа.
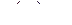 ,
,  ,
, 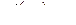 ,
, 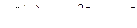 ,
,
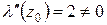 ,
,
следовательно,
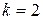 .
. 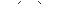 ,
, 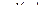
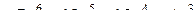 ,
, 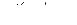 ,
,
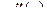
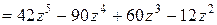 ,
, 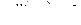 ,
,
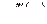
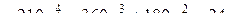 ,
, 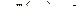 ,
,
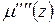
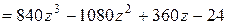 ,
,  ,
,
следовательно, 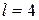 . Тогда
. Тогда  полюс порядка
полюс порядка 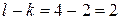 .
.
Изолированная особая точка  является полюсом второго порядка.
является полюсом второго порядка.
Рассмотрим изолированную особую точку  для функции
для функции
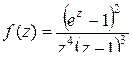
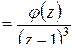 ,
,
где  – функция аналитическая в точке
– функция аналитическая в точке  , причём
, причём 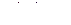 . Применяя теорему 2´ для определения типа изолированной особой точки, заключаем, что
. Применяя теорему 2´ для определения типа изолированной особой точки, заключаем, что  – полюс третьего порядка.
– полюс третьего порядка.
б) Функции 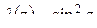 и
и 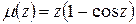 аналитичны на всей комплексной плоскости, следовательно, их частное аналитично всюду, где μ(z)≠0, то есть особые точки функции
аналитичны на всей комплексной плоскости, следовательно, их частное аналитично всюду, где μ(z)≠0, то есть особые точки функции 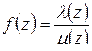 – это нули функции μ(z).
– это нули функции μ(z).
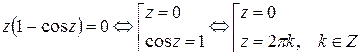 .
.
Таким образом, изолированными особыми точками функции 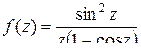 являются
являются  и
и 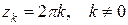 .
.
Для точки  применим теорему 2":
применим теорему 2":
 ,
,  ,
, 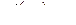 ,
, 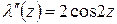 ,
,
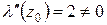 ,
,
следовательно,
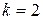 ,
, 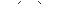 ,
,  ,
, 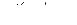 ,
,
 ,
, 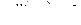 ,
,
 ,
, 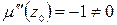 ,
,
следовательно, 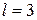 . Тогда
. Тогда  полюс порядка
полюс порядка 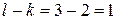 . Изолиро-ванная особая точка
. Изолиро-ванная особая точка  является полюсом первого порядка.
является полюсом первого порядка.
Для точек 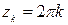 применим теорему 2":
применим теорему 2":
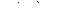 ,
, 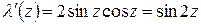 ,
, 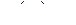 ,
, 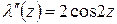 ,
,
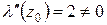 ,
,
следовательно,
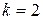 ,
, 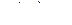 ,
,  ,
, 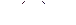 ,
,
 ,
,  ,
,
следовательно, 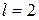 . Так как
. Так как 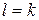 , изолированные особые точки
, изолированные особые точки 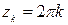 ,
, 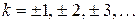 являются устранимыми особыми точками.
являются устранимыми особыми точками.
в) Функция 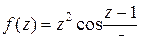 имеет одну изолированную особую точку
имеет одну изолированную особую точку  . Разложим
. Разложим  в ряд Лорана в проколотой окрестности этой точки, то есть по степеням
в ряд Лорана в проколотой окрестности этой точки, то есть по степеням 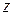 .
.
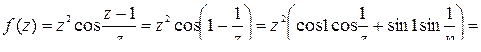
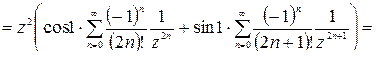
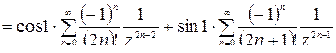
Так как ряд Лорана содержит бесконечно много отрицательных степеней, то точка  существенно особая точка для
существенно особая точка для  .
.
Дата: 2018-12-21, просмотров: 379.