Вычисление тройных интегралов в декартовых координатах.

Определение 3. Тело 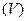 называется правильным в направлении оси Oz, если выполняются два условия:

1) Любая прямая, проходящая через внутренние точки тела  параллельно оси Oz, пересекает границу тела в двух точках;

2) Область 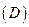, являющаяся проекцией тела  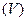на плоскость , является правильной в направлении хотя бы одной из осей координат.

Пусть тело 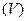 представляет собой «цилиндрический брус», ограниченный снизу и сверху, соответственно, поверхностям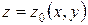и  и 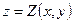, проектирующимися на плоскость  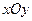в некоторую область 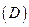, ограниченную кривой (K); с боков тело  ограничено цилиндрической поверхностью с образующими, параллельными оси Oz, и с кривой (K) в роли направляющей (рис.1.36).

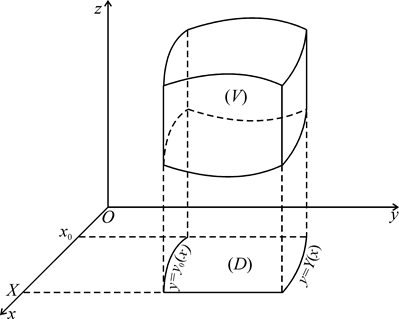
Рисунок 1.36

Теорема 3. Если дано тело , правильное в направлении оси Oz; функция трех переменных f (x, y, z) непрерывна в области , то

.

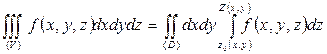Если область  представляет собой криволинейную трапецию, ограниченную двумя кривыми (рис.1.37) 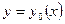 и 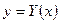 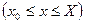и прямыми 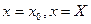, то .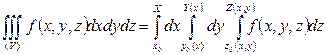

Рисунок 1.37

Пример 1. Вычислить тройной интеграл

,

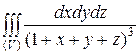где область 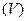 ограничена поверхностями x + y + z = 1, x = 0, y = 0, z = 0.

Решение

Уравнение 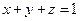 представляет собой плоскость, отсекающую на осях отрезки, равные 1; x = 0, y = 0, z = 0 – координатные плоскости. Область  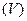есть пирамида (рис. 1.38).

Из чертежа сразу видно, что по любой из переменных можно с одинаковым успехом брать постоянные пределы, и они равны 0 и 1. Возьмем, например, постоянные пределы по 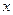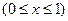. Проекцией пирамиды на плоскость  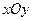является треугольник, ограниченный прямыми 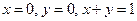. Отсюда определяем пределы интегрирования по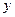 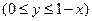. Для переменной  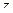нижним пределом интегрирования будет, очевидно,  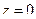(плоскость 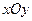), а верхним – значение 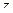, полученное из уравнения плоскости 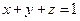, т.е. .

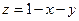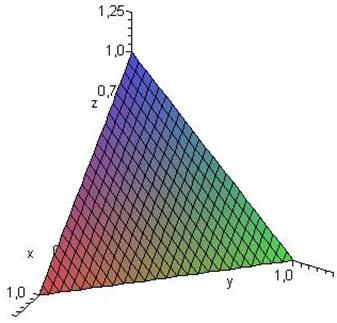
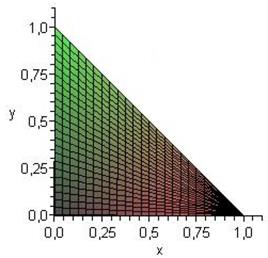
Рисунок 1.38

Определив пределы интегрирования по каждой из переменных, можем представить данный тройной интеграл через повторный и выполнить вычисления, последовательно вычисляя соответствующие определенные интегралы. Получим:

 =  =

=  =  =

=  =  =

=  =  =  – .

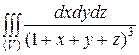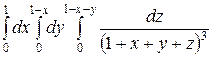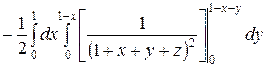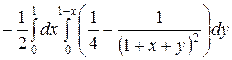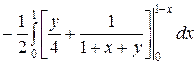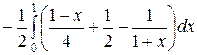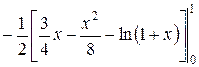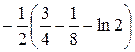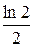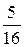Пример 2. Вычислить: 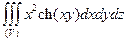, где тело (V) ограничено поверхностями x = 2, y = 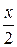, y = 0, z = 0, z = 2.

Решение

Выполним рисунок области интегрирования, ограниченной заданными в условии плоскостями (рис. 1.39). Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция области (V) на выбранную плоскость изображена на рис. 1.40. Тогда исходный интеграл сводится к повторному с пределами интегрирования (рис. 1.40) по переменной х от 0 до 2, по у от 0 до 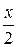, и, в соответствии с рис. 1.39, по оси z от 0 до 2.

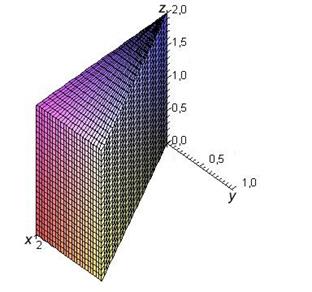
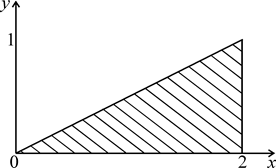
Рисунок 1.39                                           Рисунок 1.40

 =  =  =

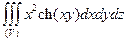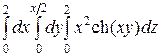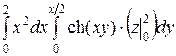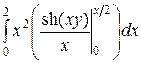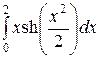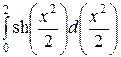= 2  = 2  = 2  = 2сh  =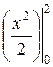

= 2(ch2 – 1).

Пример 3. Вычислить: 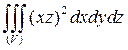, где тело (V) ограничено поверхностями x = 2, y = 2x, y = 0, z = 0, z = xy.

Решение

Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностью и плоскостями (рис. 1.41).

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция области (V) на выбранную плоскость изображена на рис. 1.42.

Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 1.41) по переменной х от 0 до 2, по у от 0 до 2x, и, в соответствии с рис. 1, по оси z от плоскости z = 0 до «седла» xy.

 =  =  =  =

=  =  =  =  = .

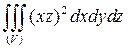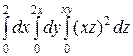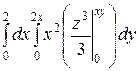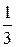
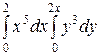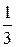
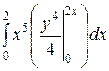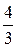
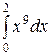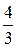
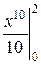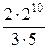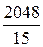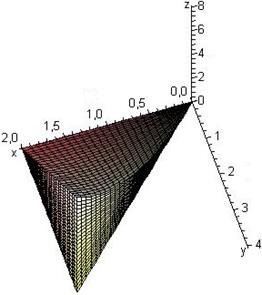
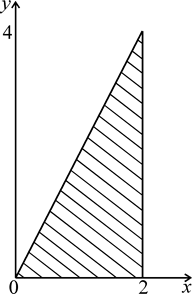
Рисунок 1.41                                           Рисунок 1.42