Рассмотрим тело (V), плотность 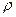 которого известна, но переменна, т.е. в разных точках различна, и предположим, что нам требуется подсчитать массу  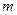этого тела. Для этого разобьем тело (V) произвольным образом на элементарные тела  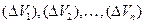соответственно с объемами  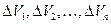и выберем в каждом из них по точке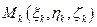 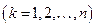. Примем приближенно, что в пределах элементарного тела  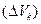плотность постоянна и равна плотности  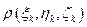в выбранной точке. Тогда масса  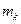каждого элементарного тела приближенно выразится следующим образом:

,

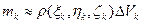масса же всего тела будет

.

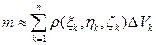   В пределе, при стремлении к нулю наибольшего из диаметров d всех областей 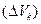, это равенство делается точным, так что

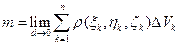                             ,                                  (2.1)

и задача решена.

       Предел этого вида и есть тройной интеграл от функции 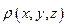 по области 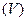. В принятых нами для них обозначениях полученный выше результат запишется так:

.

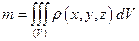Определение тройного интеграла

Возьмем произвольную фигуру 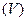 в пространстве, представляющую собой ограниченную и замкнутую область. Условие существования объема для данной области в пространстве заключается в том, чтобы область  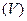была ограничена одной или несколькими гладкими поверхностями. В этом случае область (V) называют кубируемой. В дальнейшем будем рассматривать только кубируемые области пространства.

     Определение 1. Ограниченная замкнутая область пространства называется телом.

Пусть в некотором теле (V) задана функция 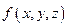. Разобьем это тело с помощью сети поверхностей на конечное число элементарных тел  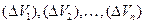соответственно с объемами 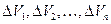. Выберем в каждом из них произвольным образом по точке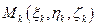 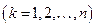. Значение функции в этой точке  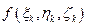умножим на объем  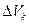 и составим интегральную сумму для функции  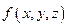по телу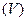

                                .                                    (2.2)

Определение 2. Конечный предел 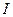 интегральной суммы (2.2) при стремлении к нулю наибольшего из диаметров d всех элементарных тел  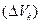называется тройным интегралом функции  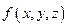в области 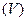, если он не зависит ни от способа разбиения тела  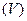на элементарные тела, ни от выбора точек M_k в каждом из них:

.

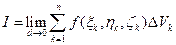Он обозначается символом .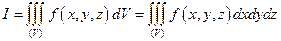

Теорема 1. (необходимое условие существования тройного интеграла). Если функция 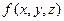 интегрируема в ограниченной замкнутой области пространства 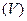, то она ограничена в этой области.

     Теорема 2. (достаточное условие существования тройного интеграла). Если функция 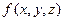  непрерывна в ограниченной замкнутой области пространства 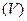, то она интегрируема в ней.

Из пункта 2.1. следует физический смысл тройного интеграла. Если функция 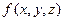 есть плотность распределения массы по телу 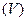, то тройной интеграл от функции  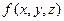в области  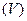равен массе этого тела:

.

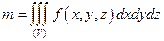Свойства тройного интеграла

1. .

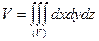2. Если умножить интегрируемую функцию в области  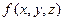на постоянную 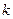, то полученная функция также будет интегрируема, и при этом

.

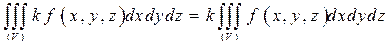3. Если в области 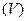 интегрируемы функци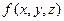и  и 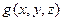, то интегрируема и функция 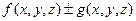, причем

.

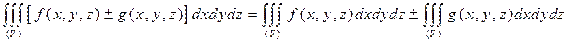4. Если в области 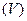 задана функция  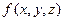и область 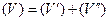, то из интегрируемости функции  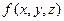во всей области  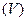следует ее интегрируемость в областях  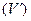и 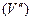, и обратно – из интегрируемости функции в обеих областях  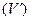и 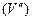 вытекает интегрируемость в области 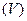. При этом

.

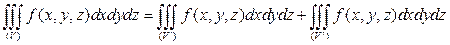5. Если для интегрируемых в области 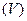 функци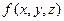й  и 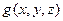 выполняется неравенств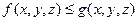о , то

.

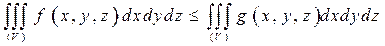6. В случае интегрируемости функции 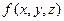 интегрируема и функция 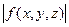, и имеет место неравенство 

.

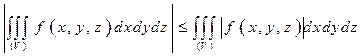7. Теорема О СРЕДНЕМ. Если функция 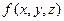 непрерывна в области 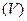, то найдется такая точка  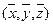в области 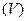, что 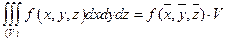, где V – объем области (V).