Рассчитаем данные коэффициенты применительно к нашему динамическому ряду, построим линейный тренд и сделаем прогноз на будущий год (табл.3.1.2).
Таблица 3.1.2
Прогнозирование товарооборота методом линейного тренда
| Года | t | t2 | Yt | Ytt | YtT | Yt – YtT |
| Первый | -2 | 4 | 91 006 | -182 012 | 136 610 | -45 604 |
| Второй | -1 | 1 | 106 113 | -106 113 | 151 647 | -45 534 |
| Третий | 0 | 0 | 122 242 | 0 | 166 685 | -44 443 |
| Четвертый | 1 | 1 | 138 500 | 138 500 | 181 722 | -43 222 |
| Пятый | 2 | 4 | 150 000 | 300 000 | 196 760 | 46 760 |
| Сумма | 0 | 10 | 607 861 | 150 375 | Ошибка, % | 38,4 |
| – | – | – | Прогноз на будущий год | 211797 | – | |
Вычислим коэффициенты линейного тренда по формулам:
а0 = ∑yt / n = 607 861/5=121 572,2;
a1 = ∑ytt / ∑t2 = 150 375/10=15 037,5
Таким образом, величина среднего уровня ряда при t = 0 составляет 12 1572,2 тыс. руб., а среднегодовое увеличение товарооборота составляет 15 037,5 тыс. руб.
Уравнение линейного тренда имеет вид: Ytт = 121 572,2 + 15 037,5х t
Прогноз объёма продаж на будущий год составит:
YtT = 121 572,2 + 15 037,5х 6 = 211 797 тыс. руб.
Для сравнения рассчитаем линейный тренд без переноса начала координат в середину ряда динамики (см. табл. 3.1.3).
a1 =∑(t-tcp) х (Yt-Ycp)/ ∑t= 150 375,0/10,0= 15 037,5
а0 = Y(t)сp – a1 х tcp = 121 572,2 – 15 037,5х3,0 = 76 459,7.
Таким образом, уравнение линейного тренда имеет вид:
YtT = 76 549,7 + 15 037,5 t
Прогноз объема продаж на будущий год составит:
YtT = 76 549,7 + 15 037,5х 6 = 166 685 тыс. руб.
Таблица 3.1.3
Прогнозирование товарооборота методом линейного тренда
| Годы | t | Y(t) | (t-tcp) | (t-tcp)2 | Yt – Yср | (t- tср)х (Yt – Yср) | Расчёт Yр(t) | Откло-нение Е(t) | | Yt – YtT| х 100/ Yt |
| Первый | 1 | 91 006 | -2,0 | 4,0 | -30566 | 61132,4 | 91497 | -491,2 | 0,540 |
| Второй | 2 | 106 113 | -1,0 | 1,0 | -15459 | 15459,2 | 106535 | -421,7 | 0,397 |
| Третий | 3 | 122 242 | 0,0 | 0,0 | 670 | 0,0 | 121572 | 669,8 | 0,548 |
| Четвертый | 4 | 138 500 | 1,0 | 1,0 | 16928 | 16927,8 | 136610 | 1890,3 | 1,365 |
| Пятый | 5 | 150 000 | 2,0 | 4,0 | 28428 | 56855,6 | 151647 | -1647,2 | 1,098 |
| Сумма | 15 | 607 861 | 0,0 | 10,0 | 0,0 | 150375,0 | – | – | 3,948 |
| Средняя величина | 3,0 | 121572,2 | – | – | – | Прогноз на будущий год | 166685 | величина ошибки, % | 0,79 |
Как видно из таблицы, данный расчёт более трудоёмок, однако даёт меньшую сумму отклонений (3,948 %) и более приближенное к реальному прогнозное значение. Среднелинейная ошибка составляет 0,79 %, что говорит о том, что с вероятностью 99,21 % прогнозный объём продаж товаров в будущем году составит 166 685 тыс. руб.
Однако есть еще один вариант расчёта прогнозной модели показателя с помощью полинома первой степени – линейный тренд, рассчитанный по базисным темпам роста, без переноса начала координат. Данный метод обычно используется при анализе временных рядов с целью получения «кривой освоения» на товарном рынке.
На основе фактических данных о товарообороте предприятия составим основную тенденцию определения объёма продаж товаров или так называемую «кривую освоения», начиная с первого года, по данным, представленным в табл. 3.1.1 в строке 2.
Под основной тенденцией понимается некоторое общее направление развития исследуемого явления, которое определяется на основе выравнивания временного ряда по методу наименьших квадратов и сводится к представлению в виде плавной линии, выраженной функцией:
Yt = f(t)+Et.
Для дальнейших расчётов преобразуем абсолютные значения объема товарооборота в относительные значения, приняв товарооборот первого года за 100 % (см. табл. 3.1.1).
Допустим, что основная тенденция описывается линейной функцией:
Yt=a+bt.
Для нахождения параметров необходимо решить следующую систему уравнений:
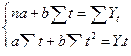
Для решения системы уравнения заполним табл. 3.1.4.
Таблица 3.1.4
Матрица параметров математических функций
| Год | Yt | t | t2 | Yt t | YtT | Yt – YtT | ( Yt – YtT)2 | | Yt – YtT| х 100/ Yt |
| Первый | 100,0 | 1 | 1 | 100,0 | 100,5 | -0,5 | 0,3 | 0,5 |
| Второй | 116,6 | 2 | 4 | 233,2 | 117,1 | -0,4 | 0,2 | 0,4 |
| Третий | 134,3 | 3 | 9 | 403,0 | 133,6 | 0,7 | 0,6 | 0,6 |
| Четвертый | 152,2 | 4 | 16 | 608,8 | 150,1 | 2,1 | 4,3 | 1,4 |
| Пятый | 164,8 | 5 | 25 | 824,1 | 166,6 | -1,8 | 3,3 | 1,1 |
| Сумма | 667,9 | 15 | 55 | 2169,0 | – | – | 8,6 | 3,9 |
Рассчитав первые 4 столбца, подставим значения в систему:
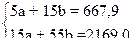
Решение системы даст искомые значения а = 83,99 и b = 16,53.
Следовательно, линейная функция Yt будет иметь вид:
Yt = 83,99+16,53t.
Для нахождения величины среднелинейной ошибки Е вычислим значение Yt теоретическое путём последовательной подстановки значения t от 1 до 6. После этого рассчитаем значение граф 7, 8 и 9.
Е=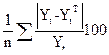 
=3,926/5 = 0,785%.
Дата: 2018-12-21, просмотров: 384.
