Использование функции рабочего листа ТЕНДЕНЦИЯ – это самый простой способ вычисления регрессионного анализа. Предположим, результаты наших наблюдений внесены в ячейки А2:А6, а года расположены в ячейках В2:В6. Выделим ячейки С2:С6 и введем следующую формулу, используя формулу массива: =ТЕНДЕНЦИЯ (А2: А6; В2: В6)
Получим результат, показанный в табл. 3.1.10.
Таблица 3.1.10
Прогнозирование товарооборота с помощью функции ТЕНДЕНЦИЯ, тыс. руб.
| Год | Фактический объём продаж | Прогнозный объём |
| Первый | 91 006 | – |
| Второй | 106 113 | 91 006 |
| Третий | 122 242 | 121 220 |
| Четвертый | 138 500 | 137 690 |
| Пятый | 150 000 | 154 118 |
| Шестой | – | 166 685 |
Формула фактически говорит о следующем: "Если известно, каким образом у-значения в диапазоне В1:В5 соотносятся с х-значениями в диапазоне А1:А5, то какой результат у-значения мы получим, зная новое х-значение временного момента, равное 6" Полученное значение 166 685 тыс.руб. является прогнозом на основе фактических данных на пока еще не наступивший шестой временной отсчет.
Однако есть и другие встроенные функции Excel, также применяемые для составления прогнозов для линейных динамических рядов. В частности, функции ПРЕДСКАЗ и ЛИНЕЙН. Полученные с их помощью прогнозные значения объёмов продаж в нашем случае аналогичны прогнозам, рассчитанным посредством функции ТЕНДЕНЦИЯ.
Функция ПРЕДСКАЗ вычисляет или предсказывает будущее значение по существующим значениям. Предсказываемое значение – это у-значение, соответствующее заданному х-значению. Известные значения – это х- и у-значения, а новое значение предсказывается с использованием линейной регрессии. Эту функцию можно использовать для предсказания будущих продаж, потребностей в оборудовании или тенденций потребления.
Уравнение для ПРЕДСКАЗ имеет вид а+bx, где
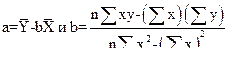 .
.
В Excel функция выглядит следующим образом: ПРЕДСКАЗ(х;известные_значения_у;известные_значения_х),
где х – это точка данных, для которой предсказывается значение;
известные_значения_у – это зависимый массив или интервал данных;
известные_значения_х – это независимый массив или интервал данных.
Получим результат, показанный в табл. 3.1.11.
Таблица 3.1.11
Прогнозирование товарооборота с помощью функции ПРЕДСКАЗ, тыс.руб.
| Годы | Фактический объём продаж | Прогнозный объём |
| Первый | 91 006 | – |
| Второй | 106 113 | – |
| Третий | 122 242 | 121 220 |
| Четвертый | 138 500 | 137 690 |
| Пятый | 150 000 | 154 118 |
| Шестой | – | 166 685 |
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива.
Уравнение для прямой линии имеет следующий вид:
у = mx + b или
у = mlxl + m2x2 + ... + b (в случае нескольких диапазонов значений х),
где зависимое значение у функция независимого значения х; значения m коэффициенты, соответствующие каждой независимой переменной х; b – постоянная.
Результаты функции ЛИНЕЙН аналогичны результатам функции ПРЕДСКАЗ.
Функция ТЕНДЕНЦИЯ вычисляет прогнозы, основанные на линейной связи между результатом наблюдения и временем, когда это наблюдение было зафиксировано. Предположим, что вы составляете линейный график данных, на вертикальной оси которого отмечаете результаты наблюдений, а на горизонтальной фиксируете временные моменты их получения. Если эта взаимосвязь носит линейный характер, то линия на графике будет либо прямой, либо слегка наклоненной в одну или другую сторону, либо горизонтальной. Это и будет лучшей подсказкой о том, что взаимосвязь является линейной, и потому в данном случае функция ТЕНДЕНЦИЯ – самый удобный способ регрессивного анализа.
Однако если линия резко изгибается в одном из направлений, то это означает, что взаимосвязь показателей носит нелинейный характер. Существует большое количество типов данных, которые изменяются во времени нелинейным способом. Некоторыми примерами таких данных являются объём продаж новой продукции, прирост населения, выплаты по основному кредиту и коэффициент удельной прибыли. В случае нелинейной взаимосвязи функция Excel РОСТ поможет вам получить более точную картину направления развития вашего бизнеса, чем функция ТЕНДЕНЦИЯ.
Как и при использовании функции ТЕНДЕНЦИЯ, пользователь в данном случае может генерировать прогнозы, просто подставляя новые значения х (табл.3.1.12).
Прогнозное значение объема продаж на шестой год, полученное с помощью функции РОСТ, составило 174 919 тыс. руб., что на 5 % выше значения, рассчитанного по другой функции регрессии.
Таблица 3.1.12
Прогнозирование товарооборота с помощью функции РОСТ, тыс. руб.
| Год | Фактический объём продаж | Прогнозный объём |
| Первый | 91 006 | – |
| Второй | 106 113 | 91 006 |
| Третий | 122 242 | 123 728 |
| Четвертый | 138 500 | 141 961 |
| Пятый | 150 000 | 160 518 |
| Шестой | – | 174 919 |
Значения, предсказанные с помощью функции ТЕНДЕНЦИЯ, очень близки к реальным, а линия ТЕНДЕНЦИЯ гораздо лучше описывает первых пять наблюдений, полученных в действительности, чем линия РОСТ. Следовательно, для этой базовой линии более вероятно точное прогнозирование последующих данных с использованием функции ТЕНДЕНЦИЯ, а не РОСТ. Использование функции ТЕНДЕНЦИЯ свидетельствует о том, что базовая линия является линейной.
Дата: 2018-12-21, просмотров: 848.