Для лучшего отображения особенностей изменения исследуемого показателя на конце периода наблюдения целесообразно использовать адаптивные модели, каждая из которых имеет определённый механизм приспособления к новым условиям. Общим для всех моделей этой группы является придание наибольшего веса последним наблюдениям при оценке параметров.
Все адаптивные модели базируются на двух схемах: скользящего среднего (СС-модели) и авторегрессии (АР-модели).
Согласно схеме скользящего среднего, оценкой текущего уровня является взвешенное среднее всех предшествующих уровней, причём веса при наблюдениях убывают по мере удаления от последнего уровня, т.е. информационная ценность наблюдений признается тем большей, чем ближе находятся они к концу интервала наблюдений. Такие модели более точно отражают изменения, происходящие в тенденции, но не позволяют в чистом виде отражать колебания.
В авторегрессионной схеме оценкой текущего уровня является взвешенная сумма не всех, а нескольких предшествующих уровней; при этом весовые коэффициенты при наблюдениях не ранжированы. Информационная ценность наблюдений определяется не их близостью к моделируемому уровню, а теснотой связи между ними.
В практике статистического прогнозирования наиболее часто используются две базовые СС-модели: Брауна и Хольта, первая из которых является частным случаем второй. Эти модели представляют процесс развития как линейную тенденцию с постоянно изменяющимися параметрами. Прогнозная оценка Yp(t,k) уровня ряда Y(t+k), вычисляются в момент времени t на k шагов вперед:
Yp (t,k) = A0(t) + A1(t) 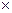 k
k
где A0(t) – оценка текущего (t -го) уровня;
A1(t) – оценка текущего прироста.
Далее определяется величина их расхождения (ошибки). При k=l имеем:
e(t+l) = Y(t+l)-Yp(t,l).
В соответствии с этой величиной корректируются параметры модели. В модели Брауна модификация осуществляется следующим образом:
A0(t) – A 0(t-l) +Al(t-l) + (1-  2)
2) 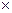 e(t);
e(t);
A1(t)=A1(t-l) + (l-  )2
)2 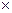 e(t).
e(t).
где  – коэффициент дисконтирования данных, изменяющийся в пределах от 0 до 1;
– коэффициент дисконтирования данных, изменяющийся в пределах от 0 до 1;
а – коэффициент сглаживания (а = 1 -  );
);
e (t) ошибка прогнозирования уровня Y(t), вычисленная в момент времени (t-1) на один шаг вперед.
В модели Хольта коэффициенты модифицируются следующим образом:
A0(t) = A0(t-l) +A1(t-l) + 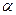 1
1 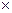 e(t);
e(t);
A1(t) = A1(t-l) + 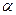 1
1 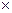
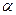 2
2 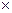 e(t);
e(t);
где 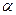 1,
1, 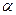 2 – коэффициенты сглаживания (адаптации), изменяющиеся в пределах от 0 до 1.
2 – коэффициенты сглаживания (адаптации), изменяющиеся в пределах от 0 до 1.
Параметры вычисляются последовательно, от уровня к уровню, и их значения для последнего уровня определяют окончательный вид модели. Начальные значения параметров оцениваются на основе нескольких (например, пяти) первых уровней ряда.
Коэффициент А0 – значение, близкое к последнему уровню, и представляет как бы закономерную составляющую этого уровня.
Коэффициент А1 – определяет прирост, сформировавшийся в основном к концу периода наблюдений, но отражающий также (правда, в меньшей степени) скорость роста и на более ранних этапах.
Для исследования динамики развития товарооборота на анализируемом предприятии воспользуемся моделью Брауна. Как уже говорилось выше, расчётное значение в момент времени t получается по формуле
Yp(t) = a0 (t-l)+ a1 (t-l)k (t = 1,2,...,N),
k – количество шагов прогнозирования (обычно k=l),
Это значение сравнивается с фактическим уровнем, и полученная ошибка прогноза E(t) = Y(t)-Yp(t) используется для корректировки модели. Корректировка параметров осуществляется по формулам
a0(t)= a0(t-l)+a1(t-l)+E(t)(l-  2)
2)
a1(t)= a1(t-l)+ E(t)(l-  2),
2),
где  – коэффициент дисконтирования данных, отражающий большую степень доверия к более поздним данным. Его значение должно быть в интервале от 0 до 1.
– коэффициент дисконтирования данных, отражающий большую степень доверия к более поздним данным. Его значение должно быть в интервале от 0 до 1.
Такой процесс модификации модели в зависимости от ее текущих прогнозных качеств обеспечивает адаптацию к новым закономерностям развития.
Модель Брауна может отображать развитие не только в виде линейной тенденции, но в виде случайного процесса, не имеющего тенденции, а также в виде параболической тенденции. Соответственно различают модели Брауна:
• нулевого порядка, которая описывает процессы, не имеющие тенденции развития: она располагает лишь одним параметром А0 (оценка текущего уровня). Прогноз развития на k шагов вперед осуществляется согласно формуле y(t+k)=A0. Такая модель еще называется «наивной» («будет, как было»);
• первого порядка;
• второго порядка, отражающей развитие в виде параболической тенденции с изменяющимися скоростью и ускорением. Она имеет три параметра (А2 – оценка текущего прироста или ускорение). Прогноз осуществляется по формуле: y(t+k) = А0 + A1k + A2k2.
Для исследования динамики развития товарооборота и составления его прогнозной модели на анализируемом предприятии воспользуемся моделью Брауна первого порядка (см. табл. 3.1.8).
Таблица 3.1.8
Оценка параметров модели Брауна
| Год | t | Y(t) | (t-tср) | (t-tср)2 | Yt-Yсp | (t-tср) 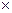 (Yt-Yсp) (Yt-Yсp)
| a0 | a1 | Yрасч | Откло-нение | |Yt – YtТ|  Yt Yt
|
| 0 | 76460 | 15037,5 | |||||||||
| Первый | 1 | 91 006 | -2,0 | 4,0 | -30566 | 61132,4 | 91182,8 | 14958,9 | 91 497 | -491,2 | 0,540 |
| Второй | 2 | 106 113 | -1,0 | 1,0 | -15459 | 15459,2 | 106123,3 | 14954,3 | 106 142 | -28,7 | 0,027 |
| Третий | 3 | 122 242 | 0 | 0 | 670 | 0 | 121822,8 | 15140,6 | 121 078 | 1164,3 | 0,952 |
| Четвертый | 4 | 138 500 | 1,0 | 1,0 | 16928 | 16927,8 | 137946,8 | 15386,5 | 136 963 | 1536,6 | 1,109 |
| Пятый | 5 | 150 000 | 2,0 | 4,0 | 28428 | 56855,6 | 151200 | 14853,1 | 153 333 | -3333,3 | 2,222 |
| Сумма | 15 | 607 861 | 0,0 | 10,0 | 0 | 150375 | прогноз на будущий год | 166 053 | - | 4,851 | |
| Средняя величина | 3 | 121 572,2 | - | - | - | - | Величина ошибки, % | - | 0,97 | ||
Используя данные таблицы, получим:
Ycp= 121 572,2
tсp = 3,0
а1(0)=15 037,5;
а0(0)= 7 6460
Примем k-1 и  =0,6 и рассчитаем прогнозные значения.
=0,6 и рассчитаем прогнозные значения.
Таким образом, прогнозное значение величины объема продаж в будущем году с вероятностью 97 % составит 166 053 тыс. руб.
Вообще АР– модели не предназначены для описания процессов с тенденцией, однако они достаточно точно описывают колебания, что весьма важно для отображения развития неустойчивых показателей. Ряды без тенденции, как правило, не представляют интереса для экономистов.
Для прогнозирования могут использоваться и другие функции, однако следует придерживаться правила: выбирать не ту функцию, которая дает наименьший коэффициент аппроксимации и наибольшую корреляцию, а ту, которую легче интерпретировать в терминах экономики. Например, если экспоненциальная функция дает коэффициент аппроксимации 0,14, а функция прямой – 0,15, то следует все же использовать для прогнозирования последнюю.
Дата: 2018-12-21, просмотров: 631.