5.1 Методические указания
Корреляционная связь (частный случай стохастической) – связь, проявляющаяся при достаточно большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и признаками-факторами.
Задача корреляционного анализа – измерение тесноты связи между варьируемыми признаками и оценка факторов, оказывающих наибольшее влияние.
Задача регрессионного анализа – выбор типа модели (формы связи), устанавливающих степени влияния независимых переменных.
Связь признаков проявляется в их согласованной вариации, при этом одни признаки выступают как факторные, а другие – как результативные. Причинно-следственная связь факторных и результативных признаков характеризуется по степени:
· тесноты;
· направлению;
· аналитическому выражению.
Регрессионный анализ
Для оценки параметров уравнений регрессии наиболее часто используется метод наименьших квадратов (МНК), суть которого заключается в следующем требовании: искомые теоретические значения результативного признака  должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических (фактических) значений, т.е.
должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических (фактических) значений, т.е.
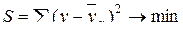 . (5.1)
. (5.1)
При изучении связей показателей применяются различного вида уравнения прямолинейной и криволинейной связи. Так, при анализе прямолинейной зависимости применяется уравнение:
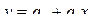 (5.2)
(5.2)
Это наиболее часто используемая форма связи между коррелируемыми признаками, при парной корреляции она выражается уравнением (6.2), где а0 – среднее значение в точке x=0, поэтому экономической интерпретации коэффициента нет; а1 – коэффициент регрессии, показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
При криволинейной зависимости применяется ряд математических функций:
полулогарифмическая 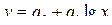 (5.3)
(5.3)
показательная 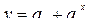 (5.4)
(5.4)
степенная  (5.5)
(5.5)
параболическая 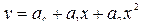 (5.6)
(5.6)
гиперболическая 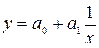 (5.7)
(5.7)
Система нормальных уравнений МНК для линейной парной регрессии имеет следующий вид:
 (5.8)
(5.8)
Отсюда можно выразить коэффициенты регрессии:
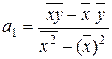 ;
;
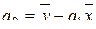 . (5.9)
. (5.9)
При численности объектов анализа до 30 единиц возникает необходимость проверить, насколько вычисленные параметры типичны для отображаемого комплекса условий, не являются ли полученные значения параметров результатом действия случайных причин. Значимость коэффициентов регрессии применительно к совокупности n<30 определяется с помощью t -критерия Стьюдента. При этом вычисляются фактические значения t -критерия:
для параметра а0: 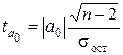 , (5.10)
, (5.10)
для параметра а1: 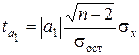 . (5.11)
. (5.11)
В формулах (5.10) и (5.11):
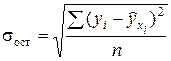 – среднее квадратическое отклонение результативного признака
– среднее квадратическое отклонение результативного признака 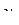 от выровненных значений
от выровненных значений 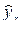 . (5.12)
. (5.12)
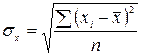 – среднее квадратическое отклонение факторного признака
– среднее квадратическое отклонение факторного признака 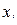 от общей средней
от общей средней  . (5.13)
. (5.13)
Полученные по формулам (5.10) и (5.11) фактические значения 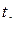 и
и 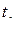 сравниваются с критическим
сравниваются с критическим 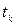 , который получают по таблице Стьюдента с учетом принятого уровня значимости
, который получают по таблице Стьюдента с учетом принятого уровня значимости 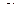 и числа степеней свободы ν (ν= n - k -1, где n – число наблюдений, k – число факторов, включенных в уравнение регрессии). Рассчитанные параметры а0 и а1 уравнения регрессии признаются типичными, если t фактическое больше t критического.
и числа степеней свободы ν (ν= n - k -1, где n – число наблюдений, k – число факторов, включенных в уравнение регрессии). Рассчитанные параметры а0 и а1 уравнения регрессии признаются типичными, если t фактическое больше t критического.
На практике часто приходится исследовать зависимость результативного признака от нескольких факторных признаков. Аналитическая форма связи результативного признака от ряда факторных признаков выражается и называется много факторным (множественным) уравнением регрессии.
Линейное уравнение множественной регрессии
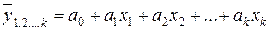 . (5.14)
. (5.14)
Система нормальных линейных уравнений МНК для оценки коэффициентов двухфакторной регрессии 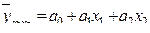 имеет вид:
имеет вид:
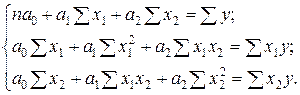 (5.15)
(5.15)
Корреляционный анализ
Различают:
- парную корреляцию – это зависимость между результативным и факторным признаком;
- частную корреляцию – это зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков;
- множественную – многофакторное влияние в статической модели
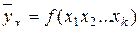 .
.
Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции (коэффициента Пирсона), который рассчитывается по одной из формул:
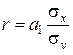 (5.16)
(5.16)
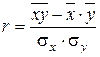 . (5.17)
. (5.17)
или 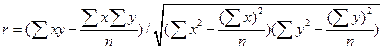
Оценка линейного коэффициента корреляции
| Значение r | Характер связи | Интерпретация связи |
| r = 0 | Отсутствует | Изменение x не влияет на изменения y |
| 0 < r < 1 | Прямая | С увеличением x увеличивается y |
| -1 > r > 0 | Обратная | С увеличением x уменьшается y и наоборот |
| r = 1 | Функциональная | Каждому значению факторного признака строго соответствует одно значение результативного |
Значимость линейного коэффициента корреляции проверяется на основе t -критерия Стьюдента. Для этого определяется фактическое значение критерия 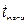 :
:
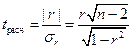 , (5.18)
, (5.18)
Вычисленное по формуле (5.18) значение 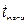 сравнивается с критическим
сравнивается с критическим 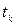 , который получают по таблице Стьюдента с учетом принятого уровня значимости
, который получают по таблице Стьюдента с учетом принятого уровня значимости 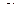 и числа степеней свободы ν. Коэффициент корреляции считается статистически значимым, если tрасч превышает
и числа степеней свободы ν. Коэффициент корреляции считается статистически значимым, если tрасч превышает 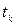 : tрасч >
: tрасч > 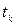 .
.
Универсальным показателем тесноты связи является теоретическое корреляционное отношение:
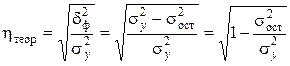 , (5.19)
, (5.19)
где 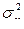 – общая дисперсия эмпирических значений y, характеризует вариацию результативного признака за счет всех факторов, включая х;
– общая дисперсия эмпирических значений y, характеризует вариацию результативного признака за счет всех факторов, включая х;
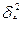 – факторная дисперсия теоретических значений результативного признака, отражает влияние фактора х на вариацию у;
– факторная дисперсия теоретических значений результативного признака, отражает влияние фактора х на вариацию у;
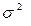 – остаточная дисперсия эмпирических значений результативного признака, отражает влияние на вариацию у всех остальных факторов кроме х.
– остаточная дисперсия эмпирических значений результативного признака, отражает влияние на вариацию у всех остальных факторов кроме х.
По правилу сложения дисперсий:
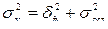 , т.е.
, т.е. 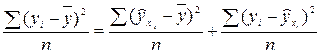 . (5.19)
. (5.19)
Оценка связи на основе теоретического корреляционного отношения (шкала Чеддока) определяется по Табл.3.3. Для линейной зависимости теоретическое корреляционное отношение тождественно линейному коэффициенту корреляции, т.е. η = |r |.
Множественный коэффициент корреляции в случае зависимости результативного признака от двух факторов вычисляется по формуле:
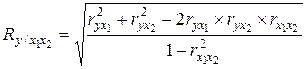 , (5.20)
, (5.20)
где 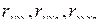 – парные коэффициенты корреляции между признаками.
– парные коэффициенты корреляции между признаками.
Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен:  .
.
| Условие включения факторных признаков в регрессионную модель – наличие тесной связи между результативным и факторными признаками и как можно менее существенная связь между факторными признаками. |
Значимость коэффициента множественной детерминации, а соответственно и адекватность всей модели и правильность выбора формы связи можно проверить с помощью критерия Фишера:
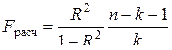 , (5.21)
, (5.21)
где R2 – коэффициент множественной детерминации (R2 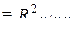 );
);
k – число факторных признаков, включенных в уравнение регрессии.
Связь считается существенной, если Fрасч > Fтабл – табличного значения F -критерия для заданного уровня значимости α и числе степеней свободы ν1 = k, ν2 = n – k – 1.
Частные коэффициенты корреляции характеризуют степень тесноты связи результативного признака и фактора, при элиминировании его взаимосвязи с остальными факторами, включенными в анализ. Расчет частных коэффициентов корреляции в случае двухфакторной регрессии (в первом случае исключено влияние факторного признака х2, во втором – х1):
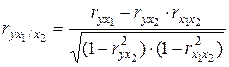 ;
; 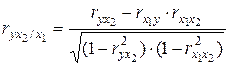 , (5.22)
, (5.22)
где r – парные коэффициенты корреляции между указанными в индексе переменными.
Для оценки сравнительной силы влияния факторов, по каждому фактору рассчитывают частные коэффициенты эластичности:
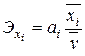 , (5.23)
, (5.23)
где 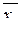 – среднее значение соответствующего факторного признака;
– среднее значение соответствующего факторного признака;
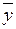 – среднее значение результативного признака;
– среднее значение результативного признака;
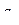 – коэффициент регрессии при i-м факторном признаке.
– коэффициент регрессии при i-м факторном признаке.
Данный коэффициент показывает, на сколько процентов следует ожидать изменения результативного показателя при изменении фактора на 1% и неизменном значении других факторов.
Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется вариацией i-го признака, входящего в множественное уравнение регрессии, рассчитывается по формуле:
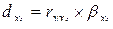 , (5.24)
, (5.24)
где 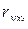 – парный коэффициент корреляции между результативным и i-м факторным признаком;
– парный коэффициент корреляции между результативным и i-м факторным признаком;
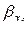 – соответствующий стандартизованный коэффициент уравнения множественной регрессии:
– соответствующий стандартизованный коэффициент уравнения множественной регрессии:
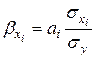 . (5.25)
. (5.25)
Показатель корреляции рангов – один из простых показателей тесноты корреляционной зависимости. Показатель рассчитывается по формуле:
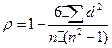 (5.26)
(5.26)
Проанализируем показатель корреляции рангов.
1. Связь полная и прямая: 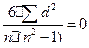 и
и 
2. Связь полная и обратная: 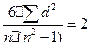 и
и 
3. Все остальные значения лежат между -1 и +1
5.2 Пример решения задач
Тема: расчет коэффициентов парной корреляции
ЗАДАЧА 87
По данным о стоимости основных производственных фондов (СОПФ) и объеме валовой продукции (ВП) определить линейное уравнение связи.
| Номер предприятия | СОПФ ( 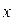 ), млн. руб. ), млн. руб.
| ВП (y), млн. руб. |
| 1 | 1 | 20 |
| 2 | 2 | 25 |
| 3 | 3 | 31 |
| 4 | 4 | 31 |
| 5 | 5 | 40 |
| 6 | 6 | 56 |
| 7 | 7 | 52 |
| 8 | 8 | 60 |
| 9 | 9 | 60 |
| 10 | 10 | 70 |
Решение.
Построим точечную диаграмму для визуального отображения зависимости объема выпуска продукции от величины основного фонда Рис.5.1.
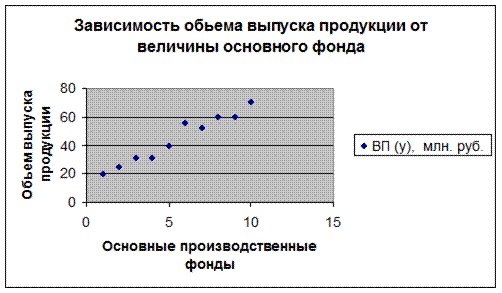
Рис.5.1 Точечная диаграмма
Создадим вспомогательную таблицу для расчета необходимых коэффициентов:
| Номер предприятия | СОПФ (  ), млн. руб. ), млн. руб.
| ВП (y), млн. руб. |  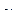
|  2 2
| 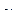 2 2
| 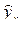
|
|
|
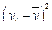
|
| 1 | 1 | 20 | 20 | 1 | 400 | 19,4 | 0,36 | 20,25 | 600,25 |
| 2 | 2 | 25 | 50 | 4 | 625 | 25 | 0 | 12,25 | 380,25 |
| 3 | 3 | 31 | 93 | 9 | 961 | 30,6 | 0,16 | 6,25 | 182,25 |
| 4 | 4 | 31 | 124 | 16 | 961 | 36,2 | 27,04 | 2,25 | 182,25 |
| 5 | 5 | 40 | 200 | 25 | 1600 | 41,8 | 3,24 | 0,25 | 20,25 |
| 6 | 6 | 56 | 336 | 36 | 3136 | 47,4 | 73,96 | 0,25 | 132,25 |
| 7 | 7 | 52 | 364 | 49 | 2704 | 53 | 1 | 2,25 | 56,25 |
| 8 | 8 | 60 | 480 | 64 | 3600 | 58,6 | 1,96 | 6,25 | 240,25 |
| 9 | 9 | 60 | 540 | 81 | 3600 | 64,2 | 17,64 | 12,25 | 240,25 |
| 10 | 10 | 70 | 700 | 100 | 4900 | 69,8 | 0,04 | 20,25 | 650,25 |
| Сумма | 55 | 445 | 2907 | 385 | 22487 | 445 | 125,4 | 82,5 | 2684,5 |
| Среднее | 5,5 | 44,5 | 290,7 | 38,5 | 2248,7 | 44,5 |
|
| 268,45 |
По формуле 5.8 составим систему уравнений:
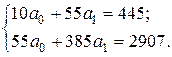 откуда вычислим коэффициенты линейного уравнения:
откуда вычислим коэффициенты линейного уравнения:
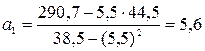 ;
;
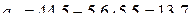 .
.
Тогда уравнение регрессии примет вид:
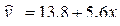 .
.
Следовательно, с увеличением стоимости основных фондов на 1 млн.руб. объем валовой продукции увеличивается в среднем на 5,6 млн. руб.
Проверим значимость полученных коэффициентов регрессии. Рассчитаем 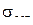 и
и 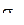 по формулам 5.12 и 5.13:
по формулам 5.12 и 5.13:
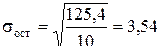
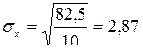
формула 5.10 для параметра а0: 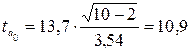
формула 5.11 для параметра а1: 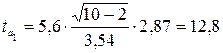 .
.
По таблице Стьюдента с учетом уровня значимости 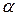 =5% и числа степеней свободы ν =10-1-1=8 получаем
=5% и числа степеней свободы ν =10-1-1=8 получаем 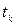 =2,306.
=2,306.
Фактические значения 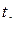 и
и 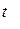 превышают табличное критическое значение
превышают табличное критическое значение 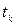 . Это позволяет признать вычисленные коэффициенты регрессии типичными.
. Это позволяет признать вычисленные коэффициенты регрессии типичными.
Рассчитаем линейный коэффициент корреляции Пирсона по формуле 5.16:
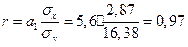 где
где 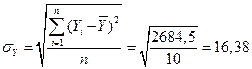
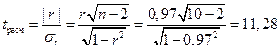
По таблице Стьюдента с учетом уровня значимости 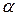 =5% и числа степеней свободы ν =10-1-1=8 получаем
=5% и числа степеней свободы ν =10-1-1=8 получаем 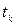 =2,306.
=2,306.
Фактическое значения 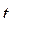 превышают табличное критическое значение
превышают табличное критическое значение 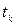 . Это позволяет признать вычисленный коэффициент корреляции типичным.
. Это позволяет признать вычисленный коэффициент корреляции типичным.
Тема: расчет множественной корреляции
ЗАДАЧА 88
Имеются некоторые данные о среднегодовой стоимости ОПФ (СОПФ), уровне затрат на реализацию продукции (ЗРП) и стоимости реализованной продукции (РП). Считая зависимость между этими показателями линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели.
| СОПФ (х1), млн.руб. | ЗРП (х2), в % к РП | РП (y), млн.руб. | 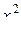
| 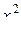
| х1 х2 | х1 y | х2 y | 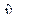
|
| 3 | 4 | 20 | 9 | 16 | 12 | 60 | 80 | 20,36 |
| 3 | 3 | 25 | 9 | 9 | 9 | 75 | 75 | 20,05 |
| 5 | 3 | 20 | 25 | 9 | 15 | 100 | 60 | 24,21 |
| 6 | 5 | 30 | 36 | 25 | 30 | 180 | 150 | 26,91 |
| 7 | 10 | 32 | 49 | 100 | 70 | 224 | 320 | 30,54 |
| 6 | 12 | 25 | 36 | 144 | 72 | 150 | 300 | 29,08 |
| 8 | 12 | 29 | 64 | 144 | 96 | 232 | 348 | 33,24 |
| 9 | 11 | 37 | 81 | 121 | 99 | 333 | 407 | 35,01 |
| 9 | 15 | 36 | 81 | 225 | 135 | 324 | 540 | 36,25 |
| 10 | 15 | 40 | 100 | 225 | 150 | 400 | 600 | 38,33 |
| S = 66 | S = 90 | S = 294 | S = 490 | S = 1018 | S = 688 | S = 2078 | S = 2880 | S = 294 |
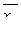 =6,6 =6,6
| 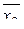 =9,0 =9,0
| 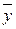 =29,4 =29,4
| – | – | 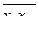 =68,8 =68,8
| 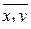 =207,8 =207,8
| 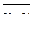 =288,0 =288,0
| – |
Решение. Составим систему нормальных уравнений МНК:
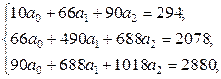
Выразим из 1-го уравнения системы a0 = 29,4 – 6,6·a1 – 9·a2.
Подставив во 2-е уравнение это выражение, получим:
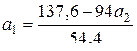 .
.
Далее подставляем в 3-е уравнение вместо a0 и a1 полученные выражения и решаем его относительно a2 с точностью не менее 3-х знаков после запятой. Итак:
a0 = 12,508; a1 = 2,672; a2 = – 0,082; 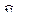 = 12,508 + 2,672·х1 – 0,082·х2.
= 12,508 + 2,672·х1 – 0,082·х2.
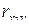 =
= 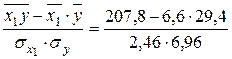 = 0,884;
= 0,884;
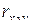 =
= 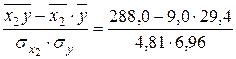 = 0,777;
= 0,777;
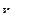 =
= 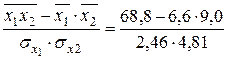 = 0,893;
= 0,893;
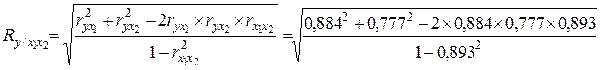 =0,893.
=0,893.
Проверим значимость r (α = 0,01 и ν = 7):
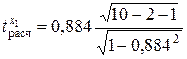 = 5,00;
= 5,00; 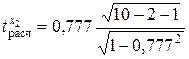 = 3,27.
= 3,27.
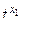 =5,00 > tтабл=3,50 – коэффициент корреляции x1 значим;
=5,00 > tтабл=3,50 – коэффициент корреляции x1 значим;
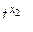 =3,27 < tтабл=3,50 – коэффициент корреляции x2 не значим.
=3,27 < tтабл=3,50 – коэффициент корреляции x2 не значим.
Произведенные расчеты подтверждают условие включения факторных признаков в регрессионную модель – между результативным и факторными признаками существует тесная связь ( 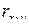 = 0,884;
= 0,884; 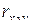 = 0,777), однако между факторными признаками достаточно существенная связь (
= 0,777), однако между факторными признаками достаточно существенная связь ( 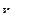 = 0,893). Включение в модель фактора x2 незначительно увеличивает коэффициент корреляции (
= 0,893). Включение в модель фактора x2 незначительно увеличивает коэффициент корреляции ( 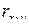 = 0,884;
= 0,884; 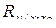 =0,893), поэтому включение в модель фактора x2 нецелесообразно.
=0,893), поэтому включение в модель фактора x2 нецелесообразно.
Вычислим стандартизованные коэффициенты уравнения множественной регрессии:
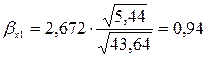
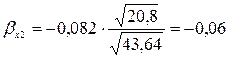
Отсюда вычислим частные коэффициенты детерминации:
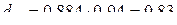
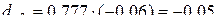
т.е. вариация результативного признака объясняется главным образом вариацией фактора x1.
Вычислим частные коэффициенты эластичности:
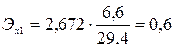
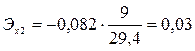
Проверим адекватность модели на основе критерия Фишера:
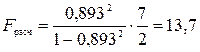
Найдем значение табличного значения F-критерия для уровня значимости α=0,05 и числе степеней свободы ν1 = 2, ν2 = 10 –2 – 1 : Fтабл=4,74. Превышение значения Fрасч над значением Fтабл позволяет считать коэффициент множественной детерминации значимым, а соответственно и модель – адекватной, а выбор формы связи - правильным.
Тема: Показатель корреляции рангов
ЗАДАЧА 89
Изучается товарооборот и суммы издержек обращения по ряду магазинов. Рассчитать показатель корреляции рангов между товарооборотом и издержками обращения по следующим данным:
| № магазина | Товарооборот | Издержки обращения |
| 1 | 480 | 30 |
| 2 | 510 | 25 |
| 3 | 530 | 31 |
| 4 | 540 | 28 |
| 5 | 570 | 29 |
| 6 | 590 | 32 |
| 7 | 620 | 36 |
| 8 | 640 | 36 |
| 9 | 650 | 37 |
| 10 | 660 | 38 |
Из таблицы видно, что с ростом товарооборота растут и издержки обращения.
Для расчета показателя корреляции рангов от величин абсолютных перейдем к рангам по такому правилу: самое меньшее значение ранг 1, затем ранг 2 и т.д. Если встречаются одинаковые значения, то каждый из них заменяется средним. Следует помнить, что перед заменой абсолютных значений рангами, всегда один из столбцов показателей необходимо отсортировать по возрастанию не нарушив связь между парами соседних показателей ( в данном примере пара: товарооборот - издержки) В результате получим следующую таблицу:
| Товарооборот | Издержки обращения |
|
|
| 1 | 4 | -3 | 9 |
| 2 | 1 | 1 | 1 |
| 3 | 5 | -2 | 4 |
| 4 | 2 | 2 | 4 |
| 5 | 3 | 2 | 4 |
| 6 | 6 | 0 | 0 |
| 7 | 7,5 | -0,5 | 0,25 |
| 8 | 7,5 | 0,5 | 0,25 |
| 9 | 9 | 0 | 0 |
| 10 | 10 | 0 | 0 |
Таким образом, столбцы «Товарооборот» и «Издержки обращения» отражают ранги, а не абсолютные величины. При этом равные значения издержек – 36 и 36 рассчитывается как средняя величина рангов (7+8)/2=7,5. Величина 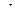 =«Товарооборот» - «Издержки обращения»=1-4= - 3
=«Товарооборот» - «Издержки обращения»=1-4= - 3
Тогда, из таблицы по формуле 5.26 рассчитаем показатель корреляции рангов:
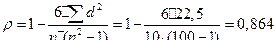
Полученный показатель свидетельствует о достаточно тесной связи между товарооборотом и издержками.
Сравним показатель корреляции рангов с коэффициентом корреляции (формула 5.17):
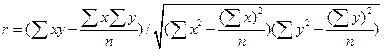
Для этого рассчитаем вспомогательную таблицу:
| № магазина | Товарооборот
| Издержки обращения

|
|
|
|
| 1 | 480 | 30 | 230400 | 900 | 14400 |
| 2 | 510 | 25 | 260100 | 625 | 12750 |
| 3 | 530 | 31 | 280900 | 961 | 16430 |
| 4 | 540 | 28 | 291600 | 784 | 15120 |
| 5 | 570 | 29 | 324900 | 841 | 16530 |
| 6 | 590 | 32 | 348100 | 1024 | 18880 |
| 7 | 620 | 36 | 384400 | 1296 | 22320 |
| 8 | 640 | 36 | 409600 | 1296 | 23040 |
| 9 | 650 | 37 | 422500 | 1369 | 24050 |
| 10 | 660 | 38 | 435600 | 1444 | 25080 |
Итого
5790
322
3388100
10540
188600
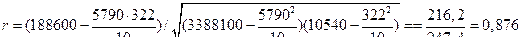
Таким образом, мы видим, что показатели 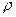 и
и 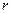 близки между собой, хотя теоретически коэффициент корреляции более точен.
близки между собой, хотя теоретически коэффициент корреляции более точен.
5.3 Контрольные задачи
Тема: расчет коэффициентов парной корреляции
ЗАДАЧА 90
Туристическая компания предлагает места в гостиницах приморского курорта. Менеджера компании интересует, насколько возрастает привлекательность компании в зависимости от её расстояния до пляжа. С этой целью по 14 гостиницам города была выяснена среднегодовая наполняемость номеров и расстояние в км. до пляжа.
| Расстояние | 0,1 | 0,1 | 0,2 | 0,3 | 0,4 | 0,4 | 0,5 | 0,6 | 0,7 | 0,7 | 0,8 | 0,8 | 0,9 | 0,9 |
| Наполняемость, % | 92 | 95 | 96 | 90 | 89 | 86 | 90 | 83 | 85 | 80 | 78 | 76 | 72 | 75 |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.
ЗАДАЧА 91
Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей (Х) и стоимостью ежемесячного тех. обслуживания (Y). Для выяснения характера этой связи было отобрано 15 автомобилей.
| Х | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Y | 13 | 16 | 15 | 20 | 19 | 21 | 26 | 24 | 30 | 32 | 30 | 35 | 34 | 40 | 39 |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.
ЗАДАЧА 92
Врач исследователь выясняет зависимость площади поражённой части лёгких у людей, заболевших эмфиземой лёгких, от числа лет курения. Статистические данные, собранные им в некоторой области имеют следующий вид:
| Число лет курения | 25 | 36 | 22 | 15 | 48 | 39 | 42 | 31 | 28 | 33 |
| Площадь поражённой части лёгкого, % | 55 | 60 | 50 | 30 | 75 | 70 | 70 | 55 | 30 | 35 |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов. Если человек курил 30 лет, то сделайте прогноз о степени поражения лёгких у случайно выбранного пациента
ЗАДАЧА 93
Компания, занимающаяся продажей радиоаппаратуры, установила на DVD проигрыватель определённой модели цену, диффириенцированную по регионам. Следующие данные показывают цену в 8 различных регионах и соответствующее им число продаж.
| Число продаж, шт. | 420 | 380 | 350 | 400 | 440 | 380 | 450 | 420 |
| Цена, тыс. руб. | 5,5 | 6 | 6,5 | 6 | 5 | 6,5 | 4,5 | 5 |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,01. Постройте уравнение регрессии и объясните смысл полученных результатов.
ЗАДАЧА 94
Опрос 10 студентов Академии народного хозяйства позволяет выявить зависимость между средним баллом по результатам предыдущей сессии и числом часов в неделю затраченных студентом на самостоятельную подготовку.
| Средний балл | 4,6 | 4,3 | 3,8 | 3,8 | 4,2 | 4,3 | 3,8 | 4 | 3,1 | 3,9 |
| Число часов | 25 | 22 | 9 | 15 | 15 | 30 | 20 | 30 | 10 | 17 |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов. Если студент занимается самостоятельно по 12 часов в неделю, то каков прогноз успеваемости?
ЗАДАЧА 95
Перед сдачей экзаменов в конце семестра в 20 группах студентов Академии народного хозяйства был проведён опрос о том, какую оценку по сдаваемым в сессию курсам они ожидают получить. После сессии средние полученные оценки были сопоставлены со средними ожидаемыми.
Результаты приведены в таблице:
| Ожидаемая | 3,4 | 3,1 | 3 | 2,8 | 3,7 | 3,5 | 2,9 | 3,7 | 3,5 | 3,2 |
| Полученная | 4,1 | 3,4 | 3,3 | 3 | 4,7 | 4,6 | 3 | 4,6 | 4,6 | 3,6 |
| Ожидаемая | 3 | 3,5 | 3,3 | 3,1 | 3,3 | 3,9 | 2,9 | 3,2 | 3,4 | 3,4 |
| Полученная | 3,5 | 4 | 3,6 | 3,1 | 3,3 | 4,5 | 2,8 | 3,7 | 3,8 | 3,9 |
Рассчитайте линейный коэффициент корреляции Пирсона, оцените его значимость при α = 0,05.
ЗАДАЧА 96
Имеется случайная выборка из 10 семей для изучения связи между числом телевизоров (Y) в домохозяйстве и числом членов семьи (Х)
| Х | 6 | 2 | 4 | 3 | 4 | 4 | 6 | 3 | 2 | 2 |
| Y | 4 | 1 | 3 | 2 | 2 | 3 | 4 | 1 | 2 | 2 |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,01. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.
ЗАДАЧА 97
Имеются данные о стаже работы (Х, лет) и выработке одного рабочего за смену (Y, шт.)
| Х | 1 | 3 | 4 | 5 | 6 | 7 |
| Y | 14 | 15 | 18 | 20 | 22 | 25 |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.
ЗАДАЧА 98
Имеются выборочные данные о глубине вспашки полей под озимые культуры (Х, см.) и их урожайность (Y, га)
| Х | 10 | 15 | 20 | 25 | 30 |
| Y | 5 | 10 | 16 | 20 | 24 |
При α = 0,05 установить значимость статистической связи между признаками Х и Y. Если признаки коррелируют, постройте уравнение регрессии и объясните его смысл. Сделайте прогноз урожайности пшеницы при глубине вспашки 22 см.
ЗАДАЧА 99
Из студентов 3-го курса групп ЭВМ отобраны случайным образом 10 человек и подсчитаны средние оценки, полученные ими на 1-ом (Х) и 3-м (Y) курсе.
| Х | 3,5 | 4 | 3,8 | 4,6 | 3,9 | 3 | 3,5 | 3,9 | 4,5 | 4,1 |
| Y | 4,2 | 3,9 | 3,8 | 4,5 | 4,2 | 3,4 | 3,8 | 3,9 | 4,6 | 3 |
Полагая, что между Х и Y имеет место линейная зависимость, определите выборочное уравнение линейной регрессии и объясните смысл полученных коэффициентов. Каковы значимость коэффициента корреляции, направление и теснота связи между показателями Х и Y, если α = 0,05?
ЗАДАЧА 100
Определите тесноту связи между возрастом самолёта (Х, лет) и стоимостью его эксплуатации (Y, млн. руб.) по следующим данным:
| Х | 1 | 2 | 3 | 4 | 5 |
| Y | 2 | 4 | 5 | 8 | 10 |
Установите значимость коэффициента корреляции. Если он значим, то постройте уравнение регрессии и объясните его смысл. Каким будет прогноз стоимости эксплуатации самолёта, если его возраст 1,5 года, а уровень значимости принять равным 0,05?
Тема: расчет множественной корреляции
ЗАДАЧА 101
Считая зависимость между показателями Yи 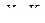 линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели.
линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели.
|
| 20 | 21,5 | 23 | 24 | 25,5 | 27 | 28,1 | 28 | 29,5 | 33 |
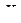
| 7 | 7,5 | 8 | 8,5 | 9 | 9,5 | 10 | 10,5 | 11 | 11,5 |
| Y | 0,04 | 0,08 | 0,12 | 0,04 | 0,12 | 0,2 | 0,12 | 0,08 | 0,08 | 0,1 |
ЗАДАЧА 102
Считая зависимость между показателями Yи 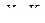 линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели
линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели
| | 30,4 | 31,0 | 31,0 | 31,2 | 31,7 | 31,7 | 31,9 | 32,1 | 31,0 | 32,0 |
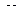
| 4 | 3 | 7 | 6 | 5 | 2 | 3 | 8 | 9 | 2 |
| Y | 13,8 | 14 | 14,1 | 14,2 | 14,3 | 14,4 | 14,5 | 14,6 | 13,9 | 14,7 |
ЗАДАЧА 103
Считая зависимость между показателями Yи 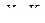 линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели
линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели
| | 4,4 | 4,2 | 3,6 | 3,6 | 3,7 | 6,3 | 5,0 | 5,6 | 4,8 | 5,0 |
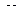
| 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4 |
| Y | 1,75 | 1,62 | 1,43 | 1,52 | 1,49 | 2,512 | 2 | 2,31 | 1,9 | 2 |
ЗАДАЧА 104
Считая зависимость между показателями Yи 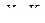 линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели
линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели
| | 3,4 | 3,2 | 2,6 | 2,7 | 1,7 | 0,7 | 1,0 | 1,8 | 1,7 | 0,9 |
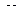
| 1,9 | 2,5 | 2,4 | 2,2 | 1,8 | 3,8 | 3,9 | 3 | 3,5 | 3,7 |
| Y | 2 | 2 | 1,5 | 1,5 | 1 | 0,4 | 0,6 | 1 | 1 | 0,5 |
Тема: Показатель корреляции рангов
ЗАДАЧА 105
Изучается зависимость выпуска продукции от численности персонала по ряду предприятий области. Рассчитать показатель корреляции рангов и коэффициент корреляции по следующим данным:
| № предприятия | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Численность персонала (чел.) х | 400 | 150 | 320 | 210 | 540 | 270 | 390 | 80 | 530 | 320 | 240 | 580 | 410 | 260 | 190 | 500 | 680 | 400 | 360 | 550 |
| Выпуск продукции (млн.руб.) у | 95 | 22 | 51 | 54 | 110 | 58 | 80 | 15 | 110 | 73 | 50 | 140 | 90 | 64 | 40 | 86 | 168 | 85 | 80 | 130 |
ЗАДАЧА 106
Рассчитать показатель корреляции рангов и коэффициент корреляции по следующим данным и сделать выводы:
| Х | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 | 1,1 | 1,2 | 1,3 | 1,4 |
| Y | 1,3 | 1,21 | 1,12 | 1,62 | 1,73 | 1,45 | 1,44 | 1,52 | 1,68 | 1,7 |
ЗАДАЧА 107
Рассчитать показатель корреляции рангов и коэффициент корреляции по следующим данным и сделать выводы:
| Х | 178 | 170 | 181 | 173 | 169 | 178 | 177 | 165 | 187 | 182 |
| Y | 72 | 65 | 92 | 75 | 68 | 79 | 78 | 67 | 80 | 81 |
ЗАДАЧА 108
Рассчитать показатель корреляции рангов и коэффициент корреляции по следующим данным и сделать выводы:
| Х | 159 | 182 | 178 | 173 | 176 | 173 | 198 | 187 | 191 | 170 |
| Y | 56 | 82 | 77 | 63 | 80 | 65 | 85 | 89 | 87 | 72 |
ЗАДАЧА 109
Рассчитать показатель корреляции рангов и коэффициент корреляции по следующим данным и сделать выводы:
| Х | 19 | 25 | 24 | 22 | 18 | 38 | 39 | 30 | 35 | 38 |
| Y | 20 | 20 | 15 | 15 | 10 | 4 | 6 | 10 | 10 | 5 |
ЗАДАЧА 110
Рассчитать показатель корреляции рангов и коэффициент корреляции по следующим данным и сделать выводы:
| Х | 6,2 | 6,8 | 7 | 7,3 | 7,5 | 8,2 | 8,4 | 8,7 | 8,8 | 9 |
| Y | 17,1 | 16 | 15,1 | 15 | 14,1 | 13,3 | 13,1 | 12,5 | 12 | 11,9 |
ЗАДАЧА 111
Рассчитать показатель корреляции рангов и коэффициент корреляции по следующим данным и сделать выводы:
| Х | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 | 45 |
| Y | 1,34 | 1,85 | 3,41 | 3,85 | 4,45 | 4,98 | 5,63 | 5,74 | 6,82 | 7 |
6. Ряды динамики
6.1 Методические указания
Анализ динамических рядов
Динамический ряд представляет собой хронологическую последовательность числовых значений статистических показателей.
Виды рядов динамики (РД):
1) моментные (моментальные) РД;
2) интервальные РД;
3) РД с нарастающими итогами;
4) производные РД.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Пример моментного ряда динамики:
| Дата | 1.01.2007 | 1.04.2008 | 1.07.2009 | 1.10.2010 | 1.01.2011 |
| Число работников, чел. | 192 | 190 | 195 | 198 | 200 |
Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени. Каждый уровень интервального ряда складывается из данных за более короткие интервалы. Пример интервального ряда динамики:
| Год | 2006 | 2007 | 2008 | 2009 | 2010 |
| Объем розничного товарооборота, тыс. руб. | 885,7 | 932,6 | 980,1 | 1028,7 | 1088,4 |
Статистическое отображение развития изучаемого явления во времени может быть представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями в результатах развития изучаемых показателей не только за данный отчетный период, но и с учетом предшествующих периодов. При составлении таких рядов производится последовательное суммирование смежных уровней. Этим достигается суммарное обобщение результата развития изучаемого показателя с начала отчетного периода (месяца, квартала, года и т.д.).
Производные ряды – ряды, уровни которых представляют собой не непосредственно наблюдаемые значения, а производные величины: средние или относительные.
Основные направления изучения закономерностей развития социально-экономических явлений с помощью рядов динамики:
- характеристика уровней развития изучаемых явлений во времени;
- измерение динамики изучаемых явлений посредством системы статистических показателей;
- выявление и количественная оценка основной тенденции развития (тренда);
- изучение периодических колебаний;
- экстраполяция и прогнозирование.
Таблица 6.1 Уровни (показатели) ряда динамики
| Показатель | Формула | |
| Базисные | Абсолютный прирост | Δ 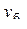 = yi – у0 (6.1) = yi – у0 (6.1)
|
| Темп роста | 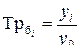 (6.2) (6.2)
| |
| Темп прироста | 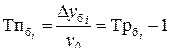 (6.3) (6.3)
| |
| Цепные | Абсолютный прирост | Δ  = yi – yi-1 (6.4) = yi – yi-1 (6.4)
|
| Темп роста | 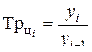 (6.5) (6.5)
| |
| Темп прироста |
| |
| Темп наращивания |
| |
| Абсолютное значение 1% прироста |
| |
| Средние | Абсолютный прирост |
|
| Темп роста |
| |
| Темп прироста |
|
Средний уровень ряда динамики характеризует типическую величину абсолютных уровней.
Средний уровень интервального ряда определяется по формуле средней арифметической простой:
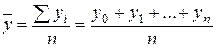 , (6.12)
, (6.12)
где n – число уровней.
В моментном ряду динамики с равностоящими датами средний уровень определяется по формуле средней хронологической простой:
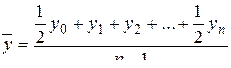 . (6.13)
. (6.13)
В моментном ряду динамики с неравноотстоящими датами средний уровень определяется по формуле средней хронологической взвешенной:
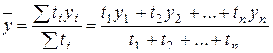 , (6.14)
, (6.14)
где у i – уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени ti.
Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
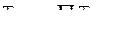 ;
; 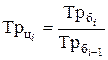 . (6.15)
. (6.15)
Методы анализа тенденций рядов динамики
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер.
Основная тенденция (тренд) – изменение, определяющее общее направление развития, это систематическая составляющая долговременного действия.
Задача – выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. Методы выявления тренда:
1) Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Средняя, исчисленная по укрупненным интервалам, позволяет выявить направление и характер (ускорение или замедление роста) основной тенденции развития, в то время как слишком малые интервалы между наблюдениями приводят к появлению ненужных деталей в динамике процесса, засоряющих общую тенденцию.
| Месяц | Объем выпуска, млн.руб. | Месяц | Объем выпуска, млн.руб. |
| Январь | 5,1 | Июль | 5,6 |
| Февраль | 5,4 | Август | 5,9 |
| Март | 5,2 | Сентябрь | 6,1 |
| Апрель | 5,3 | Октябрь | 6,0 |
| Май | 5,6 | Ноябрь | 5,9 |
| Июнь | 5,8 | Декабрь | 6,2 |
Различные направления изменений уровней ряда по отдельным месяцам затрудняют выводы об основной тенденции производства. Если соответствующие месячные уровни объединить в квартальные и вычислить среднемесячный выпуск продукции по кварталам, т.е. укрупнить интервалы, то решение задачи упрощается.
| Квартал | Объем производства, млн.руб. | |
| в квартал | в среднем в месяц | |
| 1 | 15,7 | 5,23 |
| 2 | 16,7 | 5,57 |
| 3 | 17,6 | 5,87 |
| 4 | 18,1 | 6,03 |
После укрупнения интервалов основная тенденция роста производства стала очевидной: 5,23<5,57<5,87<6,03 млн.руб.
2) Метод скользящей средней заключается в том, что исчисляется средней уровень из определенного числа (обычно нечетного) первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная с третьего и т.д. Таким образом, средняя как бы “скользит” по ряду динамики, передвигаясь на один срок.
Недостатком сглаживания ряда является укорачивание сглаженного ряда по сравнению с фактическим, а, следовательно, потеря информации.
| Год | Урожайность, ц/га | Скользящая средняя | |
| трехлетняя | пятилетняя | ||
| 1991 | 15,4 | – | – |
| 1992 | 14,0 | 15,7 = 15,4+14,0+ +17,6)/3 | – |
| 1993 | 17,6 | 15,7 = 14,0+17,6+ +15,4)/3 | 14,7 |
| 1994 | 15,4 | 14,6 | 15,1 |
| 1995 | 10,9 | 14,6 | 15,3 |
| 1996 | 17,5 | 14,5 | 15,5 |
| 1997 | 15,0 | 17,0 | 15,2 |
| 1998 | 18,5 | 15,9 | 16,0 |
| 1999 | 14,2 | 15,9 | – |
| 2000 | 14,9 | – | – |
| Итого | 153,4 | ||
Сглаженный ряд урожайности по трехлетиям короче фактического на один член ряда в начале и в конце, по пятилетиям – на два члена в начале и в конце ряда. Он меньше, чем фактический, подвержен колебаниям из-за случайных причин, и четче выражает основную тенденцию роста урожайности за изучаемый период, связанную с действием долговременно существующих причин и условий развития.
Укрупнение интервалов и метод скользящей средней дают возможность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных или волнообразных колебаний. Получить обобщенную статистическую модель тренда посредством этих методов нельзя.
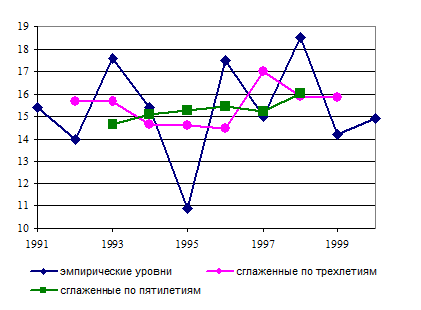
Рис. 6.1. Эмпирические и сглаженные уровни ряда динамики
3) Аналитическое выравнивание ряда динамики используется для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней ряда динамики во времени.
Общая тенденция развития рассчитывается как функция времени:
ŷ t = f(t), (6.16)
где ŷ t – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Определение теоретических (расчетных) уровней ŷ t производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики.
Простейшими моделями, выражающими тенденцию развития, являются (где a0, a1 – параметры уравнения; t – время):
Линейная функция (прямая) ŷ t = a0 + a1·t. (6.17)
Показательная функция 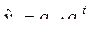 . (6.18)
. (6.18)
Степенная функция (парабола) ŷ t = a0 + a1·t + a2·t2. (6.19)
Расчет параметров функции обычно производится методом наименьших квадратов..
Выравнивание ряда динамики по прямой ŷ t = a0 + a1·t. Параметры a0, a1 согласно МНК находятся решением следующей системы нормальных уравнений:
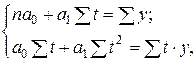 (6.20)
(6.20)
где y – фактические (эмпирические) уровни ряда;
t – время (порядковый номер периода или момента времени).
S t = 0, так что система нормальных уравнений (6.20) принимает вид:
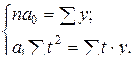 (6.21)
(6.21)
Отсюда можно выразить коэффициенты регрессии:
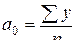 ; (6.22)
; (6.22)
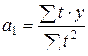 . (6.23)
. (6.23)
Если расчеты выполнены правильно, то S y = S ŷ.
Сезонные колебания
Уровни ряда динамики формируются под влиянием различных взаимодействующих факторов, одни из которых определяют тенденцию развития, а другие –колебания (вариацию)
Колебания уровней ряда носят различный характер. Наряду с трендом выделяют циклические (долгопериодические), сезонные (обнаруживаемые в рядах, где данные приведены за кварталы или месяцы) и случайные колебания.

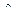 – линия тренда
– линия тренда
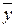 – средний уровень
– средний уровень
у i – фактические уровни
Рис. 6.2. Виды колебаний рядов динамики
Периодические колебания являются результатом влияния природно-климатических условий, общих экономических факторов, а также многочисленных и разнообразных факторов, которые часто являются регулируемыми.
В широком понимании к сезонным относят все явления, которые обнаруживают в своем развитии четко выраженную закономерность периодических изменений, т.е. более или менее устойчиво повторяющиеся колебания уровней.
Динамический ряд в этом случае называют сезонным рядом динамики.
Метод изучения и измерения сезонности заключается в построении специальных показателей, которые называются индексами сезонности.
Индексами сезонности являются процентные отношения фактических внутригрупповых уровней к теоретическим уровням, выступающим в качестве базы сравнения. Порядок определения индекс сезонности:
1) Для каждого месяца рассчитывается средняя величина уровня
2) Затем вычисляется среднемесячный уровень для всего ряда
3) Определяется показатель сезонной волны – индекс сезонности Is:
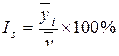 , (6.24)
, (6.24)
где 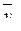 – средний уровень для каждого месяца;
– средний уровень для каждого месяца;
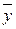 – среднемесячный уровень для всего ряда.
– среднемесячный уровень для всего ряда.
Когда уровень проявляет тенденцию к росту или к снижению, то отклонения от постоянного среднего уровня могут исказить сезонные колебания.
Статистические методы прогнозирования экономических показателей
Прогнозирование – процесс определения возможных в будущем значений экономических показателей на основании уже известных.
Различают прогнозы по периоду упреждения: оперативные (до 1 мес.); краткосрочные (до 1 года); среднесрочные (1 – 5 лет); долгосрочные (более 5 лет).
Различают методы прогнозирования:
Экстраполяция тенденций:
- упрощенные приемы, основанные на средних показателях динамики (средние темпы роста, прироста);
- аналитические методы (метод наименьших квадратов, тренды, т.е. математические функции);
- адаптивные методы, учитывающие степень устаревания данных (методы скользящих и экспоненциальных средних, методы авторегрессии).
Методы статистического моделирования:
- статические (методы парной и множественной регрессии);
- динамические (анализ динамических рядов):
- методы агрегатного моделирования (разложение ряда на тенденции, сезонность, случайные составляющие);
- методы регрессии по взаимосвязанным рядам динамики (включаются в модель не только факторы, но и лаговые переменные);
- методы регрессии по пространственно-временной информации (для каждого ряда строится регрессионная модель по совокупности объектов).
Прогнозирование на основе экстраполяции тренда
Тренд – основная тенденция развития. Методы выявления тренда называются методами выравнивания временного ряда (метод наименьших квадратов, скользящей средней, конечных разностей).
При наличии тенденции в ряду динамики модель уровня динамического ряда:
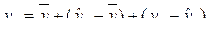 , (6.25)
, (6.25)
где 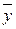 – средний уровень динамического ряда;
– средний уровень динамического ряда;
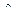 – теоретический (расчетный, трендовый) уровень;
– теоретический (расчетный, трендовый) уровень;
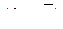 – эффект тенденции;
– эффект тенденции;
 – случайная составляющая (остаточные колебания) ε.
– случайная составляющая (остаточные колебания) ε.
Чем меньше остаточные колебания  , тем выше адекватность (практическая значимость) модели. Следовательно, результаты прогноза зависят от типа кривой тренда ŷ(t).
, тем выше адекватность (практическая значимость) модели. Следовательно, результаты прогноза зависят от типа кривой тренда ŷ(t).
Кривые тренда традиционно делятся на
1. Линейный тренд ŷ t = a0 + a1·t
2. Параболический тренд ŷ t = a0 + a1·t + a2·t2
3. Показательная кривая 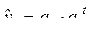 ,
, 
4. Логистическая кривая 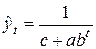 (кривая Перла-Рида) (кривые Гомперца)
(кривая Перла-Рида) (кривые Гомперца)
Выбор наилучшего тренда при прогнозировании
При выборе уравнения тренда можно руководствоваться средней ошибкой аппроксимации
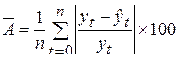 , %. (6.26)
, %. (6.26)
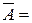 5÷7% – хорошая аппроксимация.
5÷7% – хорошая аппроксимация.
Доверительные интервалы прогноза определяются по дисперсии уточненного тренда
 , %. (6.27)
, %. (6.27)
где yt – фактические уровни ряда;
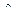 – расчетные (трендовые) значения;
– расчетные (трендовые) значения;
n – длина ряда;
m – число параметров в уравнении тренда (без свободного члена).
Доверительный интервал с учетом табличного значения критерия Стьюдента 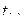 , равен
, равен
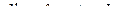 . (6.28)
. (6.28)
6.2 Пример решения задач
Тема: приведение рядов динамики к сопоставимому виду
ЗАДАЧА 112
В 2007 произошло административное изменение границ одного из субьектов РФ.
Имеются следующие данные о валом сборе овощей агрофирмами и фермерскими хозяйствами в тыс.ц в старых и новых границах:
| в границах |
2005
2006
2007
2008
2009
2010
старых
416
432
450
-
-
-
новых
-
-
630
622,5
648,1
684,4
Привести ряды динами к сопоставимому виду.
Решение. Для приведения рядов динамики к сопоставимому виду определим для 2007 года
Коэффициент соотношения уровней двух рядов: 630:450 = 1,4. Умножая этот коэффициент на уровни 1-го ряда получаем их сопоставимость с уровнями 2-го ряда:
| в границах |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
| старых | 416 | 432 | 450 | - | - | - |
| новых |
582,4 |
604,8 | 630 | 622,5 | 648,1 | 684,4 |
Тема: Определение среднего уровня ряда динамики
ЗАДАЧА 113
На 1 января 2011 года остаток вклада составлял 50000 рублей. В течении 1 квартала имели место следующие изменения величины остатков вклада (руб.):
| Дата изменения размера вклада, руб. | ||||||
| 05.01 | 17.01 | 02.02 | 21.02 | 13.03 | 20.03 | 28.03 |
| +15000 | -20000 | - | +50000 | - | - | +10000 |
Определить среднеквартальный размер вклада
Решение. Для определения среднего уровня моментного ряда используется формула 6.14:
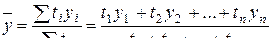
Рассчитаем размер вклада за 1 квартал 2011 года:
| Период | Число дней в периоде, 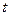
| Размер вклада (руб.) 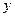
|
|
| 01.01-05.01 | 4 | 50000 | 200000 |
| 05.01-17.01 | 12 | 65000 | 780000 |
| 17.01-21.02 | 35 | 45000 | 1575000 |
| 21.02-28.03 | 35 | 95000 | 3325000 |
| 28.03-01.04 | 4 | 105000 | 420000 |
| Итого | 90 | - | 6300000 |
Тогда 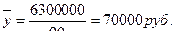
Тема: Расчет показателей ряда динамики
ЗАДАЧА 114
Определить все возможные показатели динамики, включая средние.
| Год | Численность работающих в отрасли, тыс. чел. |
| 2007 | 10,4 |
| 2008 | 10,6 |
| 2009 | 11,0 |
| 2010 | 11,3 |
| 2011 | 11,7 |
Решение. Рассчитаем показатели динамики по формулам 6.1 – 6.7
Результаты решения сведем в таблицу:
| Год | Численность работающих, тыс. чел. | Абсолютный прирост | Темп роста | Темп прироста | Темп наращивания | |||
| базисный | цепной | базисный | цепной | базисный | цепной | |||
| 2007 | 10,4 | - | - | - | - | - | - | - |
| 2008 | 10,6 | 0,2 | 0,2 | 1,02 | 1,02 | 0,02 | 0,02 | 0,02 |
| 2009 | 11 | 0,6 | 0,4 | 1,058 | 1,038 | 0,058 | 0,038 | 0,038 |
| 2010 | 11,3 | 0,9 | 0,3 | 1,087 | 1,027 | 0,087 | 0,027 | 0,029 |
| 2011 | 11,7 | 1,3 | 0,4 | 1,125 | 1,035 | 0,125 | 0,035 | 0,038 |
Абсолютный прирост базисный: Абсолютный прирост цепной:
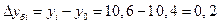

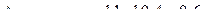

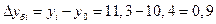

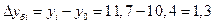

Темп роста базисный: Темп роста цепной:
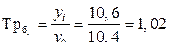
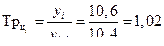
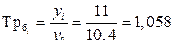
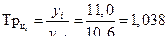
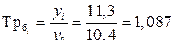
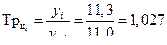
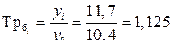
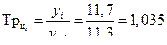
Темп прироста базисный: Темп прироста цепной:
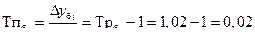
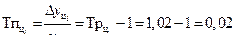
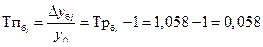
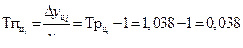

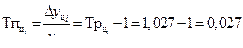
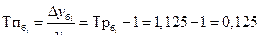
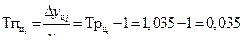
Темп наращивания:
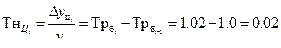
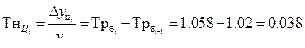
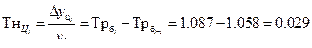
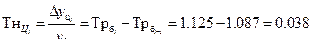
Средний уровень ряда (моментный ряд с равностоящими датами) 6.13
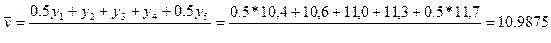
Средний абсолютный прирост 6.9
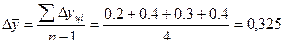
Средний темп роста 6.10
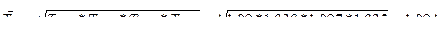
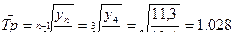
Средний темп прироста 6.11
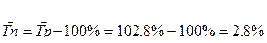
ЗАДАЧА 115
Рассчитать недостающие показатели динамики
| Год | Пассажирооборот (млр.пасс-км.) | Цепные показатели динамики | |||
| Абсолютный прирост | Темп роста | Темп прироста % | Абсолютное значение 1% прироста (млрд.пасс.км) | ||
| 2006 | 127,0 | - | - | - | - |
| 2007 |
|
| 1,102 |
|
|
| 2008 |
|
|
| 7,1 |
|
| 2009 | 164,6 |
|
|
|
|
| 2010 |
|
|
|
|
|
| 2011 |
|
|
| 9,9 | 1,75 |
Решение. Решение задачи целесообразно начать с определения отсутствующих в таблице уровней ряда динамики (столбец «Пассажирооборт»).
1. Уровень 2007 года можно найти используя уровень 2006 года и показатель темп роста для 2006 года:
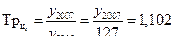 откуда
откуда 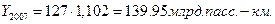
2. Уровень 2008 года определяется так:
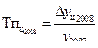 откуда
откуда 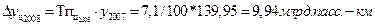
тогда
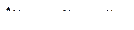 и
и 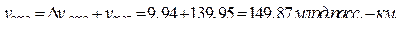
3. Уровень 2010 года определяется по показателям 2011 года так:
 откуда
откуда 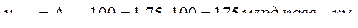
4. Уровень 2011 года определяется по показателям 2011 года (темпу прироста) так:
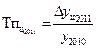 откуда
откуда 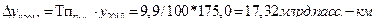
тогда
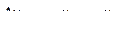 и
и 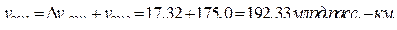
| Год | Пассажирооборот (млр.пасс-км.) | |
| 2006 | 127,0 | |
| 2007 | 139,95 | |
| 2008 | 149,87 | |
| 2009 | 164,6 | |
| 2010 | 175 | |
| 2011 | 192,33 |
Имея все уровни ряда динамики нетрудно рассчитать недостающие показатели:
| Год | Пассажирооборот (млр.пасс-км.) | Цепные показатели динамики | |||
| Абсолютный прирост | Темп роста | Темп прироста % | Абсолютное значение 1% прироста (млрд.пасс.км) | ||
| 2006 | 127,0 | - | - | - | - |
| 2007 | 139,95 | 12,95 | 1,102 | 10,2 | 1,270 |
| 2008 | 149,87 | 9,92 | 1,071 | 7,1 | 1,399 |
| 2009 | 164,6 | 14,73 | 1,098 | 9,8 | 1,498 |
| 2010 | 175 | 10,4 | 1,064 | 6,4 | 1,646 |
| 2011 | 192,33 | 17,3 | 1,099 | 9,9 | 1,750 |
Тема: Метод аналитического выравнивания и прогнозирования
ЗАДАЧА 116
Рассчитать интервальный прогноз урожайности на 2011 год, используя линейную трендовую модель по следующим данным урожайности зерновых культур, для вероятности Р=0,95:
| Год | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| y | 15,4 | 14 | 17,6 | 15,4 | 10,9 | 17,5 | 15 | 18,5 | 14,2 | 14,9 |
Для выравнивания ряда используем линейную трендовую модель – уравнение прямой
ŷ t = a0 + a1·t. n = 10.. При этом заменим абсолютные показатели времени на относительные так, чтобы 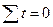 . Расчет уравнения регрессии выполним в табличной форме
. Расчет уравнения регрессии выполним в табличной форме
Таким образом,
S y =153,4; S y · t = 6,8; S t2 = 330.
Вычислим параметры a0, a1 по формулам (6.22, 6.23):
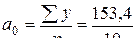 = 15,34;
= 15,34; 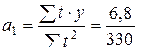 = 0,021.
= 0,021.
Расчет уравнения регрессии
| Год | y | t | t2 | y·t | ŷt | yi – ŷt | (yi – ŷ t)2 |
| 2001 | 15,4 | -9 | 81 | -138,6 | 15,15 | 0,25 | 0,0625 |
| 2002 | 14,0 | -7 | 49 | -98,0 | 15,19 | -1,19 | 1,4161 |
| 2003 | 17,6 | -5 | 25 | -88,0 | 15,23 | 2,37 | 5,6169 |
| 2004 | 15,4 | -3 | 9 | -46,2 | 15,28 | 0,12 | 0,0144 |
| 2005 | 10,9 | -1 | 1 | -10,9 | 15,32 | -4,42 | 19,5364 |
| 2006 | 17,5 | 1 | 1 | 17,5 | 15,36 | 2,14 | 4,5796 |
| 2007 | 15,0 | 3 | 9 | 45,0 | 15,40 | -0,40 | 0,0160 |
| 2008 | 18,5 | 5 | 25 | 92,5 | 15,45 | 3,05 | 9,3025 |
| 2009 | 14,2 | 7 | 49 | 99,4 | 15,49 | -1,29 | 1,6641 |
| 2010 | 14,9 | 9 | 81 | 134,1 | 15,53 | -0,63 | 0,3969 |
| Итого | 153,4 | 0 | 330 | 6,8 | 153,4 | 0 | 42,6050 |
Уравнение прямой будет иметь вид: ŷt = 15,34+0,021·t.
Подставляя в данное уравнение последовательно значения t, находим выравненные уровни ŷt . Проверим расчеты: S y = S ŷt = 153,4.
Следовательно, значения уровней выравненного ряда найдены верно.
Полученное уравнение показывает, что, несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения урожайности: с 2001 по 2010 г. урожайность зерновых культур в среднем возрастала на 0,021 ц/га в год.
Тенденция роста урожайности зерновых культур в изучаемом периоде отчетливо проявляется в результате построения выравненной прямой, что видно на построенной диаграмме.
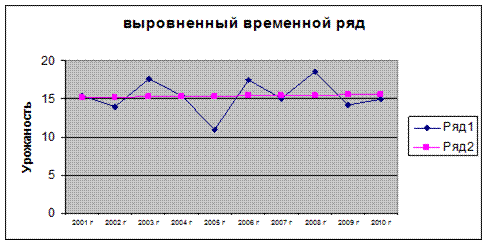
Доверительные интервалы прогноза определяются по дисперсии выровненного тренда, формула 6.26
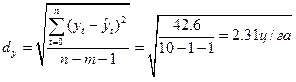
Точечный прогноз на 2011 год:
ŷt = 15,34+0,021·11 =15,57 ц/га
Интервальный прогноз урожайности на 2011 год (формула 6.28) :
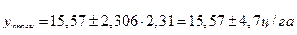
При Р = 0,95 значение t = 2,306
Тема: Расчет индексов сезонности
ЗАДАЧА 117
Рассчитать индексы сезонности по следующим данным:
| Месяц | Объем авиаперевозок | |||
| 2008 | 2009 | 2010 | ||
| 1 | 94,0 | 89,3 | 92,6 | |
| 2 | 98,0 | 93,1 | 96,6 | |
| 3 | 107,6 | 102,2 | 106,2 | |
| 4 | 112,8 | 107,1 | 111,4 | |
| 5 | 121,2 | 115,2 | 119,8 | |
| 6 | 112,0 | 106,4 | 110,6 | |
| 7 | 110,0 | 104,5 | 108,6 | |
| 8 | 102,5 | 97,4 | 101,1 | |
| 9 | 97,0 | 92,2 | 95,6 | |
| 10 | 94,0 | 89,3 | 92,6 | |
| 11 | 96,4 | 91,6 | 95,0 | |
| 12 | 92,5 | 87,9 | 91,1 | |
Решение. Для каждого месяца рассчитывается средняя величина уровня:
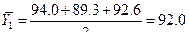
Затем вычисляется среднемесячный уровень для всего ряда
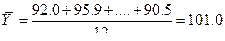
Определяется показатель сезонной волны – индекс сезонности Is:
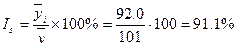
Индексы занесем в таблицу:
| Месяц | Объем пассажирских авиаперевозок | Is, % | |||
| 2008 | 2009 | 2010 | Средний | ||
| 1 | 94,0 | 89,3 | 92,6 | 92,0 | 91,1 |
| 2 | 98,0 | 93,1 | 96,6 | 95,9 | 95,0 |
| 3 | 107,6 | 102,2 | 106,2 | 105,3 | 104,2 |
| 4 | 112,8 | 107,1 | 111,4 | 110,4 | 109,3 |
| 5 | 121,2 | 115,2 | 119,8 | 118,7 | 117,6 |
| 6 | 112,0 | 106,4 | 110,6 | 109,7 | 108,6 |
| 7 | 110,0 | 104,5 | 108,6 | 107,7 | 106,6 |
| 8 | 102,5 | 97,4 | 101,1 | 100,3 | 99,3 |
| 9 | 97,0 | 92,2 | 95,6 | 94,9 | 94,0 |
| 10 | 94,0 | 89,3 | 92,6 | 92,0 | 91,1 |
| 11 | 96,4 | 91,6 | 95,0 | 94,3 | 93,4 |
| 12 | 92,5 | 87,9 | 91,1 | 90,5 | 89,6 |
| Итого | 1237,9 | 1176,0 | 1221,1 | 1211,7 | 1199,7 |
| В среднем | 103,2 | 98,0 | 101,8 | 101,0 | 100,0 |
Средний индекс сезонности для 12 месяцев должен быть равен 100%, тогда сумма индексов должна составлять 1200%. У нас – 1199,7% (погрешность – следствие округлений). Значит, расчеты верны.
Выводы:
1) объем пассажирских авиаперевозок характеризуется ярко выраженной сезонностью;
2) объем пассажирских авиаперевозок по отдельным месяцам года значительно отклоняется от среднемесячного;
3) наибольший объем характерен для мая, наименьший – для декабря.
Для наглядного изображения сезонной волны индексы сезонности изображают в виде графика.
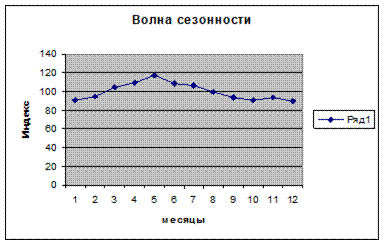
6.3 Контрольные задачи
Тема: приведение рядов динамики к сопоставимому виду
ЗАДАЧА 118
В 2007 произошло административное изменение границ одного из субьектов РФ.
Имеются следующие данные о производстве молока агрофирмами и фермерскими хозяйствами в тыс.т в старых и новых границах:
| в границах |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
| старых | 6,5 | 7,9 | 8,6 | - | - | - |
| новых | - | - | 12,9 | 12,1 | 13,2 | 13,8 |
ЗАДАЧА 119
В 2007 произошло административное изменение границ одного из субьектов РФ.
Имеются следующие данные о производстве мяса агрофирмами и фермерскими хозяйствами в тыс.т в старых и новых границах:
| в границах |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
| старых | 1,9 | 2,1 | 2,4 | - | - | - |
| новых | - | - | 3,3 | 3,4 | 2,8 | 3,8 |
ЗАДАЧА 120
На 1 января 2011 года остаток вклада составлял 70000 рублей. В течении 1 квартала имели место следующие изменения величины остатков вклада (руб.):
| Дата изменения размера вклада, руб. | ||||||
| 05.01 | 17.01 | 02.02 | 21.02 | 13.03 | 20.03 | 28.03 |
| - | - | +30000 | +15000 | -55000 | -20000 | +40000 |
Определить среднеквартальный размер вклада
ЗАДАЧА 121
На 1 января 2011 года остаток вклада составлял 20000 рублей. В течении 1 квартала имели место следующие изменения величины остатков вклада (руб.):
| Дата изменения размера вклада, руб. | ||||||
| 05.01 | 17.01 | 02.02 | 21.02 | 13.03 | 20.03 | 28.03 |
| +15000 | - 10000 | - | +25000 | - | - | +4000 |
Определить среднеквартальный размер вклада
ЗАДАЧА 122
За январь 2011 года произошли следующие изменения в списочном составе работников предприятия, чел.:
Трудилось по списку на 1.01.2011 г - 842
Выбыло с 5.01.2011 г - 4
Зачислено с 12.01.2011 г. - 5
Зачислено с 26.01.2011 г. - 2
Определить среднедневную численность работников за январь месяц
ЗАДАЧА 123
За январь 2011 года произошли следующие изменения в списочном составе работников предприятия, чел.:
Трудилось по списку на 1.01.2011 г - 145
Выбыло с 5.01.2011 г - 3
Зачислено с 12.01.2011 г. - 2
Зачислено с 26.01.2011 г. - 1
Определить среднедневную численность работников за январь месяц
Тема: Расчет показателей ряда динамики
ЗАДАЧА 124
Выпуск продукции предприятием за 2006-2011 гг. характеризуется следующими данными (в сопоставимых ценах в млн.руб)
| 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| 12,3 | 13,4 | 14,8 | 16,4 | 17,8 | 19,9 |
Определить все возможные показатели динамики, включая средние (формулы 6.1-6.11).
ЗАДАЧА 125
Выпуск продукции предприятием за 2006-2011 гг. характеризуется следующими данными (в сопоставимых ценах в млн.руб)
| 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| 23,3 | 24,9 | 26,6 | 27,6 | 29,0 | 32,3 |
Определить все возможные показатели динамики, включая средние (формулы 6.1-6.11).
ЗАДАЧА 126
Выпуск продукции предприятием за 2006-2011 гг. характеризуется следующими данными (в сопоставимых ценах в млн.руб)
| 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| 46,6 | 50,9 | 55,3 | 54,2 | 62,4 | 66,3 |
Определить все возможные показатели динамики, включая средние (формулы 6.1-6.11).
ЗАДАЧА 127
Выпуск продукции предприятием за 2006-2011 гг. характеризуется следующими данными (в сопоставимых ценах в млн.руб)
| 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| 65,3 | 70,8 | 76,3 | 80,0 | 85,0 | 91,0 |
Определить все возможные показатели динамики, включая средние (формулы 6.1-6.11).
ЗАДАЧА 128
Рассчитать недостающие показатели динамики
| Год | Мощность электростанций (млн.Квт) | Цепные показатели динамики | |||
| Абсолютный прирост | Темп роста | Темп прироста | Абсолютное значение 1% прироста (млн.Квт) | ||
| 2005 | 22,3 | - | - | - | - |
| 2006 |
| 1,3 |
|
|
|
| 2007 |
|
|
| 2,12 | 0,24 |
| 2008 |
|
| 1,041 |
|
|
| 2009 |
|
| 1,071 |
|
|
| 2010 |
|
|
| 1,85 |
|
ЗАДАЧА 129
Рассчитать недостающие показатели динамики
| Год | Пассажирооборот (млр.пасс-км.) | Цепные показатели динамики | |||
| Абсолютный прирост | Темп роста | Темп прироста | Абсолютное значение 1% прироста (млр.пасс.км) | ||
| 2006 | 360,2 | - | - | - | - |
| 2007 |
| 14,5 |
|
|
|
| 2008 |
|
| 1,037 |
|
|
| 2009 |
|
|
|
|
|
| 2010 |
| 10,8 |
|
| 4,018 |
ЗАДАЧА 130
Рассчитать недостающие показатели динамики
| Год | Обьем перевозок (млн.тонн) | Цепные показатели динамики | ||
| Абсолютный прирост | Темп роста | Темп прироста | ||
| 2006 | 520,6 | - | - | - |
| 2007 |
|
| 105,4 |
|
| 2008 |
| -9 |
| 5,8 |
| 2009 |
|
|
|
|
| 2010 |
| 26,4 |
|
|
| 2011 |
|
| 101,7 |
|
ЗАДАЧА 131
Рассчитать недостающие показатели динамики
| Год | Принято студентов, тыс.чел. | Цепные показатели динамики | |||
| Абсолютный прирост | Темп роста % | Темп прироста | Абсолютное значение 1% прироста (млр.пасс.км) | ||
| 2005 | 2791 | - | - | - | - |
| 2006 |
| 146 |
|
|
|
| 2007 |
|
| 106,2 |
|
|
| 2008 |
|
|
| 9,5 |
|
| 2009 |
|
|
|
|
|
| 2010 |
| 475 |
|
| 35,98 |
ЗАДАЧА 132
Рассчитать недостающие показатели динамики
| Год | Производство продукции, млн.руб. | Цепные показатели динамики | |||
| Абсолютный прирост | Темп роста % | Темп прироста | Абсолютное значение 1% прироста (млр.пасс.км) | ||
| 2005 | 92,5 | - | - | - | - |
| 2006 |
| 4,8 |
|
|
|
| 2007 |
|
| 104 |
|
|
| 2008 |
|
|
| 5,8 |
|
| 2009 |
|
|
|
|
|
| 2010 |
| 7 |
|
| 1,15 |
Тема: Метод аналитического выравнивания и прогнозирования
ЗАДАЧА 133
Рассчитать интервальный прогноз объема перевозок на 2010 год, используя линейную трендовую модель по следующим данным, для вероятности Р=0,95:
| Год | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Среднее расстояние перевозки км. | 480 | 508 | 542 | 571 | 604 |
|
ЗАДАЧА 134
Рассчитать интервальный прогноз выпуска продукции на 2011 год, используя линейную трендовую модель по следующим данным , для вероятности Р=0,95:
| Год | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| Выпуск продукции, млн.руб. | 221 | 235 | 272 | 285 | 304 | 340 | 360 | 371 |
|
ЗАДАЧА 135
Рассчитать интервальный прогноз розничного товарооборота на 2011 год, используя линейную трендовую модель по следующим данным , для вероятности Р=0,95:
| Год | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| Розничный товарооборот, млн.руб | 480 | 500 | 540 | 570 | 580 | 590 |
|
ЗАДАЧА 136
Рассчитать интервальный прогноз товарооборота овощей и фруктов на 2011 год, используя линейную трендовую модель по следующим данным , для вероятности Р=0,95:
| Год | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| Продажа, тыс.т. | 100 | 120 | 133 | 160 | 200 | 251 |
|
Тема: Расчет индексов сезонности
ЗАДАЧА 137
Рассчитать индексы сезонности и построить диаграмму волны сезонности по следующим данным:
| Месяц | Среднесуточный объем перевозок | ||
| 2008 | 2009 | 2010 | |
| 1 | 10,2 | 10,7 | 10,3 |
| 2 | 10,4 | 10,4 | 10,6 |
| 3 | 10,6 | 10,8 | 10,9 |
| 4 | 11,0 | 11,1 | 11,3 |
| 5 | 11,3 | 11,2 | 11,2 |
| 6 | 11,5 | 11,0 | 11,7 |
| 7 | 11,6 | 11,3 | 11,8 |
| 8 | 12,0 | 11,7 | 12,4 |
| 9 | 11,2 | 11,6 | 11,7 |
| 10 | 10,9 | 10,7 | 11,2 |
| 11 | 10,2 | 10,4 | 10,8 |
| 12 | 10,0 | 10,3 | 10,5 |
ЗАДАЧА 138
Рассчитать индексы сезонности и построить диаграмму волны сезонности по следующим данным:
| Месяц | Количество браков заключенных в г.Тамбове | ||
| 2008 | 2009 | 2010 | |
| 1 | 173 | 183 | 178 |
| 2 | 174 | 185 | 179 |
| 3 | 167 | 162 | 161 |
| 4 | 142 | 160 | 184 |
| 5 | 137 | 143 | 151 |
| 6 | 145 | 150 | 156 |
| 7 | 153 | 167 | 177 |
| 8 | 171 | 173 | 181 |
| 9 | 143 | 150 | 157 |
| 10 | 162 | 165 | 174 |
| 11 | 178 | 181 | 193 |
| 12 | 185 | 189 | 197 |
Экономические индексы
7.1 Методические указания
Индексом в статистике называется относительный показатель, характеризующий изменение величины какого-либо явления по сравнению с эталоном.
Таблица – Обозначения индексируемых величин
| Обозначение | Индексируемая величина | Обозначение | Индексируемая величина | |
| q | количество (объем) какого-либо товара в натуральном выражении | t | затраты времени на производство единицы продукции, трудоемкость | |
| p | цена единицы товара | W | выработка продукции в единицу времени или на одного работника (производительность труда) | |
| pq | товарооборот (стоимость продукции) | |||
| z (c) | себестоимость единицы продукции | T=tq | общие затраты времени на производство продукции или численность работников | |
| y | урожайность отдельных сельскохозяйственных культур | |||
| П | посевная площадь под отдельными культурами |
Общие индексы количественных показателей
Индекс физического объема продукции показывает относительное изменение стоимости продукции из-за изменения объема производства.
Индивидуальный индекс: 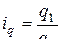 , (7.1)
, (7.1)
Агрегатный индекс: 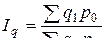 , (7.2)
, (7.2)
где q1 и q0 – объем выпуска продаж в базисном и отчетном периодах соответственно;
p0 – цена в базисном периоде.
Индекс товарооборота (или стоимости продукции), показывает во сколько раз изменилась стоимость продукции.
Агрегатный индекс товарооборота
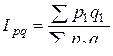 . (7.4)
. (7.4)
На сколько изменилась стоимость продукции показывает разница между числителем и знаменателем индекса:
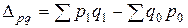 . (7.3)
. (7.3)
При построении индекса физического объема продукции в качестве соизмерителей (весов) принимаются сопоставимые, неизменные, фиксированные цены, отличающиеся от текущих (действующих) цен (это в условиях инфляции могут быть цены предшествующего периода) или себестоимость продукции z0. В этом случае индекс характеризует изменение издержек производства.
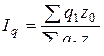 . (7.5)
. (7.5)
Аналогично строятся индексы товарооборота и потребления.
Значение общего индекса Ipq зависит от изменения двух индексируемых величин объема продукции (q0, q1) и цен (p1,p0).
В зависимости от вида исходных данных можно исчислить средние взвешенные (арифметические) индексы физического объема.
Если неизвестно q1, но дано значение q0 и 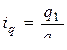 , а также стоимость продукции базисного периода p0, то средний арифметический индекс физического объема равен:
, а также стоимость продукции базисного периода p0, то средний арифметический индекс физического объема равен:
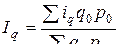 . (7.6)
. (7.6)
Средний гармонический индекс физического объема используется для аналитических оценок в случае, когда неизвестно q0, но дано значение q1 и 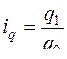 , а также стоимость продукции базисного периода p0:
, а также стоимость продукции базисного периода p0:
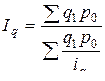 . (7.7)
. (7.7)
Индекс физического объема в прошлом вычисляется в сопоставимых, фиксированных ценах и отражает динамику выпуска продукции. В торговле чаще вычисляется в фактических ценах, отражая одновременное изменение цен и объема.
Дата: 2018-12-21, просмотров: 463.
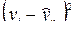
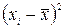

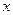
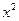
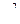
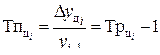 (6.6)
(6.6)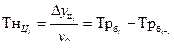 (6.7)
(6.7)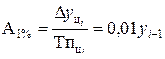 (6.8)
(6.8)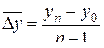 =
= 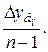 (6.9)
(6.9)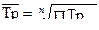
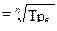
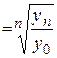 (6.10)
(6.10)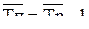 (6.11)
(6.11)