| Номер предприятия | Объем реализации, тыс.руб. | Объем реализации на 1 работника, тыс.руб./чел. | Рентабельность, % | Доля рабочих в общей численности работников, % | Среднемесячная зарплата на 1 работника, руб./чел. |
| 1 | 362728 | 1242 | 26,3 | 74,3 | 5420 |
| 2 | 257206 | 989 | 27,3 | 71,4 | 4456 |
| 3 | 257721 | 1227 | 21,7 | 72,3 | 4681 |
| 4 | 224238 | 901 | 20,6 | 73,9 | 3574 |
Решение: 1) Среднее значение реализованной продукции на одного работника определю по формуле 2.12 средней гармонической взвешенной: 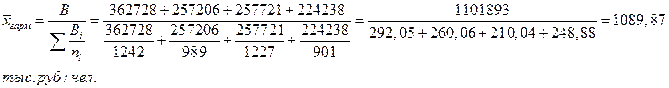
2) Среднее значение производительности труда определяется по формуле 2.10 средней арифметической простой:
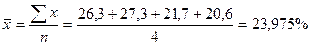
3) Среднее значение заработной платы определяется по формуле 2.11 средней арифметической взвешенной: 
Тема: расчет моды
ЗАДАЧА 23
Распределение проданной обуви по размерам характеризуется следующими показателями:
| Размер обуви | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | и выше |
| Число пар в % к итогу | - | 1 | 6 | 8 | 22 | 30 | 20 | 11 | 1 | 1 | - |
В этом ряду распределения мода равна 41. Именно этот размер обуви пользовался наибольшим спросом покупателей – 30% проданной обуви.
ЗАДАЧА 24
Распределение предприятий по численности промышленно-производственного персонала характеризуются следующими данными:
| Группы предприятий по числу работающих, чел. | Число предприятий |
| 100-200 | 1 |
| 200-300 | 3 |
| 300-400 | 7 |
400-500
30
500-600
19
600-700
15
700-800
5
Итого
80
Модальным интервалом является интервал с наибольшей частотой. В данной задаче он равен 30.
Мода вычисляется по формуле 2.20. Определим значения для расчета моды:
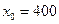
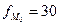

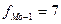
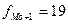 подставим эти значении в формулу моды и произведем вычисления:
подставим эти значении в формулу моды и произведем вычисления:
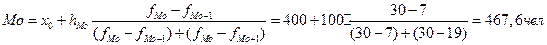
Тема: расчет медианы
ЗАДАЧА 25
Определить медиану заработной платы рабочих
| Месячная заработная плата (тыч.руб) | Число рабочих | Сумма накопленных частот |
| 10 | 2 | 2 |
| 12 | 6 | 8 |
| 15 | 16 | 24 |
| 17 | 12 | - |
| 20 | 4 | - |
|
| 40 |
|
Для определения медианы рассчитаем накопленную сумму частот. Считать будем до тех пор, пока сумма частот не превысит половину общей суммы частот. Для нашей задачи это
24 > 40/2. Варианта соответствующая этой сумме, т.е 15 тыс.руб. и есть медиана ряда.
ЗАДАЧА 26
Рассчитать медиану в интервальном вариационном ряду.
| Группы предприятий по числу работающих, чел. | Число предприятий | Сумма накопленных частот |
| 100-200 | 1 | 1 |
| 200-300 | 3 | 4 |
| 300-400 | 7 | 11 |
| 400-500 | 30 | 41 |
| 500-600 | 19 | - |
| 600-700 | 15 | - |
| 700-800 | 5 | - |
|
| 80 |
|
Определим медианный интервал. В данной задаче сумма накопленных частот, превышающих половину всех значений (41), соответствует интервалу (400-500). Это и есть медианный интервал в котором находится медиана. Определим ее значение по формуле 2.18. При этом значения будут равны:
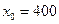
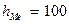
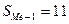
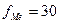
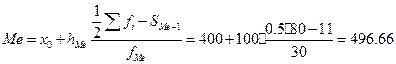
Контрольные задачи
Тема: Пересчет абсолютных величин в условные единицы измерения
ЗАДАЧА 27
В отчетном периоде на производственные нужды израсходованы
следующие виды топлива: мазут топочный – 800 т, угол донецкий – 460 т, газ
природный – 940 тыс.м3 .
На основе приведенных данных определите общий размер потребленного в
отчетном периоде топлива в условных единицах измерения.
Примечание. Средние калорийные эквиваленты для перевода отдельных видов топлива в
условное топливо:
Вид топлива Калорийные эквиваленты
Уголь донецкий, т 0,9
Мазут топочный, т 1,37
Газ природный, тыс.м3 1,2
ЗАДАЧА 28
Выплавка чугуна по цехам завода в отчетном периоде характеризуется
следующими данными:
| Вид чугуна | Количество, тыс.т. |
| Передельный | 52 |
| Литейный | 76 |
| Ванадиевый | 94 |
| Ковкий и валкий | 110 |
| Хромоникелевый | 126 |
| Зеркальный | 124 |
Определите общий объем выплавки чугуна в натуральном выражении и в условном
натуральном выражении (в переводе на передельный чугун). Объясните разницу в
исчисленных показателях объемы выпуска продукции.
Примечание. Для перевода отдельных видов чугуна в условные натуральные единицы измерения
используются следующие коэффициенты:
| Вид чугуна | Коэффициент. |
| Передельный | 1,00 |
| Литейный | 1,15 |
| Ванадиевый | 1,35 |
| Ковкий и валкий | 1,15 |
| Хромоникелевый | 1,50 |
| Зеркальный | 1,50 |
ЗАДАЧА 29
В отчетный период поставка молочной продукции в торговую сеть характеризуется следующими данными:
| Вид продукции | Обьем поставки |
| Молоко 3.2% | 144,0 |
| Молоко 6.0% | 107,0 |
| Кефир | 37,0 |
| Иогурт | 12,0 |
| Ряженка | 6,2 |
| Сметана | 113,0 |
| Творог | 43,0 |
| Сырковая масса | 3,0 |
Требуется определить общий объем поставки молочной продукции торговой сети города в отчетном периоде. Цельномолочная продукция исчисляется в единицах массы путем пересчета каждой единицы молочной продукции на молоко по установленным коэффициентам:
| Вид продукции | Коэффициент |
| Молоко 3.2% | 1,0 |
| Молоко 6.0% | 2,0 |
| Кефир | 1,0 |
| Иогурт | 1,2 |
| Ряженка | 2,0 |
| Сметана | 8,5 |
| Творог | 6,5 |
| Сырковая масса | 5,4 |
Тема: относительные показатели динамики
ЗАДАЧА 30
Имеются следующие данные о потреблении основных продуктов питания на душу населения в год (кг):
Таблица 2.2
| Продукты питания | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Мясо и мясопродукты в пересчете на мясо | 40,3 | 43,7 | 46,3 | 47,8 | 52 | 57 |
| Молоко и молочные продукты в пересчете на молоко | 154 | 172 | 240 | 251 | 307 | 316 |
| Сахар | 34 | 35,8 | 36,1 | 37,5 | 38,8 | 40,9 |
| Овощи и бахчевые | 40 | 51 | 70 | 72 | 82 | 89 |
Определить относительные величины динамики характеризующие рост потребления мяса и мясопродуктов: 1) по сравнению с уровнем 2005 года 2) по сравнению с уровнем предыдущего года. Полученные результаты изобразить графически. Сделать выводы.
ЗАДАЧА 31
По данным задачи 30 определить относительные величины динамики характеризующие рост потребления молока и молочных продуктов: 1) по сравнению с уровнем 2005 года 2) по сравнению с уровнем предыдущего года. Полученные результаты изобразить графически. Сделать выводы.
ЗАДАЧА 32
По данным задачи 30 определить относительные величины динамики характеризующие рост потребления сахара: 1) по сравнению с уровнем 2005 года 2) по сравнению с уровнем предыдущего года. Полученные результаты изобразить графически. Сделать выводы.
ЗАДАЧА 33
По данным задачи 30 определить относительные величины динамики характеризующие рост потребления овощей и бахчевых: 1) по сравнению с уровнем 2005 года 2) по сравнению с уровнем предыдущего года. Полученные результаты изобразить графически. Сделать выводы.
Тема: относительный показатель структуры
ЗАДАЧА 34
Имеются следующие данные о затратах на производство продукции металлургического и машиностроительного заводов:
| Виды затрат | Металлургический завод | Машиностроительный завод |
| Сырье и основные материалы | 25,1 | 47,3 |
| Вспомогательные материалы | 2,6 | 3,3 |
| Топливо | 4,9 | 1,2 |
| Энергия | 1,7 | 1,8 |
| Амортизация | 3,1 | 3,7 |
| Заработная плата и отчисления | 5,3 | 21,8 |
| Прочие расходы | 1,3 | 2,9 |
| Итого | 44 | 82 |
Определите относительные величины структуры затрат на производство продукции на 1)металлургическом заводе 2) машиностроительном заводе. Изобразите полученные структурные величины в виде круговой диаграммы. Сделайте выводы.
ЗАДАЧА 35
Получены следующие данные по Тамбовской области о составе площадей занятыми под плодово-ягодными насаждениями в 2009 году (тыс.га)
| Виды насаждений | Агрофирмы, фермерские хозяйства | Личные подсобные хозяйства населения |
| Плодовые насаждения в том числе: | 19,3 | 25,7 |
| семечковые | 18,6 | 19,0 |
| косточковые | 0,7 | 6,7 |
| Ягодные насаждения | 2,1 | 4,0 |
| Итого | 40,7 | 55,4 |
Определить относительные величины структуры площадей, занятых под плодово-ягодные насаждения в 1) агрофирмах и фермерских хозяйствах 2) личных подсобных хозяйствах. Изобразить полученные структурные величины в виде круговой диаграммы. Сделать выводы.
Тема: Относительный показатель структуры и координации
ЗАДАЧА 36
На предприятии в начале года по списку числилось рабочих 2145 человек, административно-управленческого персонала 147 человек. К концу года списочная численность рабочих увеличилась на 49 человек, а численность административно-управленческого аппарата была сокращена на 4 человека. Определите относительные величины характеризующие соотношения между списочной численностью рабочих и численностью административно-управленческого аппарата на 1) начало года 2) конец года.
Тема: Относительные показатели плана и реализации плана
ЗАДАЧА 37
По плану завод должен был выпускать в отчетном периоде товарной продукции на 12 млрд.руб. при средней численности работающих 4200 человек. Фактически выпуск товарной продукции в этот период составил 13,1 млрд.руб. при средне-списочной численности работающих 4320 человек. Определить 1) относительную величину выполнения плана по выпуску товарной продукции 2) относительную величину выполнения плана по численности работающих 3) показатель изменения фактического выпуска продукции на одного работающего по сравнению с планом.
Тема: Расчет средней арифметической взвешенной для интервального ряда
распределения
ЗАДАЧА 38
При обследовании 50 членов семей рабочих и служащих установлено следующее количество членов семьи: 5; 3; 2; 1; 4; 6; 3; 7; 9; 1; 3; 2; 5; 6; 8; 2; 5; 2; 3; 6; 8; 3; 4; 4; 5; 6; 5; 4; 7; 5; 6; 4; 8; 7; 4; 5; 7; 8; 6; 5; 7; 5; 6; 6; 7; 3; 4; 6; 5; 4. Составьте вариационный ряд распределения частот. Постройте полигон распределения частот, кумуляту. Определите среднее число членов семьи.
Объясните полученные результаты, сделайте выводы.
ЗАДАЧА 39
Имеются данные о еженедельном количестве проданных компьютеров одной из фирм: 398, 412, 560, 474, 544, 690, 587, 600, 613, 457, 504, 477, 530, 641, 359, 566, 452, 633, 474, 499. 580, 606, 344, 455,505, 396, 347, 441, 390, 632, 400, 582. Составьте вариационный ряд. Найдите среднее количество проданных компьютеров.
ЗАДАЧА 40
Администрацию магазина интересует частота покупок калькуляторов. Менеджер в течении января регистрировал данные о покупке МК и собрал следующие данные: 8, 4, 4, 9, 3, 3, 1, 2, 0, 4, 2, 3, 5, 7, 10, 6, 5, 7, 3, 2, 9, 8, 1, 4, 6, 5, 4, 2, 1, 0, 8. Постройте вариационный ряд, найдите среднее количество проданных калькуляторов . Какие рекомендации вы дали бы администрации универсама?
ЗАДАЧА 41
Число пассажиров одного из рейсов за 30 дней составило: 128, 121, 134, 118, 123, 109, 120, 116, 125, 128, 121, 129, 130, 131, 127, 119, 114, 124, 110, 126, 134, 125, 128, 123, 128, 133, 132, 136, 134, 129. Составьте вариационный ряд. Найдите среднее число пассажиров в рейсе? Сделайте анализ полученных результатов.
ЗАДАЧА 42
Имеются данные о годовой мощности предприятий в 2010 году
| Предприятия с годовой мощностью, тыс.т | Количество предприятий |
| До 500 | 27 |
| 500 – 1000 | 11 |
| 1000 – 2000 | 8 |
| 2000 – 3000 | 8 |
| Свыше 3000 | 2 |
Постройте гистограмму, кумуляту. Рассчитайте среднюю мощность предприятий. Сделайте анализ полученных результатов.
ЗАДАЧА 43
По данным выборочного обследования получено следующее распределение по среднедушевому доходу:
| Среднедушевой доход семьи в месяц, у.е. | до 250 | 250– 500 | 500– 750 | 750– 1000 | 1000– 1250 | 1250– 1500 | 1500 и выше |
| Количество обследованных семей | 46 | 236 | 250 | 176 | 102 | 78 | 12 |
Постройте гистограмму, кумуляту. Рассчитайте среднюю мощность предприятий. Сделайте анализ полученных результатов.
ЗАДАЧА 44
Постройте гистограмму частот, найдите среднюю заработную плату работников одного из цехов ОАО «Пигмент»
| Заработная плата, у.е | 500- 750 | 750 – 1000 | 1250 – 1500 | 1500 – 1750 | 1750 – 2000 | 2000 - 2250 |
| Число работников | 12 | 23 | 37 | 19 | 15 | 9 |
ЗАДАЧА 45
Продажа акций на аукционе характеризуется следующими данными:
| Продажа акций в % | 9 - 15 | 15 – 21 | 21 – 27 | 27 – 33 |
| Число акционерных обществ | 3 | 5 | 4 | 2 |
Постройте гистограмму распределения частот. Найдите средний процент продажи акций.
ЗАДАЧА 46
Для оценки состояния деловой активности предприятий были проведены обследования и получены следующие результаты:
| Показатель деловой активности | 0 – 8 | 8 – 16 | 16 – 24 | 24 - 32 |
| Число предприятий | 10 | 15 | 8 | 5 |
Постройте гистограмму распределения частот. Найдите среднее значение показателя деловой активности. Сделайте анализ полученных результатов.
ЗАДАЧА 47
Имеются данные о возрастном составе безработных по РФ:
| Возраст | 16-20 | 20-24 | 25-29 | 30-49 | 50-54 | 55-59 | 60-65 |
| Мужчины | 7,7 | 17,0 | 11,9 | 50,9 | 4,2 | 5,7 | 2,6 |
| Женщины | 11,2 | 18,5 | 11,7 | 49,5 | 4,0 | 3,8 | 1,3 |
Найдите средний возраст безработных мужчин и женщин. Оцените различия показателей возрастного состава безработных мужчин и женщин. Сделайте выводы.
Тема: Средняя гармоническая взвешенная
ЗАДАЧА 48
По данным о производстве и среднегодовой выработке на одного рабочего по четырем бригадам определить среднюю производительность труда одного рабочего в среднем по заводу
| Номер бригады | Произведено валовой продукции тыс.руб | Выработка на одного рабочего тыс.руб. |
| 1 | 57 | 1,9 |
| 2 | 46 | 2,0 |
| 3 | 65 | 2,5 |
| 4 | 70 | 2,8 |
Тема: расчет моды и медианы
ЗАДАЧА 49
Рассчитать моду и медиану по следующим данным:
| Влажность % х | Число образцов f |
| до 14 | 20 |
| 14-16 | 30 |
| 16-18 | 25 |
| 18-20 | 15 |
| 20 и более | 10 |
ЗАДАЧА 50
На основе имеющихся данных о распределении предприятий города по объему выпуска продукции определить моду, медиану:
| Группа предприятий по объему выпуска, млн.руб. | Количество предприятий |
| До 40 | 8 |
| 40 - 50 | 10 |
| 50 - 60 | 18 |
| 60 - 70 | 24 |
| 70 - 80 | 22 |
| 80 - 90 | 23 |
| 90 - 100 | 17 |
| Более 100 | 8 |
ЗАДАЧА 51
Супермаркет имеет данные о покупках, совершаемых покупателями за определенный период. Рассчитать моду и медиану.
| Сумма покупки, тыс.руб. | Количество покупок |
| До 100 | 24 |
| 100 - 200 | 28 |
| 200 - 300 | 40 |
| 300 - 400 | 32 |
| 400 - 500 | 26 |
| 500 - 600 | 19 |
ЗАДАЧА 52
Рассчитать моду и медиану по следующим данным:
| Группы предприятий по себестоимости единицы продукции, руб. | Число предприятий |
| 1,6-2,0 | 2 |
| 2,0-2,4 | 3 |
| 2,4-2,8 | 5 |
| 2,8-3,2 | 7 |
| 3,2-3,6 | 10 |
| 3,6-4,0 | 3 |
Показатели вариации
3.1 Методические указания
Вариацией называется изменяемость величины признака. Вариация проявляется в отклонениях от средних и зависит от множества факторов, влияющих на социально-экономическое явление. Вариация бывает случайной и систематической, существует в пространстве и во времени. Показатели вариации делятся на абсолютные и относительные (таблица 3.1).
Таблица 3.1 - Показатели вариации
|
| Показатель | Формула расчета показателя | |
| простой | взвешенный | ||
| Абсолютные | Размах |
| |
| Среднее линейное отклонение | 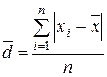 (3.2) (3.2)
| 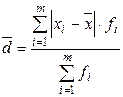 * (3.3) * (3.3)
| |
| Дисперсия | σ2 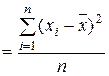 (3.4) (3.4)
| 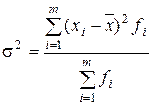 (3.5) (3.5)
| |
| Среднее квадратическое отклонение | 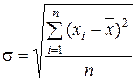 (3.6) (3.6)
| 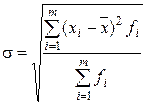 (3.7) (3.7)
| |
| относительные | Коэффициент вариации |
| |
| Линейный коэффициент вариации |
| ||
| Коэффициент осцилляции |
| ||
* – Здесь fi – частота ( 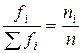 ).
).
Относительные показатели (коэффициент вариации, линейный коэффициент вариации, коэффициент осцилляции) строятся с учетом базы (в виде средней), выражаются в процентах и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации
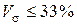 . (3.11)
. (3.11)
Для расчета дисперсии можно использовать модифицированную формулу:
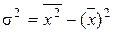 . (3.12)
. (3.12)
Виды дисперсий в совокупности, разделенной на части. Правило сложения дисперсий
Если исходная совокупность является такой, что по значениям признака она делится на l групп, то общая дисперсия складывается из частных дисперсий. В таблице 3.2 представлен анализ такой совокупности.
Таблица 3.2 - Определение исходной совокупности по группам
| Значение признака х | Число единиц в j-й группе | Итого | ||||
| 1 | … | j | … | l | ||
| х1 | f11 | … | f1j | … | f1l | 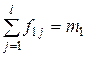
|
| … | … | … | … | … | … | … |
| х i | fi1 | … | fij | … | fil | 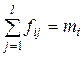
|
| … | … | … | … | … | … | … |
| х k | fk1 | … | fkj | … | fkl | 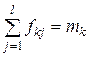
|
| Итого | 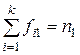
| … | 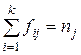
| … | 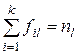
| 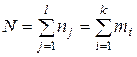
|
Здесь j – номер группы ( 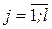 );
);
х i – i-е значение признака ( 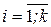 );
);
fij – частота i-го значения признака, число единиц в j-й группе;
mi – сумма частот i-го значения признака в каждой группе;
nj – сумма частот всех значений признака в j-й группе;
N – сумма частот всех значений признака во всех группах (объем совокупности).
Сначала вычисляем l частных средних ( 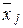 ), т.е. среднее значение признака в каждой группе:
), т.е. среднее значение признака в каждой группе:
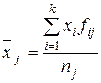 . (3.13)
. (3.13)
На основе частных средних определяем общую среднюю ( 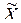 ) по формулам
) по формулам
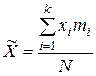 или
или 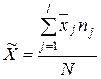 . (3.14)
. (3.14)
Общая дисперсия совокупности
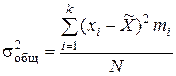 . (3.15)
. (3.15)
Общая дисперсия отражает вариацию признака за счет всех факторов, действующих в данной совокупности.
Вариацию между группами за счет признака-фактора, положенного в основу группировки, отражает межгрупповая дисперсия, которая исчисляется как средний квадрат отклонений групповой средней от общей средней:
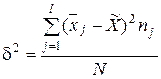 . (3.16)
. (3.16)
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, т.е. вариацию между группами за счет признака-фактора, положенного в основу группировки.
Вариацию внутри каждой группы изучаемой совокупности отражает внутригрупповая дисперсия, которая исчисляется как средний квадрат отклонений значений признака х от частной средней 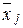 :
:
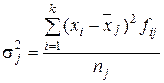 или
или 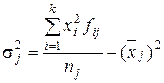 . (3.17)
. (3.17)
Для всей совокупности внутригрупповую вариацию будет выражать средняя из внутригрупповых дисперсий, которая рассчитывается как средняя арифметическая из внутригрупповых дисперсий:
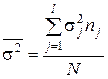 . (3.18)
. (3.18)
Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основу группировки.
Между представленными видами дисперсий существует определенное соотношение, которое известно как правило сложения дисперсий:
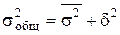 . (3.19)
. (3.19)
Таким образом, общая дисперсия складывается из двух слагаемых: первое – средняя из внутригрупповых дисперсий – измеряет вариацию внутри частей совокупности, второе – межгрупповая дисперсия – вариацию между средними этих частей.
Правило сложения дисперсий позволяет выявить зависимость результатов от определяющих факторов с помощью соотношения межгрупповой и общей дисперсий. Это соотношение называется эмпирическим коэффициентом детерминации (η2) и показывает долю вариации результативного признака под влиянием факторного.
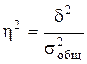 . (3.20)
. (3.20)
Эмпирическое корреляционное отношение (η) показывает тесноту связи между исследуемым явлением и группировочным признаком.
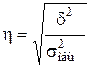 . (3.21)
. (3.21)
η2 и η 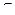 [0, 1]. (3.22)
[0, 1]. (3.22)
Если связь отсутствует, то h = 0. В этом случае межгрупповая дисперсия равна нулю (δ2=0), т.е. все групповые средние равны между собой и межгрупповой вариации нет. Это означает, что группировочный признак не влияет на вариацию исследуемого признака х.
Если связь функциональная, то h = 1. В этом случае дисперсия групповых средних равна общей дисперсии ( 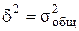 ). Это означает, что группировочный признак полностью определяет характер изменения изучаемого признака.
). Это означает, что группировочный признак полностью определяет характер изменения изучаемого признака.
Чем больше значение корреляционного отношения приближается к единице, тем полнее (сильнее) корреляционная связь между признаками (таблица 3.3).
Таблица 3.3 - Качественная оценка связи между признаками (шкала Чэддока)
Значение 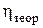
| Характер связи | Значение 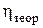
| Характер связи | |
| η = 0 | Отсутствует | 0,5 ≤ η < 0,7 | Заметная | |
| 0 < η < 0,2 | Очень слабая | 0,7 ≤ η < 0,9 | Сильная | |
| 0,2 ≤ η < 0,3 | Слабая | 0,9 ≤ η < 1 | Весьма сильная | |
| 0,3 ≤ η < 0,5 | Умеренная | η = 1 | Функциональная |
3.2 Пример решения задач
Тема: расчет абсолютных и относительных показателей вариации
ЗАДАЧА 53
Супермаркет имеет данные о покупках, совершаемых покупателями за определенный период. Рассчитать абсолютные и относительные показатели вариации. Сделать вывод об однородности исследуемой совокупности.
| Сумма покупки, тыс.руб. | Количество покупок |
| До 100 | 24 |
| 100 - 200 | 28 |
| 200 - 300 | 40 |
| 300 - 400 | 32 |
| 400 - 500 | 26 |
| 500 - 600 | 19 |
Решение: промежуточные данные удобно представить в виде таблицы
Дата: 2018-12-21, просмотров: 934.
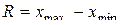 (3.1)
(3.1)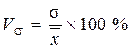 (3.8)
(3.8)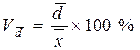 (3.9)
(3.9)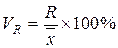 (3.10)
(3.10)