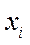
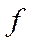
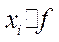
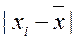
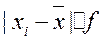
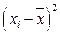
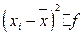
|  
| 
| 
| 
| 
| 
|
| 25 | 110 | 2750 | 12,25 | 1347,5 | 150,0625 | 16506,88 |
| 30 | 175 | 5250 | 7,25 | 1268,75 | 52,5625 | 9198,438 |
| 35 | 290 | 10150 | 2,25 | 652,5 | 5,0625 | 1468,125 |
| 40 | 155 | 6200 | 2,75 | 426,25 | 7,5625 | 1172,188 |
| 45 | 120 | 5400 | 7,75 | 930 | 60,0625 | 7207,5 |
| 50 | 150 | 7500 | 12,75 | 1912,5 | 162,5625 | 24384,38 |
| Итого | 11000 | 37250 | Х | Х | Х | 59937,5 |
Среднее значение выборки:
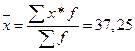
Дисперсия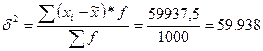 
Средняя ошибка выборки: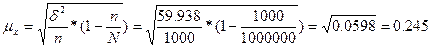 
Тогда средняя дальнобойность имеет вид:
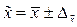; где предельная ошибка равна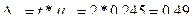 
37,25-0,49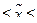 
37,25+0,49 или 36,76 
37,74 т.е. с вероятностью 0,954 можно утверждать что, возможные пределы дальнобойности всей партии патронов лежат в данном диапазоне.
Тема: Определение ошибки выборочной доли при собственно-случайном и механическом отборе
ЗАДАЧА 66
При обследовании 100 образцов изделий отобранных из партии в случайном порядке, оказалось 20 нестандартных. С вероятностью 0,954 определите пределы, в которых находится доля нестандартной продукции в партии.
Рассчитаем долю нестандартной продукции в выборочной совокупности:
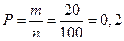Воспользуемся формулой 4.2 для расчета средней ошибки выборочной доли: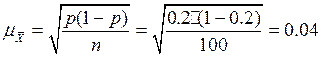 
Предельная ошибка выборочной доли при 0,954 равна:
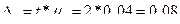тогда
по формуле 4.17 определим верхнюю границу генеральной доли:
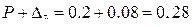
определим нижнюю границу генеральной доли:
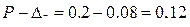
С вероятностью 0,954 можно утверждать, что доля нестандартной продукции в партии товара находится в пределах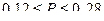 
Тема: Определение необходимой численности выборки при собственно-случайном и механическом отборе
ЗАДАЧА 67
Исходя требований ГОСТа необходимо установить оптимальный размер случайной бесповторной выборки из партии изделий 2000 штук при среднеквадратичном отклонении 15,4 , чтобы с вероятностью 0,997 предельная ошибка не превысила 3% от веса 500 гр. изделия (батона).
Решение.
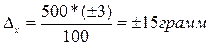
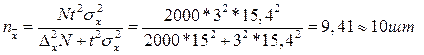
ЗАДАЧА 68
Определите сколько электроламп из всей партии изделий следует подвергнуть обследованию в порядке случайной бесповторной выборки, чтобы с вероятностью 0,954 предельная ошибка не превышала 3% среднего веса спирали (средний вес составляет 42 мг). Коэффициент вариации среднего срока службы компьютеров по данным предыдущих обследований составляет 6%, а вся партия состоит из 1220 электроламп.
Решение: Формула (4.10) оптимальной численности выборки для повторного отбора: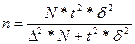 
В этой формуле нам неизвестны три величины: 1.предельная ошибка -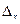 
2. дисперия -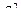 
3. коэффициент t
Определим значение предельной ошибки: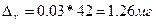 
Среднее квадратичное отклонение найдем из формулы 3.8:
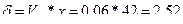тогда 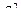= 6,35
коэффициент при Р=0.954 найдем из таблицы 4.1 он равен t=2
N=1220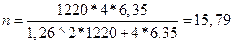 
Таким образом необходимо обследовать 16 электроламп
ЗАДАЧА 69
В районе 10 тыс.семей. Из них 5 тыс. – семьи рабочих, 1 тыс. – семьи служащих, 4 тыс. семьи аграриев. Для определения среднего размера семьи района проектируется типическая выборка
со случайным бесповоротным отбором внутри типических групп. Какое число семей необходимо отобрать, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 0,5 человека, если на основе предыдущих обследований известно, что дисперсия среднего размера семьи в выборке равна 9?
Решение. Рассчитаем необходимую численность типической выборки:
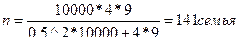
Необходимо отобрать 141 семью из них:
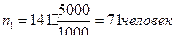из семей рабочих;
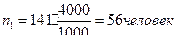из семей служащих;
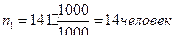из семей аграриев;
Тема: Определение ошибки выборочной средней при серийной выборке
ЗАДАЧА 70
В механическом цехе завода в десяти бригадах работает сто человек. В целях изучения квалификации рабочих была проведена 20% серийная бесповторная выборка, в которую вошли две бригады. Получено следующие распределение, обследованных рабочих по разрядам:
| Рабочие | Разряды рабочих в бригаде 1 | Разряды рабочих в бригаде 2 |
| 1 | 2 | 3 |
| 2 | 4 | 6 |
| 3 | 5 | 1 |
| 4 | 2 | 5 |
| 5 | 5 | 3 |
| 6 | 6 | 4 |
| 7 | 5 | 2 |
| 8 | 8 | 1 |
| 9 | 4 | 3 |
| 10 | 5 | 2 |
Необходимо определить с вероятностью 0,997 пределы в которых находится средний разряд рабочих механического цеха.
Решение. Определим выборочные средние по бригадам и общую среднюю:
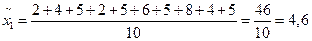
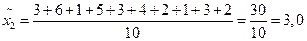
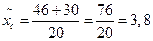
Определим межсерийную дисперсию по формуле 3.17 :
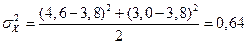
Рассчитаем среднюю ошибку серийной выборки по формуле 4.17
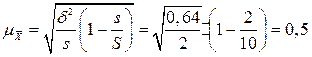
Вычислим предельную ошибку выборки с вероятностью 0,997:
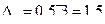
С вероятностью 0,997 можно утверждать, что средний разряд рабочих механического цеха
находится в пределах -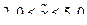 
Контрольные задачи
Тема: Определение ошибки выборочной средней при собственно-случайном и механическом отборе
ЗАДАЧА 71
С целью изучения размеров выручки киосков была произведена 10% -ая случайная бесповторная выборка из 1000 киосков города. В результате были получены данные о средней выручке составившие 50000 руб. В каких пределах с доверительной вероятностью 0,95 может находиться средняя дневная выручка, если среднее квадратическое отклонение составило 15000 руб?
ЗАДАЧА 72
В целях изучения среднедушевого дохода семей города Тамбова, была произведена 1%-я повторная выборка из 30 тыс. семей. По результатам обследования среднедушевой доход семьи в месяц составил 17000 руб. со средним квадратическим отклонением 1500 руб.. С вероятностью 0,95 найдите доверительный интервал, в котором находится величина среднедушевого дохода всех семей города.
ЗАДАЧА 73
Коммерческий банк, изучая возможности предоставления долгосрочных кредитов, опрашивает своих клиентов для определения среднего размера кредита. Из 9706 клиентов опрошено 1000 человек. Среднее значение необходимого кредита в выборке составило 675 у.е. со стандартным отклонением 146 у.е. Найдите границы 95% доверительного интервала для оценки неизвестного среднего значения кредита в генеральной совокупности
ЗАДАЧА 74
В порядке механической выборки было подвержено испытанию на разрыв 100 нитей из партии. В результате обследования установлена средняя крепость пряжи 320 г. при среднеквадратичном отклонении 20 г. С вероятностью 0,954 определить пределы в которых находится средняя крепость пряжи в партии.
ЗАДАЧА 75
Для оценки остаточных знаний по математическим дисциплинам были протестированы 25 студентов 3-го курса групп ЭВМ. Получены следующие результаты в баллах: 107, 90, 114, 88, 117, 110, 103, 120, 96, 122, 93, 100, 121, 110, 135, 85, 120, 89, 100, 126, 90, 94, 99, 116, 111. По этим данным найдите 95%-й интервал для оценки среднего балла тестирования всех студентов 3-го курса.
ЗАДАЧА 76
Среднемесячный бюджет студентов Академии народного хозяйства оценивается по случайной выборке. С вероятностью 0,954 найдите наименьший объём выборки, необходимый для такой оценки. если среднее квадратическое отклонение предполагается равным 200 рублей, а предельная ошибка средней не должна превышать 40 рублей.
ЗАДАЧА 77
На машиностроительном заводе с числом рабочих 5000 человек проведено 4% выборочное обследование квалификации рабочих методом случайного бесповторного отбора.
В результате обследования получены следующие данные:
Квалификация рабочих (тарифные разряды) 1 2 3 4 5 6
Число рабочих 10 30 40 70 30 20
С вероятность 0,997 определить пределы в которых находится средний тарифный разряд рабочих завода.
Тема: Определение ошибки выборочной доли при собственно-случайном и механическом отборе
ЗАДАЧА 78
При выборочном опросе 1200 телезрителей оказалось, что 456 из них регулярно смотрят программы телеканала СТС. Постройте 99%-й доверительный интервал, оценивающий долю всех телезрителей, предпочитающих программы телеканала СТС
ЗАДАЧА 79
Выборочные обследования показали, что доля покупателей, предпочитающих новую модификацию компьютеров, составляет 60% от общего числа покупателей данного товара. Каким должен быть объём выборки, чтобы можно было получить оценку генеральной доли с точностью не менее 0,05 при доверительной вероятности 0,997
ЗАДАЧА 80
С помощью собственно – случайного повторного отбора фирма провела обследование 900 своих служащих. Средний стаж работы в фирме равен 8,7 года, а среднее квадратическое отклонение – 2,7 года. Среди обследованных оказалось 270 женщин. Считая стаж работы служащих распределённым по нормальному закону определите: а) с вероятностью 0,95 доверительный интервал, в котором окажется средний стаж работы всех служащих фирмы; б) с вероятностью 0.997 доверительный интервал, накрывающий неизвестную долю женщин во всём коллективе фирмы
ЗАДАЧА 81
В городе 500 тыс.жителей. По материалам учета городского населения было обследовано
50 тыс.жителей методом случайного бесповторного отбора. В результате обследования установлено, что в городе 15% жителей старше 60 лет. С вероятностью 0,683 определите пределы, в которых находится доля жителей города старше 60 лет.
Тема: Определение необходимой численности выборки при собственно-случайном и механическом отборе
ЗАДАЧА 82
По данным бесповторного выборочного обследования в 2010 году прожиточный минимум населения Северо-Кавказского региона составил в среднем на душу населения 16000 руб. в месяц. Каким должен был быть минимально необходимый объём выборки, чтобы с вероятностью 0,997 можно было утверждать, что этот показатель уровня жизни населения в выборке отличается от своего значения в генеральной совокупности не более чем на 100 рублей, если среднее квадратическое отклонение принять равным 300 рублей
ЗАДАЧА 83
Для определения среднего размера вклада определенной категории вкладчиков в отделениях сберегательного банка города, где число вкладчиков 5000, необходимо провести выборку лицевых счетов методом механического отбора. Предварительно установлено, что среднее квадратическое отклонение размеров вклада составляет 1200 рублей. Определить необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки не превысит 100 рублей.
ЗАДАЧА 84
Среднемесячный бюджет студентов Тамбовского железнодорожного колледжа оценивается по случайной повторной выборке. С вероятностью 0,954 найдите наименьший объём выборки, необходимый для такой оценки. если среднее квадратическое отклонение предполагается равным 100 рублей, а предельная ошибка средней не должна превышать 20 рублей.
ЗАДАЧА 85
В механическом цехе завода 1000 рабочих. Из них 800 квалифицированных и 200 неквалифицированных. С целью изучения производительности труда предполагается провести типическую выборку рабочих с пропорциональным отбором. Отбор внутри групп механический. Какое число рабочих необходимо отобрать, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 6 человек, при среднем квадратичном отклонении 25?
Тема: Определение ошибки выборочной средней при серийной выборке
ЗАДАЧА 86
Изготовленная продукция упаковывается в ящики по 50 шт. Из 500 ящиков поступивших на склад , в порядке случайной бесповторной выборки обследовано 10 ящиков, все детали которых проверены на вес. Результаты проверки показали, что средний вес деталей составил в граммах:
30; 34; 28; 36; 40; 26; 38; 34; 44; 50. Средний вес деталей в выборке составил 32 г.С вероятностью 0,997 определите пределы, в которых находится средний вес деталей, поступивших на слад готовой продукции.
Дата: 2018-12-21, просмотров: 472.
