4.1 Методические указания
Наиболее широко распространенным видом не сплошного наблюдения является выборочное наблюдение, при котором обследуются не все единицы изучаемой совокупности, а лишь определенным образом отобранная их часть.
Вся подлежащая изучению совокупность объектов (наблюдений) называется генеральной совокупностью. Выборочной совокупностью или выборкой называется часть генеральной совокупности, отобранная для изучения свойств обеспечивающая репрезентативность.
Отбор из генеральной совокупности проводится таким образом, чтобы на основе выборки можно было получить достаточно точное представление об основных параметрах совокупности в целом. При этом речь идет как о точечной оценке, в качестве которой принимается соответствующее значение средней, доли и т.д., полученное в результате выборки, так и об интервальной оценке, т.е. о тех пределах, в которых с определенной вероятностью может находиться значение искомого параметра в генеральной совокупности. Главное требование, которому должна отвечать выборочная совокупность, — это требование ее репрезентативности, т.е. представительности.
В статистике результаты сплошного наблюдения иногда оцениваются как выборочные характеристики. Такая трактовка полученных данных имеет место в тех случаях, когда число обследованных единиц невелико и нет твердой уверенности в том, что изучаемые характеристики не могут принимать иных значений, кроме выявленных в результате наблюдения. При проведении экспериментов число значений может быть бесконечно большим, поэтому, формулируя выводы на основе ограниченного их числа, необходимо рассматривать полученные данные как выборочные характеристики.
Распространяя результаты выборочного обследования на генеральную совокупность, следует иметь в виду, что между характеристиками генеральной и выборочной совокупности возможно расхождение, обусловленное тем, что обследуется не, вся совокупность, а лишь ее часть.
Ошибкой статистического наблюдения считается величина отклонения между расчетным и фактическим значениями признаков изучаемых объектов.
Выборочный метод обеспечивает значительную экономию материальных и финансовых ресурсов при проведении статистического наблюдения, что позволяет расширить программу обследования и повысить его оперативность. Второе преимущество – высокая достоверность получаемых данных, так как при относительно небольшом объеме выборки можно организовать эффективный контроль за качеством собираемой информации. Таким образом, снижается вероятность появления ошибок регистрации и не обнаружения их на стадии проверки первичной информации. И наконец, в ряде случаев, когда сплошное наблюдение связано с уничтожением или порчей обследуемых единиц (например, при проверке качества поступающих в продажу продуктов питания), возможно только выборочное обследование.
Точность оценок, полученных на основе выборочного метода, зависит не от доли обследованных единиц, а от их числа.
Основные этапы выборочного наблюдения;
1) определение цели, задач и составление программы наблюдения;
2) формирование выборки;
3) сбор данных на основе разработанной программы;
4) анализ полученных результатов и расчет основных характеристик выборочной совокупности;
5) расчет ошибки выборки и распространение ее результатов на генеральную совокупность.
Различают виды выборки:
1) случайная (собственно-случайная);
2) механическая (например, каждый 10, 20 и т.д.);
3) типическая (стратифицированная), когда генеральная совокупность разбита на группы и в каждой группе обследуются по нескольку объектов));
4) серийная (гнездовая), когда случайным образом отбираются целые серии.
Наиболее простой способ формирования выборочной совокупности – собственно случайный отбор. Теоретические основы выборочного метода, первоначально разработанные применительно к собственно случайному отбору, используют и для определения ошибок выборки при других способах наблюдения.
Собственно случайный отбор может быть повторным и бесповторным. При повторном отборе каждая единица, отобранная в случайном порядке из генеральной совокупности, после проведения наблюдения возвращается в эту совокупность и может быть вновь подвергнута обследованию. На практике такой способ отбора встречается редко. Гораздо более распространен собственно случайный бесповторный отбор, при котором обследованные единицы в генеральную совокупность не возвращаются и не могут быть обследованы повторно. При повторном отборе вероятность попадания в выборку для каждой единицы генеральной совокупности остается неизменной. При бесповторном отборе она меняется, но для всех единиц, оставшихся в генеральной совокупности после отбора из нее нескольких единиц, вероятность попадания в выборку одинакова.
Среднюю ошибку выборки и объем выборки можно вычислить по следующим формулам:
| Наименование показателя | Вид выборки | |
| повторная | бесповторная | |
| Случайная выборка Средняя (стандартная) ошибка | 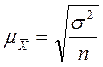 (4,1) (4,1)
| 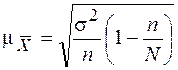 (4,4) (4,4)
|
| Средняя ошибка доли признака | 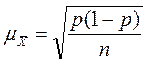 (4,2) (4,2)
| 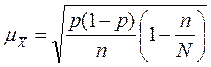 (4,5) (4,5)
|
| Объем выборки | 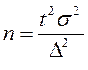 (4,3) (4,3)
| 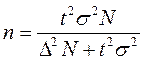 (4,6) (4,6)
|
| Типическая выборка Средняя ошибка | 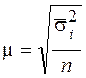 (4,7) (4,7)
| 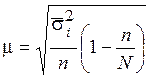 (4,9) (4,9)
|
| Объем выборки | 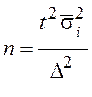 (4,8) (4,8)
| 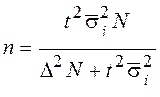 (4,10) (4,10)
|
| Серийная выборка Средняя ошибка | 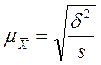 (4,11) (4,11)
| 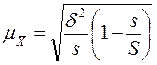 (4,13) (4,13)
|
| Объем выборки |  (4,12) (4,12)
|  (4,14) (4,14)
|
Где:
t – коэффициент доверия
n – объем выборки;
N – объем генеральной совокупности;
s - число отобранных серий;
S – общее число серий;
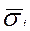 - средняя из групповых дисперсий;
- средняя из групповых дисперсий;
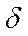 - межгрупповая дисперсия.
- межгрупповая дисперсия.
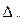 - предельная ошибка выборки
- предельная ошибка выборки 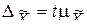 (4,15), т.е. предельная ошибка равна t-кратному числу средних ошибок выборки.
(4,15), т.е. предельная ошибка равна t-кратному числу средних ошибок выборки.
Существуют соотношение связывающее генеральную среднюю 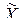 , предельную ошибку выборки
, предельную ошибку выборки 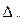 и выборочную среднюю
и выборочную среднюю 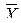 :
:
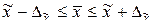 (4,16) или
(4,16) или 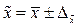 (4,17)
(4,17)
Для выборки объема 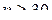 предельная ошибка
предельная ошибка 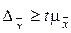 может быть определена из соотношения
может быть определена из соотношения 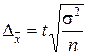 (4,18)
(4,18)
Таблица 4.1
| t | 1,00 | 1,96 | 2,00 | 2,58 | 3,00 |
| F(t) | 0,683 | 0,9500 | 0,9545 | 0,9901 | 0,9973 |
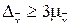 (4,19) – это предел возможной ошибки (правило «трех сигм»).
(4,19) – это предел возможной ошибки (правило «трех сигм»).
F ( t ) – вероятность (или достоверность) выборки
.
Формы организации выборочного наблюдения
Типическая (стратифицированная) выборка: общий список разбивается на отдельные списки (однородной группы). Общий объем выборки n разбивается пропорционально между списками:
1-й вариант
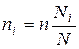 , (4.20)
, (4.20)
где n – объем выборки
N – объем генеральной совокупности
ni – число наблюдений из i-ой типической группы
Ni – объем i-ой типической группы в генеральной совокупности.
2-й вариант – равномерный (из каждой группы поровну)
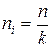 , (4.21)
, (4.21)
где k – число групп.
3-й вариант – оптимальный (для групп с большей вариацией признака объем наблюдений увеличивается)
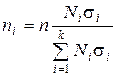 . (4.22)
. (4.22)
4.2 Пример решения задач
Тема: Определение ошибки выборочной средней при собственно-случайном и механическом отборе
ЗАДАЧА 64
Методом случайной повторной выборки было взято для проверки на вес 200 шт.деталей.
В результате был установлен средний вес одной детали 30 гр. при среднем квадратичном отклонении 4 гр. С вероятностью 0,954 требуется определить пределы в которых находится средний вес деталей в генеральной совокупности.
Рассчитаем предельную ошибку выборочной средней (4.18)
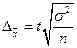 при Р=0,954 значение t=2, тогда
при Р=0,954 значение t=2, тогда 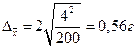
по формуле 4.17 определим верхнюю границу генеральной средней:
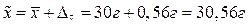
определим верхнюю границу генеральной средней:
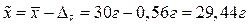
С вероятностью 0,954 можно утверждать, что средний вес детали в генеральной совокупности находится в пределах 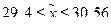
ЗАДАЧА 65
Из партии в 1 млн.шт. мелкокалиберных патронов путем случайного бесповторного отбора взято для определения дальности боя 1000 шт. По результатам испытаний с вероятностью 0,954 определить для всей партии патронов возможные пределы средней дальнобойности
| Дальность боя, м | Число патронов |
| 25 | 110 |
| 30 | 175 |
| 35 | 290 |
| 40 | 155 |
| 45 | 120 |
| 50 | 150 |
промежуточные данные в таблице сведены в таблицу:
Дата: 2018-12-21, просмотров: 396.