1. Выбор группировочного признака – признака, по которому производится разбиение совокупности на отдельные группы. В качестве признака необходимо использовать существенные обоснованные признаки. Группировочный признак – это основание (свойство объекта) для разделения объектов на группы.
Признаки различаются:
· по форме выражения (атрибутивные и количественные);
· по характеру колебания (альтернативные «да», «нет»; множественные);
· по роли во взаимосвязи явлений (результативные – могут меняться в зависимости от ситуации и целей анализа; факторные – воздействующие на другие признаки).
2. Определение количества групп. Если в основание группировки положен атрибутивный признак, то количество групп будет столько, сколько существует градаций (уровней) данного признака. Если основание группировки – количественный признак, то при определении количества групп в каждом конкретном случае следует исходить не только из степени колеблемости признака, но и из особенностей объекта и цели исследования.
Если совокупность состоит из большого числа единиц и распределение единиц по группировочному признаку близко к нормальному, для определения количества групп (m) используют формулу Стерджесса:
m = 1+3,322·lg N, (1.1)
где N – численность единиц совокупности.
Таблица 1.4 - Номограмма по формуле Стерджесса
| N | 15¸24 | 25¸44 | 45¸89 | 90¸179 | 180¸359 | 360¸719 | 720¸1489 |
| m | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
3. Определение интервала группировки. Интервал – это значение варьирующего признака, лежащее в определенных границах.
Если вариация признака происходит в сравнительно узких границах и распределение носит равномерный характер, то строят группировку с равными интервалами:
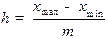, (1.2)
где h – величина интервала;
xmax, xmin – максимальное и минимальное значения группировочного признака в совокупности;
m – число групп.
Величина интервала округляется до ближайшего целого числа, или же кратного 10, 50, 100.
Возможны и другие варианты определения интервала группировки.
Интервалы могут быть двух видов:
· закрытыми, когда у интервала указаны обе границы;
· открытыми, когда у первого интервала указана верхняя граница, а у последнего – нижняя (например, в таблице 2.3, 1-я группа населения по размеру среднедушевого дохода – до 1000 руб.; последняя – 10000 и более).
Возможно построение вторичных группировок. Основные задачи, вторичной группировки:
· приведение данных к сопоставимым результатам;
· укрупнение интервалов;
· долевая перегруппировка (образование новых групп с меньшими интервалами).
1.2 Пример решения задач
Тема: построение группировок
ЗАДАЧА 1
Построить структурную и аналитическую группировку на примере 30 коммерческих банков одного из регионов России - таблица 1.5
Таблица 1.5
Основные показатели деятельности 30 коммерческих банков одного из регионов России на 1 января 2010 года
| № п/п | Сумма активов баланса тыс.руб | Численность занятых человек | Балансовая прибыль тыс.руб |
| 1 | 570 | 95 | 75 |
| 2 | 1050 | 98 | 108 |
| 3 | 6470 | 418 | 2031 |
| 4 | 3910 | 278 | 342 |
| 5 | 2000 | 205 | 283 |
| 6 | 4150 | 302 | 1341 |
| 7 | 1760 | 178 | 186 |
| 8 | 3840 | 270 | 421 |
| 9 | 2330 | 201 | 264 |
| 10 | 5480 | 308 | 1424 |
| 11 | 480 | 72 | 55 |
| 12 | 1120 | 94 | 147 |
| 13 | 3540 | 205 | 345 |
| 14 | 2150 | 144 | 247 |
| 15 | 3780 | 294 | 485 |
| 16 | 4750 | 297 | 1152 |
| 17 | 830 | 87 | 94 |
| 18 | 6940 | 422 | 1980 |
| 19 | 2710 | 198 | 258 |
| 20 | 3660 | 254 | 365 |
| 21 | 3820 | 300 | 334 |
| 22 | 780 | 144 | 125 |
| 23 | 7010 | 500 | 2053 |
| 24 | 2980 | 250 | 300 |
| 25 | 1980 | 184 | 185 |
| 26 | 3120 | 214 | 289 |
| 27 | 580 | 100 | 155 |
| 28 | 2480 | 196 | 197 |
| 29 | 5520 | 350 | 1705 |
| 30 | 3370 | 199 | 320 |
Решение
В качестве группировочного признака возьмем сумму активов баланса и поэтому показателю построим ранжированный ряд от минимального значения до максимального.
Для этого по формуле (1.1) рассчитаем число групп
m = 1+3,322·lg 30 = 5,90 ≈ 6.
Определим интервал группировки по формуле (1.2)
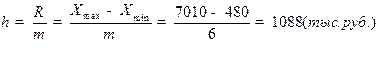
Так как в рассматриваемом примере рассчитанная величина интервала представляет собой четырехзначное число, округлим его до 1100 тыс.руб
Далее обозначим границы групп со следующими интервалами:
· группа 1: до 1600;
· группа 2:1600-2700
· группа 3:2700-3800
· группа 4: 3800-4900
· группа 5:4900-6000
· группа:6600 и более.
| Результаты группировки заносятся в таблицу, определяются общие итоги по совокупности единиц наблюдения по каждому показателю (табл.1.6) Таблица 1.6 Группировка коммерческих банков одного их регионов России по сумме активов баланса на 1 января 2010 г. (итоговая таблица) |
| |||||||
|
| ||||||||
| № п/п | Группы банков по сумме активов баланса тыс.руб. | Число банков, ед. | Сумма активов баланса тыс.руб | Численность занятых человек | Балансовая прибыль тыс.руб | |||
| 1 | до 1600 | 7 | 5410 | 690 | 759 | |||
| 2 | 1600-2700 | 6 | 12700 | 1108 | 1362 | |||
| 3 | 2700-3800 | 7 | 23160 | 1614 | 2362 | |||
| 4 | 3800-4900 | 5 | 20470 | 1447 | 3590 | |||
| 5 | 4900-6000 | 2 | 11000 | 658 | 3129 | |||
| 6 | 6600 и более. | 3 | 20420 | 1340 | 6064 | |||
|
| ||||||||
Итого
30
93160
6857
17266
Таблица 1.7
Структурная группировка коммерческих банков одного их регионов России
по сумме активов баланса на 1 января 2010 г.
№ п/п
Группы банков по сумме активов баланса тыс.руб.
1
до 1600
23,3
5,9
10,1
4,4
2
1600-2700
20,0
13,6
16,2
7,9
3
2700-3800
23,3
24,8
23,5
13,7
4
3800-4900
16,7
22,0
21,1
20,8
5
4900-6000
6,7
11,8
9,6
18,1
6
6600 и более.
10,0
21,9
19,5
35,1
Итого
100
100
100
100
Таблица 1.7 получена на основе таблицы 1.6 путем приведения показателей к 100%.
| Таблица 1.8 Аналитическая группировка коммерческих банков одного их регионов России |
| |||||
| по сумме активов баланса на 1 января 2010 г. |
|
| ||||
| № п/п | Группы банков по сумме активов баланса тыс.руб. | Число банков, ед. | В среднем на один банк | |||
| Сумма активов баланса тыс.руб | Численность занятых человек | Балансовая прибыль тыс.руб | ||||
| 1 | до 1600 | 7 | 773 | 99 | 108 | |
| 2 | 1600-2700 | 6 | 2117 | 185 | 227 | |
| 3 | 2700-3800 | 7 | 3309 | 231 | 337 | |
| 4 | 3800-4900 | 5 | 4094 | 289 | 718 | |
| 5 | 4900-6000 | 2 | 5500 | 329 | 1565 | |
| 6 | 6600 и более. | 3 | 6807 | 447 | 2021 | |
|
|
Итого | - |
3105 |
229 |
576 | |
Соответственно, Таблица 1.8 также получена из Таблицы 1.6 путем усреднения показателей, рассчитанных в среднем на один банк для каждого интервала. Данные табл.1.8 характеризуют взаимосвязь суммы активов баланса, численности занятых работников и балансовой прибыли банков. Чем больше сумма активов баланса банка, тем больше численность его работников и балансовая прибыль. В шестой группе банков средняя численность занятых в 4.5 раза больше, чем в 1 группе, в балансовая прибыль – в 18,7 раза. Следовательно, крупные банки работают эффективнее.
1.3 Инструментальные средства решения задачи
Для решения статистических задач приведенных в методическом пособии мы будем использовать электронные таблицы MS Excel 2003. При этом мы не будем пользоваться дополнительными возможностями MS Excel такими как – встроенными статистическими функциями, пакетом анализа, встроенным языком VBA. Нашим инструментом при решении задач будут – вычисляемые ячейки со встроенными формулами, фильтры, сортировка данных, построение диаграмм. Причина такого сужения набора инструментов пояснена автором в ведении данного методического пособия.
Итак, решение задачи 1 средствами MS Excel состоит из следующих этапов:
1. Перенесем исходную табл.1.5 на лист 1 книги MS Excel
2. Выделим столбец «Сумма активов баланса» (вместе с заголовком) и установим фильтр с помощью цепочки команд – Данные – Фильтр – Автофильтр
3. В установленном фильтре выберем пункт – Условие
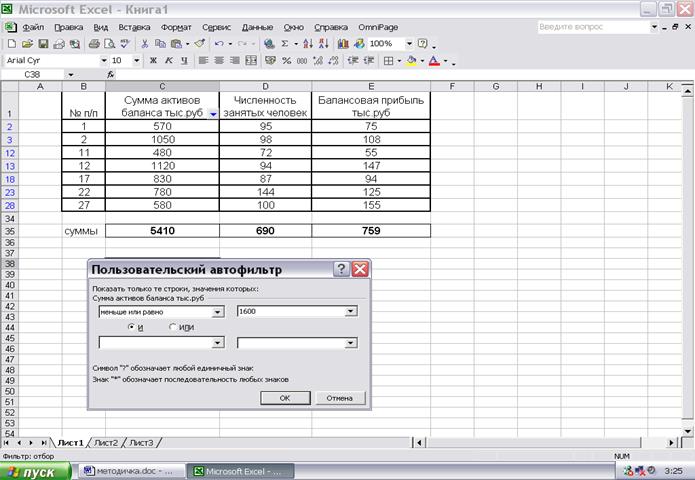4. Смоделируем это условие для первого интервала «до 1600». Результат такого моделирования показан на Рис.1.1
Рис. 1.1 Установка автофильтра
5. Мы видим, что данному условию «меньше или равно 1600» отвечают семь банков из тридцати. Это №№ 1,2,11,12,17,22,27. Нетрудно сложить сумму их активов, численность занятых и балансовую прибыль. Эти цифры и составят первую строку таблицы 1.6.
6. Соответственно, пять следующих строк таблицы 1.6 также можно получить с помощью фильтра. Однако, условие будет другим - «больше 1600 - И - меньше или равно 2700».
7. Не забывайте проверить полученные данные в столбце «число банков» таблицы 1.6. Сумма числа банков должна равняться 30
8. Таблицы 1.7 и 1.8 нетрудно получить, с помощью несложного пересчета таблицы 1.6. Формулы пересчета представлены на Рис. 1.2
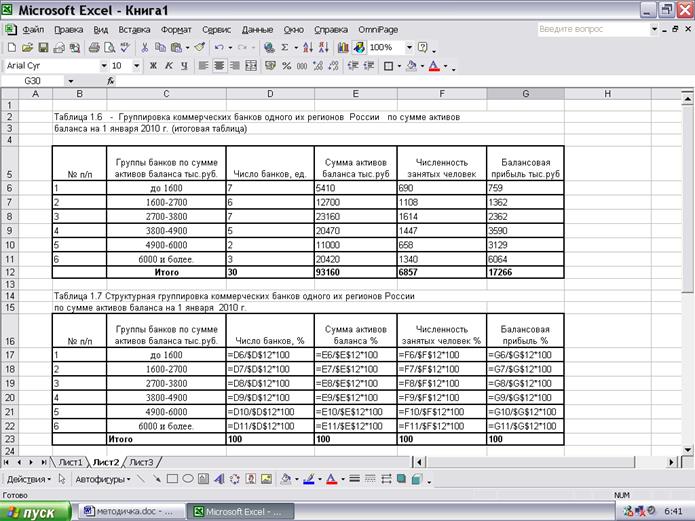
Рис. 1.2 Формулы расчета структурной группировки
Дата: 2018-12-21, просмотров: 329.
