| Сумма покупки, тыс.руб. | 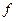
| 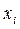
| 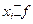
| 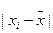
| 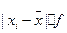
| 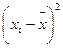
| 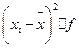
| |
| До 100 | 24 | 50 |
| 238,46 | 5723,04 | 56863,17 | 1364716,12 | |
| 100 - 200 | 28 | 150 | 4200 | 138,46 | 3876,88 | 19171,17 | 536792,80 | |
| 200 - 300 | 40 | 250 | 10000 | 38,46 | 1538,40 | 1479,17 | 59166,86 | |
| 300 - 400 | 32 | 350 | 11200 | 61,54 | 1969,28 | 3787,17 | 121189,49 | |
| 400 - 500 | 26 | 450 | 11700 | 161,54 | 4200,04 | 26095,17 | 678474,46 | |
| 500 - 600 | 19 | 550 | 10450 | 261,54 | 4969,26 | 68403,17 | 1299660,26 | |
| Итого | 169 | 48750 | 22276,9 | 175799,03 | 4060000 | |||
| Среднее | 288,46 | 131,82 | 24023,67 |
Среднее значение вычислим по формуле 2.11- 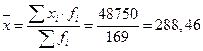
Для расчета модуля разности 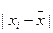 удобно пользоваться встроенной функцией Excel – ABS из категории математические.
удобно пользоваться встроенной функцией Excel – ABS из категории математические.
Рассчитаем показатели, характеризующие вариацию:
Расчет показателей вариации
| Показатель | Формула расчета |
| Размах (3.1) | 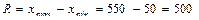
|
| Среднее линейное отклонение (3.2) | 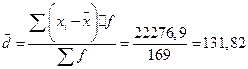
|
| Среднее -квадратичное отклонение (3.3) | 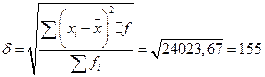
|
| Коэффициент вариации (3.8) | 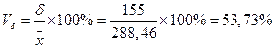
|
| Коэффициент осцилляции (3.10) | 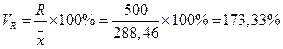
|
| Линейный коэффициент вариации (3.9) | 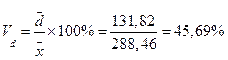
|
Согласно формулы 3.11 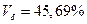 >33% - т.е. исследуемая совокупность неоднородна
>33% - т.е. исследуемая совокупность неоднородна
ЗАДАЧА 54
Рассчитать абсолютные и относительные показатели вариации по исходным данным задачи 53, используя для расчета дисперсии формулу 3.12. Модифицированная формула записывается в следующем виде:
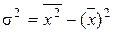 . или
. или 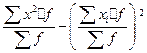
Промежуточные данные удобно представить в таблице:
| Сумма покупки, тыс.руб. | 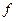
| 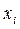
| 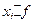
| 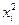
| 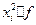
| 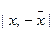
| 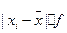
|
| До 100 | 24 | 50 | 1200 | 2500 | 60000 | 238,46 | 5723,04 |
| 100 - 200 | 28 | 150 | 4200 | 22500 | 630000 | 138,46 | 3876,88 |
| 200 - 300 | 40 | 250 | 10000 | 62500 | 2500000 | 38,46 | 1538,40 |
| 300 - 400 | 32 | 350 | 11200 | 122500 | 3920000 | 61,54 | 1969,28 |
| 400 - 500 | 26 | 450 | 11700 | 202500 | 5265000 | 161,54 | 4200,04 |
| 500 - 600 | 19 | 550 | 10450 | 302500 | 5747500 | 261,54 | 4969,26 |
| Итого | 169 | 48750 | 715000 | 18122500 | 22276,9 | ||
| Среднее | 288,46 | 131,82 |
Тогда 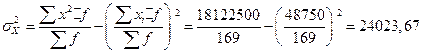
и 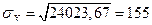 .
.
Все остальные показатели вариации считаются аналогично задачи 53.
Тема: расчет групповой, межгрупповой и общей дисперсии (по правилу сложения дисперсий)
ЗАДАЧА 55
Определим групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным о производительности труда в двух бригадах:
| Изготовлено | Количество рабочих, | |
| в бригаде 1 | в бригаде 2 | |
| х i | fi1 | fi2 |
| 10 | 1 | 0 |
| 12 | 3 | 0 |
| 14 | 3 | 1 |
| 16 | 2 | 3 |
| 18 | 1 | 2 |
| 20 | 0 | 4 |
Промежуточные расчеты занесем в таблицы:
| х i | Бр. 1 | Бр. 2 | mi | Промежуточные расчеты для | ||
| fi1 | fi2 | х i · fi1 | х i · fi2 | х i · mi | ||
| 10 | 1 | 0 | 1 | 10 | 0 | 10 |
| 12 | 3 | 0 | 3 | 36 | 0 | 36 |
| 14 | 3 | 1 | 4 | 42 | 14 | 56 |
| 16 | 2 | 3 | 5 | 32 | 48 | 80 |
| 18 | 1 | 2 | 3 | 18 | 36 | 54 |
| 20 | 0 | 4 | 4 | 0 | 80 | 80 |
| Σ | n1=10 | n2=10 | N=20 | Σх i · fi1=138 | Σх i · fi2=178 | Σх i · mi =316 |
| х i | Промежуточные расчеты для определения дисперсий | |||||
| (х i – | (х i – | (х i – | (х i – | (х i – | (х i – | |
| 10 | -3,8 | -7,8 | -5,8 | 14,44 | 0,00 | 33,64 |
| 12 | -1,8 | -5,8 | -3,8 | 9,72 | 0,00 | 43,32 |
| 14 | 0,2 | -3,8 | -1,8 | 0,12 | 14,44 | 12,96 |
| 16 | 2,2 | -1,8 | 0,2 | 9,68 | 9,72 | 0,20 |
| 18 | 4,2 | 0,2 | 2,2 | 17,64 | 0,08 | 14,52 |
| 20 | 6,2 | 2,2 | 4,2 | 0,00 | 19,36 | 70,56 |
| Σ | – | – | – | 51,60 | 43,60 | 175,20 |
Средняя производительность труда для 1-й бригады:
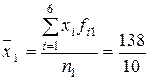 = 13,8 шт./ч.
= 13,8 шт./ч.
Средняя производительность труда для 2-й бригады:
 = 17,8 шт./ч.
= 17,8 шт./ч.
Средняя производительность труда для 1-й и 2-й бригады:
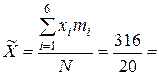
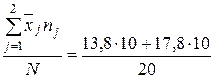 = 15,8 шт./ч.
= 15,8 шт./ч.
| Дисперсия 1-й группы (бригады)
| Дисперсия 2-й группы (бригады)
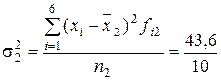 = 4,36 = 4,36
| |
| Средняя из групповых дисперсий
| Межгрупповая дисперсия
| |
| Общая дисперсия |
| |
| Проверка по правилу сложения дисперсий: |
| |
Эмпирический коэффициент детерминации:
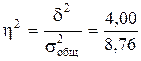 = 0,457 = 45,7%.
= 0,457 = 45,7%.
Отсюда можно сделать вывод, что общая вариация производительности труда на 45,7% обусловлена вариацией между группами.
Эмпирическое корреляционное отношение
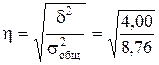 = 0,6757.
= 0,6757.
Значение h = 0,6757 показывает заметную связь по шкале Чэддока (см. таблицу 3.3) между исследуемым явлением (производительностью труда) и группировочным признаком (бригады).
Контрольные задачи
Тема: расчет абсолютных и относительных показателей вариации
ЗАДАЧА 56
Известна структура посевных площадей агрофирмы. Рассчитать абсолютные и относительные показатели вариации. Сделать вывод об однородности исследуемой совокупности.
| Урожайность пшеницы, ц/га | Посевная площадь, га |
| 14-16 | 100 |
| 16-18 | 300 |
| 18-20 | 400 |
| 20-22 | 200 |
ЗАДАЧА 57
По условиям задачи 56 рассчитать абсолютные и относительные показатели вариации. Сделать вывод об однородности исследуемой совокупности. Для расчета дисперсии использовать
формулу 3.12.
ЗАДАЧА 58
Известна структура посевных площадей агрофирмы. Рассчитать абсолютные и относительные показатели вариации. Сделать вывод об однородности исследуемой совокупности.
| Урожайность хлопка-сырца, ц/га | Посевная площадь, в % к итогу |
| 10-14 | 18 |
| 14-18 | 18 |
| 18-22 | 25 |
| 22-26 | 25 |
| 26-30 | 13 |
| 30-34 | 1 |
| итого | 100 |
ЗАДАЧА 59
По условиям задачи 58 рассчитать абсолютные и относительные показатели вариации. Сделать вывод об однородности исследуемой совокупности. Для расчета дисперсии использовать
формулу 3.12.
ЗАДАЧА 60
Рассчитать абсолютные и относительные показатели вариации. Сделать вывод об однородности исследуемой совокупности.
| Затраты времени на одну деталь, в мин. | Число рабочих в % к итогу |
| 22-24 | 2 |
| 24-26 | 12 |
| 26-28 | 34 |
| 28-30 | 40 |
| 30-32 | 10 |
| 32-34 | 2 |
| итого | 100 |
ЗАДАЧА 61
По условиям задачи 60 рассчитать абсолютные и относительные показатели вариации. Сделать вывод об однородности исследуемой совокупности. Для расчета дисперсии использовать
формулу 3.12.
Тема: расчет групповой, межгрупповой и общей дисперсии
(по правилу сложения дисперсий)
ЗАДАЧА 62
Имеются следующие данные о производительности ткачей за час работы:
| Табельные номер ткача | Изготовлено ткани трехстаночниками за 1 час | Табельные номер ткача | Изготовлено ткани четырехстаночниками за 1 час |
| 1 | 13 | 7 | 18 |
| 2 | 14 | 8 | 19 |
| 3 | 15 | 9 | 22 |
| 4 | 17 | 10 | 20 |
| 5 | 16 | 1 | 24 |
| 6 | 15 | 12 | 13 |
Вычислить групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным о производительности труда в двух бригадах.
ЗАДАЧА 63
Имеются следующие данные о производительности труда рабочих:
| Табельный номер рабочего | Произведено продукции в шт. | |
| в дневную смену | в ночную смену | |
| 1 | 5 | 5 |
| 2 | 8 | 6 |
| 3 | 7 | 4 |
| 4 | 4 | 4 |
| 5 | 6 | 6 |
Вычислить групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным о производительности труда в двух сменах.
Дата: 2018-12-21, просмотров: 449.
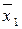 )
)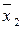 )
)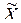 )
) 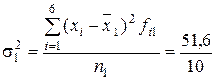 = 5,16
= 5,16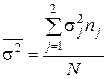 = 4,76
= 4,76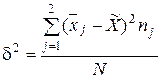 = 4,0
= 4,0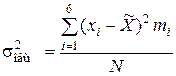 =8,76
=8,76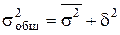 = 4,76 + 4,00 = 8,76
= 4,76 + 4,00 = 8,76