Вариационный ряд по своей конструкции имеет 2 характеристики:
· значения варьирующего признака – варианты x i, i = 1,2,…,m;
· число случаев вариантов: абсолютные – частоты ni (fi), относительные – частности wi (относительные доли частот в общей сумме частот).
Тогда можно сказать, что вариационный ряд – это ранжированный (упорядоченный) в порядке возрастания или убывания ряд статистических частот (частностей).
Вариационные ряды по способу построения бывают дискретные и интервальные.
Дискретный вариационный ряд можно рассматривать как такое преобразование ранжированного ряда, при котором перечисляются отдельные значения признака и указывается их частота.
Если число вариантов велико или признак имеет непрерывную вариацию, то строится интервальный вариационный ряд, в котором отдельные варианты объединяются в интервалы (группы). Существуют следующие виды графического отображения вариационных рядов (рис. 2.1, 2.2):
· полигон для отображения дискретных рядов, когда фиксируются значения ( x i; ni, i = 1,2,…,m);
· гистограмма для отображения интервальных рядов (ki = х(i+1)– хi,
ni(w i));
· кумулята (кумулятивный ряд) – кривая накопленных частот.
Построим по данным задачи 1 соответственно гистограмму, полигон и кумуляту.
Гистограмма изображена на Рис.1.3. Она получена путем выделения двух столбцов таблицы 1.6. Были выделены ячейки в диапазоне С6:D11 (см. Рис.1.2) и выбрана гистограмма в типах предложенных к построению диаграмм.
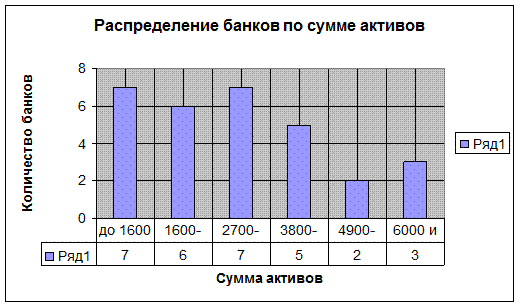 |
Рис. 1.3 Гистограмма
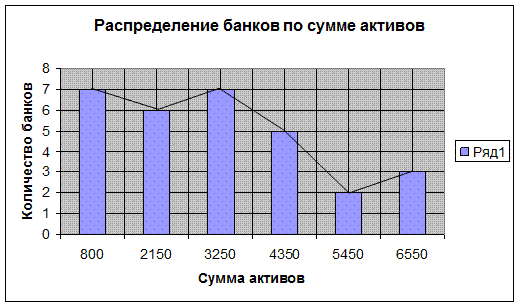 |
Рис. 1.4 Полигон частот
Полигон частот изображен на Рис. 1.4. Мы видим ломанную линию, соединяющую точки соответствующие серединным значениям интервалов группировки и частотам интервалов.
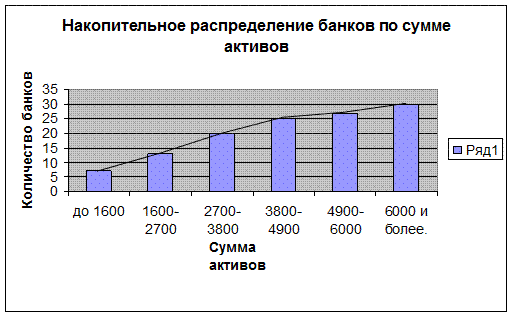
Рис. 1.5 Кумулята
Кумулята изображена на Рис.1.5. Для построения кумуляты необходимо пересчитать столбец таблицы 1.6 «Число банков» в виде накопительной суммы
| Число банков, ед. |
| 7 |
 6 6
|
| 7 |
| 5 |
| 2 |
| 3 |
| Число банков, ед. |
| 7 |
| 7+6 |
| 7+6+7 |
| 7+6+7+5 |
| 7+6+7+5+2 |
| 7+6+7+5+2+3 |
1.5 Контрольные задачи
Тема: построение группировок
ЗАДАЧА 2
Имеются следующие данные о работе 24 заводов одной из отраслей промышленности – Табл.1.9. Провести группировку и построить ряд распределения с 5 равными интервалами. В качестве изучаемого признака взять стоимость основных производственных фондов (аналог Табл.1.6).
Получить таблицы структурной и аналитической группировки (аналог Табл.1.7 и 1.8). Построить гистограмму, полигон частот и кумуляту для изучаемого признака. Сделать выводы.
Таблица 1.9
| Номер п/п | Среднегодовая стоимость основных производственных фондов млн.руб | Среднесписочное число работающих за отчетный период, чел. | Производство продукции за отчетный период в млн.руб. | Выполнение плана в % |
| 1 | 3,0 | 360 | 3,2 | 103,1 |
| 2 | 7,0 | 380 | 9,6 | 120,0 |
| 3 | 2,0 | 220 | 1,5 | 109,5 |
| 4 | 3,9 | 460 | 4,2 | 104,5 |
| 5 | 3,3 | 395 | 6,4 | 104,8 |
| 6 | 2,8 | 280 | 2,8 | 94,3 |
| 7 | 6,5 | 580 | 9,4 | 108,1 |
| 8 | 6,6 | 200 | 11,9 | 125,0 |
| 9 | 2,0 | 270 | 2,5 | 101,4 |
| 10 | 4,7 | 340 | 3,5 | 102,4 |
| 11 | 2,7 | 200 | 2,3 | 108,5 |
| 12 | 3,3 | 250 | 1,3 | 102,1 |
| 13 | 3,0 | 310 | 1,4 | 112,7 |
| 14 | 3,1 | 410 | 3,0 | 92,0 |
| 15 | 3,1 | 635 | 2,5 | 108,0 |
| 16 | 3,5 | 400 | 7,9 | 111,1 |
| 17 | 3,1 | 310 | 3,6 | 96,9 |
| 18 | 5,6 | 450 | 8,0 | 114,1 |
| 19 | 3,5 | 300 | 2,5 | 108,0 |
| 20 | 4,0 | 350 | 2,8 | 107,0 |
| 21 | 1,0 | 330 | 1,6 | 100,7 |
| 22 | 7,0 | 260 | 12,9 | 118,0 |
| 23 | 4,5 | 435 | 5,6 | 111,9 |
| 24 | 4,9 | 505 | 4,4 | 104,7 |
ЗАДАЧА 3
По данным таблицы 1.9 провести группировку и построить ряд распределения с 5 равными интервалами. В качестве изучаемого признака взять среднесписочное число работающих (аналог Табл.1.6). Получить таблицы структурной и аналитической группировки (аналог Табл.1.7 и 1.8). Построить гистограмму, полигон частот и кумуляту для изучаемого признака. Сделать выводы.
ЗАДАЧА 4
По данным таблицы 1.9 провести группировку и построить ряд распределения с 4 равными интервалами. В качестве изучаемого признака взять обьем продукции за отчетный период (аналог Табл.1.6). Получить таблицы структурной и аналитической группировки (аналог Табл.1.7 и 1.8). Построить гистограмму, полигон частот и кумуляту для изучаемого признака. Сделать выводы.
ЗАДАЧА 5
По данным таблицы 1.9 провести группировку и построить ряд распределения заводов по проценту выполнения плана, образовав следующие группы заводов: 1) не выполнившие план
2) выполнившие план от 100% до 104,9% 3) выполнившие план от 105% до 114,9% 4) выполнившие план выше 115%. Получить таблицы структурной и аналитической группировки (аналог Табл.1.7 и 1.8). Построить гистограмму, полигон частот и кумуляту для изучаемого признака. Сделать выводы.
ЗАДАЧА 6
По данным таблицы 1.5 провести группировку и построить ряд распределения с 5 равными интервалами. В качестве изучаемого признака взять численность занятых человек (аналог Табл.1.6). Получить таблицы структурной и аналитической группировки (аналог Табл.1.7 и 1.8). Построить гистограмму, полигон частот и кумуляту для изучаемого признака. Сделать выводы.
ЗАДАЧА 7
По данным таблицы 1.5 провести группировку и построить ряд распределения с 5 равными интервалами. В качестве изучаемого признака взять балансовую прибыль (аналог Табл.1.6). Получить таблицы структурной и аналитической группировки (аналог Табл.1.7 и 1.8). Построить гистограмму, полигон частот и кумуляту для изучаемого признака. Сделать выводы.
ЗАДАЧА 8
По данным таблицы 1.5 провести вторичную группировку произведя укрупнение первоначальных интервалов, выделив по сумме активов баланса мелкие, средние и крупные банки. Получить таблицы структурной и аналитической группировки (аналог Табл.1.7 и 1.8). Построить гистограмму, полигон частот и кумуляту для изучаемого признака. Сделать выводы
ЗАДАЧА 9
Уборка картофеля по хозяйствам Тамбовской области по состоянию на 20 сентября характеризовалась следующими показателями Табл.1.10. Произведите группировку хозяйств области по проценту выполнения плана. Укажите наиболее характерную величину выполнения плана. Постройте гистограмму и кумуляту для изучаемого признака.
Табл.1.10
| Номер хозяйства | Выполнение плана % | Номер хозяйства | Выполнение плана % | Номер хозяйства | Выполнение плана % |
| 1 | 83 | 18 | 12 | 35 | 70 |
| 2 | 67 | 19 | 14 | 36 | 17 |
| 3 | 50 | 20 | 15 | 37 | 18 |
| 4 | 47 | 21 | 26 | 38 | 28 |
| 5 | 41 | 22 | 27 | 39 | 24 |
| 6 | 41 | 23 | 30 | 40 | 33 |
| 7 | 39 | 24 | 27 | 41 | 20 |
| 8 | 33 | 25 | 30 | 42 | 21 |
| 9 | 32 | 26 | 23 | 43 | 18 |
| 10 | 32 | 27 | 16 | 44 | 28 |
| 11 | 30 | 28 | 44 | 45 | 16 |
| 12 | 27 | 29 | 53 | 46 | 31 |
| 13 | 7 | 30 | 6 | 47 | 45 |
| 14 | 10 | 31 | 16 | 48 | 20 |
| 15 | 12 | 32 | 23 | 49 | 23 |
| 16 | 11 | 33 | 17 | 50 | 22 |
| 17 | 11 | 34 | 17 |
|
|
ЗАДАЧА 10
На основании годовых отчетов имеются следующие данные о производстве продукции промышленными предприятиями отрасли Табл.1.11. Произвести группировку предприятий по размеру продукции образовав не более 8 групп. Постройте гистограмму и кумуляту для изучаемого признака.
Таблица 1.11
| Номер предприятия по порядку | Производство продукции, шт. | Номер предприятия по порядку | Производство продукции, шт. | Номер предприятия по порядку | Производство продукции, шт. |
| 1 | 350 | 15 | 356 | 29 | 29 |
| 2 | 175 | 16 | 2700 | 30 | 230 |
| 3 | 990 | 17 | 1900 | 31 | 150 |
| 4 | 3100 | 18 | 130 | 32 | 260 |
| 5 | 2370 | 19 | 1000 | 33 | 305 |
| 6 | 180 | 20 | 220 | 34 | 840 |
| 7 | 1400 | 21 | 270 | 35 | 220 |
| 8 | 250 | 22 | 4850 | 36 | 205 |
| 9 | 1800 | 23 | 5200 | 37 | 305 |
| 10 | 80 | 24 | 90 | 38 | 840 |
| 11 | 75 | 25 | 100 | 39 | 310 |
| 12 | 1253 | 26 | 510 | 40 | 380 |
| 13 | 530 | 27 | 5100 | 41 | 150 |
| 14 | 240 | 28 | 2700 | 42 | 290 |
Статистические показатели
2.1 Методические указания
Абсолютными в статистике называются суммарные обобщающие показатели, характеризующие размеры, объемы, уровни, мощности, темпы и др. изменения величин. Абсолютные показатели являются именованными числами, т.е. измеримы. Существуют: натуральные, стоимостные и условно-натуральные (условное топливо, эталонные лошадиные силы) измерители. Они служат для описания фактического состояния объекта, установления плановых и прогнозных значений. Абсолютные показатели могут быть сравнимы в разные периоды времени (прошлый, настоящий, будущий).
Абсолютные показатели позволяют точно характеризовать объект в данный момент времени, но должны уточняться в динамике (сопоставимые цены, инвестиции с учетом инфляции и т.д.).
Относительные статистические величины – это показатели в виде коэффициентов, характеризующих долю отдельных частей, изучаемой совокупности во всем ее объеме.
Относительные показатели при исследовании экономических явлений и процессов изучаются совместно с абсолютными показателями и обеспечивают сопоставимость сравниваемой и базовой величин.
Относительный показатель динамики (ОПД) представляет собой отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) к уровню этого же процесса или явления в прошлом:
ОПД 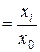 или ОПД
или ОПД 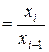 . (2.1)
. (2.1)
Относительный показатель структуры (ОПС) представляет собой отношение структурных частей изучаемого объекта и их целого:
ОПС 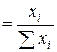 . (2.2)
. (2.2)
Выражается относительный показатель структуры в долях единицы или в процентах. Рассчитанные величины, соответственно называемые долями или удельными весами, показывают, какай долей обладает или какой удельный вес имеет та или иная часть в общем итоге.
Относительный показатель координации (ОПК) представляет собой отношение одной части совокупности к другой части этой же совокупности:
ОПК  . (2.3)
. (2.3)
При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. В результате получают величину, отражающую во сколько раз данная часть больше базисной или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу (иногда – на 100, 1000 и т.д. единиц) базисной структурной части.
Относительный показатель сравнения (ОПСр) представляет собой отношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.):
ОПСр 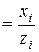 . (2.4)
. (2.4)
Относительный показатель интенсивности (ОПИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды:
ОПИ 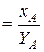 , (2.5)
, (2.5)
где xA – показатель, характеризующий явление А;
YA – показатель, характеризующий среду распространения явления А.
Данный показатель получают сопоставлением уровней двух взаимосвязанных в своем развитии явлений. Поэтому, наиболее часто он представляет собой именованную величину, но может быть выражен и в процентах и т.п.
Обычно ОПИ рассчитывается в тех случаях, когда абсолютная величина оказывается недостаточной для формулировки обоснованных выводов о масштабах явления, его размерах, насыщенности, плотности распространения. Так, например, для определения уровня обеспеченности населения легковыми автомобилями рассчитывается число автомашин, приходящихся на 100 семей, для определения плотности населения рассчитывается число людей, приходящихся на 1 км2.
Разновидностью относительных показателей интенсивности являются относительные показатели уровня экономического развития, характеризующие производство продукции в расчете на душу населения и играющие важную роль в оценке развития экономики государства. Так как объемные показатели производства продукции по своей природе являются интервальными, а показатель численности населения – моментным, в расчетах используют среднюю за период численность населения.
Относительные показатели плана и реализации плана используются для целей планирования и сравнения реально достигнутых результатов с ранее намеченными.
ОПП 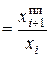 , (2.6)
, (2.6)
где ОПП – относительный показатель плана;
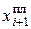 – уровень, планируемый на i+1 период;
– уровень, планируемый на i+1 период;
xi – уровень, достигнутый в i-м периоде.
ОПРП 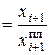 , (2.7)
, (2.7)
где ОПРП – относительный показатель реализации плана;
xi – уровень, достигнутый в (i+1)-м периоде.
ОПП характеризует напряженность плана, т.е. во сколько раз намечаемый объем производства превысит достигнутый уровень или сколько процентов от этого уровня составит. ОПРП отражает фактический объем производства в процентах или коэффициентах по сравнению с плановым уровнем.
Относительные величины выполнения плана и динамики связаны между собой следующими соотношениями:
ОПД = ОПП · ОПРП 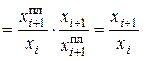 . (2.8)
. (2.8)
Средние величины
Средняя величина является обобщающей характеристикой совокупности однотипных явлений по изучаемому признаку. Средняя величина должна вычисляться с учетом экономического содержания определяемого показателя.
Все виды средних делятся на:
· степенные (аналитические, порядковые) средние (арифметическая, гармоническая, геометрическая, квадратическая);
· структурные (позиционные) средние (мода и медиана) – применяются для изучения структуры рядов распределения.
Средние степенные величины
Средняя степенная (при различной величине k) определяется:
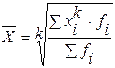 (2.9).
(2.9).
Таблица 2.1 - Виды средних степенных величин
| k | Наименование средней | Формула средней | Когда используется |
| 1 | Средняя арифметическая простая (невзвешенная) | 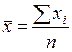 (2.10)
где xi – i-й вариант осредняемого признака ( (2.10)
где xi – i-й вариант осредняемого признака ( 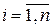 ); n – число вариант ); n – число вариант
| Используется, когда расчет осуществляется по несгруппированным данным |
| 1 | Средняя арифметическая взвешенная | 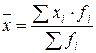 (2.11),
где fi – частота повторяемости i-го варианта (2.11),
где fi – частота повторяемости i-го варианта
| Используется, когда данные представлены в виде рядов распределения или группировок |
| -1 | Средняя гармоническая взвешенная |  (2.12), где (2.12), где 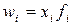 . .
| Используется, когда известны индивидуальные значения признака и веса W за ряд временных интервалов |
| -1 | Средняя гармоническая невзвешенная | 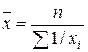 (2.13) (2.13)
| Используется в случае, когда веса равны |
| 0 | Средняя геометрическая невзвешенная | 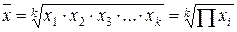 (2.14) (2.14)
| Используется в анализе динамики для определения среднего темпа роста |
| 0 | Средняя геометрическая взвешенная | 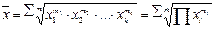 (2.14) (2.14)
| |
| 2 | Средняя квадратическая невзвешенная | 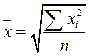 (2.15)
(2.15)
| Используется при расчете показателей вариации |
| 2 | Средняя квадратическая взвешенная | 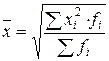 (2.16) (2.16)
|
В статистическом анализе также применяются степенные средние 3-го и более высоких порядков.
Правило мажорантности средних: с ростом показателя степени значения средних возрастают.
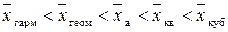 (2.17)
(2.17)
Средняя прогрессивная – средняя для “лучших” значений признака.
Средние структурные величины
В условиях недостаточности средних используют структурные средние величины – моду и медиану.
Медиана (Ме) – это вариант, который находится а середине вариационного ряда. Медиана делит ряд на две равные (по числу наблюдений) части. В ранжированных рядах не сгруппированных данных нахождение медианы сводится к отысканию порядкового номера и значения варианта у этого номера.
Медиана в интервальных вариационных рядах рассчитывается по формуле:
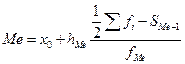 , (2.18)
, (2.18)
где х0 – нижняя граница медианного интервала (накопленная частота которого превышает половину общей суммы частот);
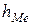 – величина медианного интервала;
– величина медианного интервала;
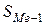 – накопленная частота интервала, предшествующего медианному;
– накопленная частота интервала, предшествующего медианному;
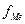 – частота медианного интервала.
– частота медианного интервала.
Также в интервальных вариационных рядах медиана может быть найдена с помощью кумуляты как значение признака, для которого
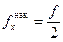 или
или 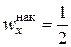 . (2.19)
. (2.19)
Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины: 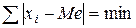 .
.
Модой (Мо) вариационного ряда называется вариант, которому соответствует наибольшая частота.
Для вычисления моды в интервальном ряду сначала находится модальный интервал, имеющий наибольшую частоту (или наибольшую плотность распределения – отношение частоты интервала к его величине ni/hi – в интервальном ряду с неравными интервалами), а значение моды определяется линейной интерполяцией:
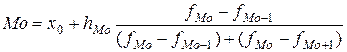 , (2.20)
, (2.20)
где хо – нижняя граница модального интервала;
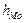 – величина модального интервала;
– величина модального интервала;
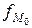 ,
, 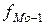 ,
, 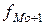 – частота ni (в интервальном ряду с равными интервалами) или плотность распределения ni/hi (в интервальном ряду с неравными интервалами) модального, до и после модального интервала.
– частота ni (в интервальном ряду с равными интервалами) или плотность распределения ni/hi (в интервальном ряду с неравными интервалами) модального, до и после модального интервала.
Мода так же, как и медиана обладает определенной устойчивостью к вариации признака. Если в совокупности первичных признаков нет повторяющихся значений, то для определения моды проводят группировку.
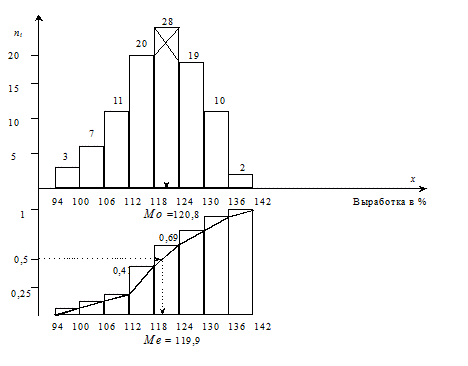 |
Графически отобразить моду по гистограмме можно следующим образом: нужно взять столбец, имеющий наибольшую высоту, и из его левого верхнего угла провести отрезок в угол последующего столбца, а из правого угла – в верхний правый угол предыдущего столбца, абсцисса точки пересечения отрезков и будет соответствовать модальному значению признака в изучаемой совокупности. Медиану приближенно можно определить графически - по кумуляте. Для этого высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения и есть медиана (рисунок 2.1)
Рис. 2.1 Графическое отображение интервального вариационного ряда
В симметричных рядах имеет место следующее соотношение моды, медианы и средней арифметической 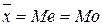 (2.21).
(2.21).
В случае, если 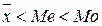 (2.22), имеет место левосторонняя асимметрия ряда.
(2.22), имеет место левосторонняя асимметрия ряда.
В случае, если 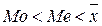 (2.23), имеет место правосторонняя асимметрия ряда.
(2.23), имеет место правосторонняя асимметрия ряда.
Мода и медиана, в отличие от степенных средних, являются конкретными характеристиками ряда. Медиана – характеризует центр, вычисляется проще и не чувствительна к концам интервала. Мода – наиболее вероятное значение в изучаемой совокупности (например, наиболее возможные результаты).
 1 2 3
1 2 3
1 – распределение с левосторонней асимметрией
2 – распределение с правосторонней асимметрией
3 – нормальное (симметричное) распределение
Рис.2.2 Типы асимметрий
2.2 Пример решения задач
Тема: Пересчет абсолютных величин в условные единицы измерения
ЗАДАЧА 11
За отчетный период предприятие произвело следующие виды мыла и моющих средств:
| Виды мыла и моющих средств | Количество, кг |
| Мыло хозяйственное 60%- жирности | 500 |
| Мыло хозяйственное 40%- жирности | 1250 |
| Мыло туалетное 80%-й жирности | 1500 |
| Стиральный порошок 10%- жирности | 2500 |
Требуется определить общее количество выработанной предприятием продукции в условно-натуральных единицах измерения. За условную единицу измерения принимается мыло 40%-й жирности.
Решение: Для определения общего количества продукции, выработанной предприятием, необходимо исчислить коэффициенты перевода. Если условной единицей измерения является мыло 40%-й жирности, то это значение жирности принимается равным единице. Тогда коэффициенты перевода в условное мыло (40%-й жирности) исчисляем так: мыло хозяйственное 60%-й жирности: 60/40=1,5; мыло туалетное 80%-й жирности: 80/40=2,0; стиральный порошок 10%-й жирности: 10/40=0,25. Далее определим количество продукции в условно-натуральных единицах
| Общий объем производства мыла и моющих средств по видам | |||
| Виды мыла и моющих средств | Количество, кг. | Коэффициент перевода | Количество продукции в условно-натуральном исчислении |
| Мыло хозяйственное 60%-й жирности | 500 | 1,5 | 750 |
| Мыло хозяйственное 40%-й жирности | 1250 | 1 | 1250 |
| Мыло туалетное 80%-й жирности | 1500 | 2 | 3000 |
| Стиральный порошок 10%-й жирности | 2500 | 0,25 | 625 |
|
|
|
| Итого - 5625 |
Тема: относительные показатели динамики
ЗАДАЧА 12
Имеются данные о производстве бумаги. Вычислить относительные показатели динамики с переменной и постоянной базой сравнения.
| Год | Произведено бумаги, тыс.т |
| 2007 | 160 |
| 2008 | 235 |
| 2009 | 101 |
| 2010 | 173 |
Решение: Относительные показатель динамики вычисляется по формуле – (2.1)
Расчетные относительные показатели динамики с переменной и постоянной базой сравнения
приведены ниже в таблице:
| Переменная база (цепные показатели) | Постоянная база (базисные показатели) |
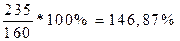 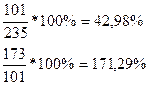
| 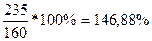 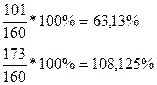
|
Тема: относительный показатель структуры
ЗАДАЧА 13
Имеются следующие данные о составе посевных площадей в агрофирмах и фермерских хозяйствах Тамбовской области на 1 ноября 2010 года (тыс.га)
| Вид культуры | Посевная площадь | |
| Агрофирмы | Фермерские хозяйства | |
| Зерновые | 570,6 | 595,9 |
| Технические | 105,6 | 34,6 |
| Картофель | 27,9 | 17,8 |
| Сахарная свекла | 299,0 | 276,9 |
| ИТОГО | 1003,1 | 925,2 |
Для изучения использования посевных площадей агрофирмами и фермерскими хозяйствами области определить относительные величины структуры и изобразить их графически
Решение: Для расчета относительных величин структуры сопоставим посевные площади, занятые под отдельными культурами с общим итогом (формула 2.2) . определим их удельный вес в процентах:
Зерновые культуры -
В агрофирмах: В фермерских хозяйствах:
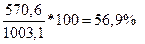
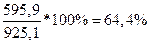
Аналогично исчисляются показатели по остальным видам культур.
В результате расчетов получаем следующие данные о составе посевных площадей в агрофирмах и фермерских хозяйствах Тамбовской области на 1 ноября 2010 года (%)
| Вид культуры | Посевная площадь | |
| Агрофирмы | Фермерские хозяйства | |
| Зерновые | 56,9 | 64,4 |
| Технические | 10,5 | 3,7 |
| Картофель | 2,8 | 1,9 |
| Сахарная свекла | 29,8 | 29,9 |
| ИТОГО | 100,0 | 100,0 |
Из расчетной таблицы видно, что в фермерских хозяйствах на каждые 100 га зерновые культуры занимают на 7,5 га больше, чем в агрофирмах, а удельный вес посевных площадей используемых под картофелем, техническими культурами и сахарной свеклой в агрофирмах выше чем в фермерских хозяйствах. Выявленная специфика получает наглядность в графическом исполнении. Для графического представления относительных величин обычно используются круговые диаграммы. Для этого делается пересчет с коэффициентом 3,6 = 100% / 360 град.
| Вид культуры | Посевная площадь | |
| Агрофирмы | Фермерские хозяйства | |
| Зерновые | 204,8 | 231,9 |
| Технические | 37,9 | 13,5 |
| Картофель | 10,0 | 6,9 |
| Сахарная свекла | 107,3 | 107,7 |
| ИТОГО | 360,0 | 360,0 |
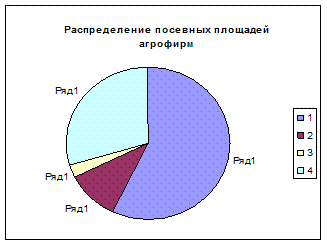

Рис.2.3 Круговые диаграммы
Тема: Относительный показатель структуры и координации
ЗАДАЧА 14
За 2009 год по Тамбовской области получены следующие данные о численности детей родившихся в области, чел.:
Мальчики – 5255 Девочки – 4950
Для определения относительной величины соотношения численности мальчиков и девочек сопоставим между собой исходные данные (приняв за базу сравнения численность родившихся девочек)
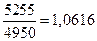
т.е. на каждые 100 девочек рождались 106 мальчиков
ЗАДАЧА 15
Имеются условные данные о внешнеторговом обороте страны, млн. долл. Вычислить относительные показатели структуры и координации.
| Период | I кв.09 г. |
| экспорт | 2693 |
| импорт | 1872 |
Решение: По формулам (2.2) и (2.3) вычислим:
1) 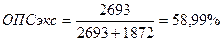
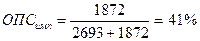
2) 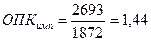 - то есть на каждый млн. рублей импорта приходится 1,44 млн рублей экспорта
- то есть на каждый млн. рублей импорта приходится 1,44 млн рублей экспорта
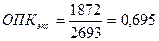 - на каждый млн. рублей экспорта приходится 0,695 рублей импорта
- на каждый млн. рублей экспорта приходится 0,695 рублей импорта
Тема: Относительные показатели плана и реализации плана
ЗАДАЧА 16
Оборот торговой фирмы в 2010 году составил 2,0 млн.рублей. Исходя из рыночных прогнозов руководство фирмы считает реальным в следующем году довести оборот до 2,8 млн.руб. В этом случае относительный показатель плана ОПП (формула 2.6) составит:
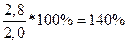
Фактический оборот фирмы в 2011 году составил 2,6 млн.руб. Тогда, ОПРП (формула 2.7) составит:
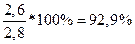 Тогда ОПД (формула 2.8) составит:
Тогда ОПД (формула 2.8) составит:
 или
или 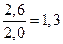
Тема: Средняя арифметическая простая (невзвешенная)
ЗАДАЧА 17
Имеются следующие данные о производстве изделия А за смену:
| Номер рабочего | Выпущено изделий за смену | Номер рабочего | Выпущено изделий за смену |
| 1 | 16,0 | 6 | 17,0 |
| 2 | 17,0 | 7 | 18,0 |
| 3 | 18,0 | 8 | 20,0 |
| 4 | 17,0 | 9 | 21,0 |
| 5 | 16,0 | 10 | 18,0 |
Определим среднюю выработку рабочими данной группы по формуле 2.10:
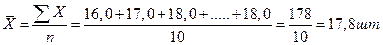
Тема: Расчет средней арифметической взвешенной для дискретного ряда
распределения
ЗАДАЧА 18
Имеются следующие данные о заработной плате рабочих-сдельщиков:
| Месячная заработная плата тыс.руб. варианта x | Число рабочих f | x*f |
| 20 | 2 | 40 |
| 22 | 6 | 132 |
| 25 | 16 | 400 |
| 28 | 20 | 560 |
| 30 | 15 | 450 |
| Итого | 59 | 1582 |
Воспользуемся формулой 2.11:
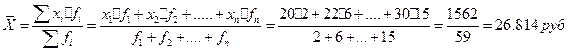
Тема: Расчет средней арифметической взвешенной для интервального ряда
распределения
ЗАДАЧА 19
Имеются следующие данные:
| Группы рабочих по количеству произведенной продукции за смену шт. | Число рабочих f | Середина интервала х | х*f |
| 3-5 | 10 | 4 | 40 |
| 5-7 | 30 | 6 | 180 |
| 7-9 | 40 | 8 | 320 |
| 9-11 | 15 | 10 | 150 |
| 11-13 | 5 | 12 | 60 |
| Итого | 100 |
| 750 |
Исчислим среднюю выработку продукции одним рабочим за смену. В данном случае варианты осредняемого признака представлены не одним числом, а интервалом «от-до». Заменим интервал дискретным числом – серединой интервала. Тогда расчет сведется к формуле 2.11 из предыдущего примера (ЗАДАЧА 18).
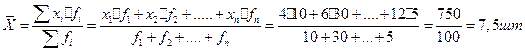
Тема: Средняя геометрическая невзвешенная
ЗАДАЧА 20
По имеющимся данным о темпах роста выпуска продукции определите среднегодовой темп роста за 5 лет.
| Год | Темп роста выпуска продукции, % |
| 2006 | 113 |
| 2007 | 106 |
| 2008 | 98 |
| 2009 | 116 |
| 2010 | 110 |
Решение: при расчете среднегодовых темпов роста используется средняя геометрическая
формула 2.14:
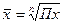 ;
; 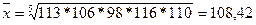
Тема: Средняя гармоническая невзвешенная
ЗАДАЧА 21
Бригада токарей из трех человек должна выточить 460 деталей. Определить, сколько времени (в часах) им потребуется.
| Токарь | Затраты времени токаря на выточку одной детали, мин. |
| Иванов | 8 |
| Петров | 11 |
| Сидоров | 16 |
Решение: Количество деталей в минуту которые изготовляют токари при совместной работе
определяется по формуле 2.13:
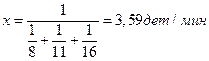
Тогда 460 деталей они изготовят за t= 3,59 *460 = 1652,2 мин = 27,54 ч
Тема: Средняя гармоническая взвешенная
ЗАДАЧА 22
По условным исходным данным о предприятиях, представленным ниже, определите по группе предприятий средние значения:
1) реализованной продукции;
2) производительности труда;
3) заработной платы.
Укажите виды рассчитываемых в каждом случае средних величин.
Дата: 2018-12-21, просмотров: 404.