Для последовательного звена полная группа событий может быть выражена следующим уравнением:
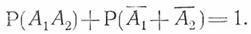
Первое слагаемое уравнения выражает вероятность работоспособности или безотказности звена, второе слагаемое выражает вероятность отказа звена.
Используя теорему умножения независимых событий, получаем следующую формулу для определения вероятности безотказной работы при последовательном соединении:
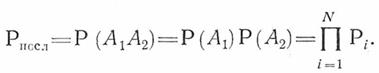
Для вероятности отказа при последовательном соединении из уравнения, представленного выше получаем следующую формулу:
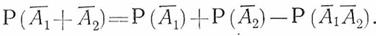
Обозначив 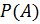 через
через 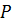 и
и 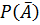 через
через 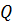 , получаем уравнение для вероятности отказа последовательного звена из двух элементов
, получаем уравнение для вероятности отказа последовательного звена из двух элементов
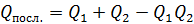
Однако для проведения расчетов удобнее вероятность отказа последовательного звена определять по уравнению 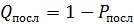 .
.
Формулы параллельного соединения
Полная группа событий для параллельного соединения выражается следующим уравнением:
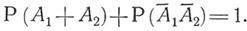
Используя формулу сложения вероятностей совместных событий, получаем следующую формулу вероятности безотказной работы параллельного соединения:
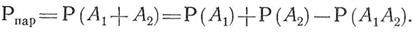
Вероятность отказа параллельного соединения (по формуле умножения вероятностей независимых событий) определяется следующим уравнением:
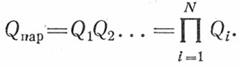
В зависимости от числа элементов в параллельном соединении для равнонадежных элементов вероятность безотказной работы можно определять по следующим формулам:
для двух элементов 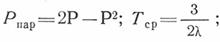
для трех элементов 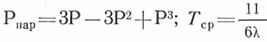
Если структурная схема состоит из 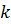 параллельных цепей, а каждая цепь состоит из
параллельных цепей, а каждая цепь состоит из 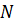 звеньев, то вероятность безотказной работы параллельно-последовательной схемы может быть вычислена по уравнению
звеньев, то вероятность безотказной работы параллельно-последовательной схемы может быть вычислена по уравнению
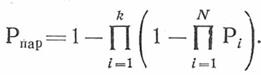
Последовательность решения:
1. Построение структурной схемы.
2. Подбор данных по интенсивностям отказов элементов.
3. Вывод расчетного уравнения для вероятности безотказной работы.
4. Расчет надежности и анализ полученного результата.
Лекция 8
Метод логических схем
При анализе схемной надежности встречаются случаи, когда отсутствуют условия, необходимые для применения расчетного метода структурных схем. Это типично для сложных многофункциональных систем, элементы которых могут иметь несколько видов зависимых отказов.
В логической схеме в отличие от структурной схемы допустимо наличие отдельных звеньев с зависимыми событиями, а также повторение звеньев одинакового содержания. Благодаря этой особенности метод логических схем применим к более широкому кругу задач.
Дата: 2018-12-21, просмотров: 392.