Используется при еще меньшем объеме испытаний. Сущность метода заключается в том, что при проведении испытаний определяется средняя величина, характеризующая надежность ( 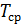 или
или 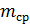 ) и по поправочным коэффициентам, вычисляемым для данной доверительной вероятности и для закона распределения, находятся нижняя и верхняя доверительные границы.
) и по поправочным коэффициентам, вычисляемым для данной доверительной вероятности и для закона распределения, находятся нижняя и верхняя доверительные границы.
Метод максимума правдоподобия
Для числа изделий (или числа опытов) 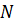 имеем совокупность величины наработки до отказа
имеем совокупность величины наработки до отказа
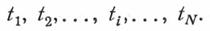
Генеральные характеристики плотности распределения вероятностей неизвестны
( 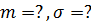 ).
).
Вероятность получения совокупности значений 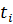 в границах
в границах
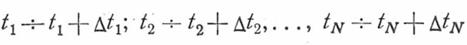
будет равна 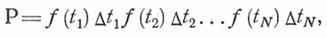
где 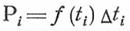 — вероятность того, что величина А примет любые значения в интервале
— вероятность того, что величина А примет любые значения в интервале 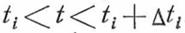 .
.
Если известна аналитическая форма распределения 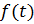 , а неизвестны только параметры
, а неизвестны только параметры 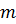 и
и 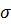 , то можно искать эти параметры исходя из условия получения максимума вероятности
, то можно искать эти параметры исходя из условия получения максимума вероятности 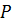 путем подбора оценок
путем подбора оценок 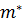 и
и 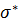 .
.
То есть, при известном 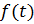 и неизвестных
и неизвестных 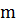 и
и 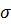 можно подобрать такие значения
можно подобрать такие значения 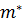 и
и 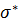 , чтобы вероятность
, чтобы вероятность 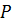 была максимальной.
была максимальной.
Уравнение для вероятности можно переписать следующим образом:
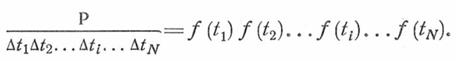
Обозначив это выражение 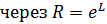 , в результате логарифмирования получаем
, в результате логарифмирования получаем
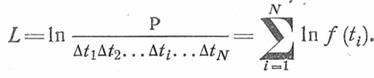
Функция 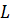 называется функцией правдоподобия.
называется функцией правдоподобия.
Очевидно, при тех значениях 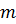 и
и 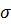 , при которых вероятность
, при которых вероятность 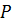 максимальна, будет иметь максимум и функция
максимальна, будет иметь максимум и функция 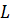 .
.
Оценки параметров 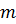 и
и 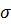 определяют, приравнивая нулю частные производные
определяют, приравнивая нулю частные производные 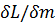 и
и 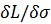 :
:
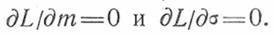
Оценки параметров, полученные в результате решения этих уравнений, называются оценками по методу максимума правдоподобия.
Рассмотрим частный случай усеченной выборки числа изделий 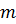 , взятой из совокупности большого числа изделий
, взятой из совокупности большого числа изделий 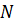 .
.
Для взятой выборки имеем следующие записи по наработке до отказа, расположенные в порядке их возрастания:
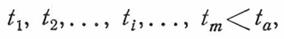
где 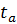 — исследуемый отрезок времени или продолжительность испытаний.
— исследуемый отрезок времени или продолжительность испытаний.
Известно, что все значения от 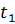 до
до 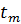 меньше фиксированной величины
меньше фиксированной величины 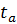 .
.
В случае усеченной выборки с ограничением отрезка времени 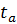 будем иметь следующие уравнения вероятности:
будем иметь следующие уравнения вероятности:
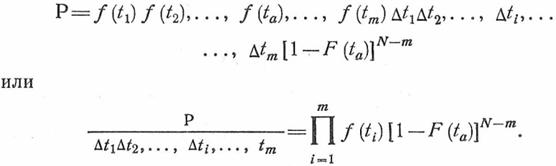
Окончательно получаем выражение для функции правдоподобия
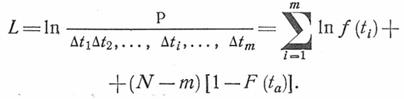
Для случая усеченной выборки при экспоненциальном распределении (искомый параметр Т)
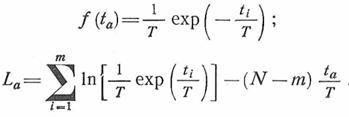
Отсюда находим
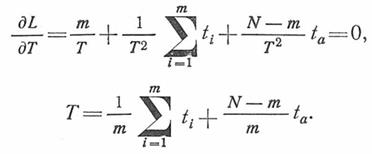
Для случая усеченной выборки числа изделий К при распределении Вейбулла (искомые параметры  и
и 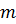 ) в результате решения уравнений частных производных:
) в результате решения уравнений частных производных:
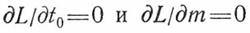
получаются два уравнения с двумя неизвестными
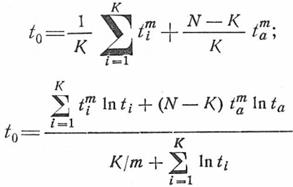
Эту систему уравнений удобнее решать графически (рис. 24), задаваясь рядом значений 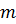 и строя кривые
и строя кривые 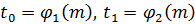 при данных значениях величин
при данных значениях величин 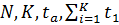 .
.
Точка пересечения этих кривых даст искомые параметры  и
и 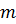 .
.
Дата: 2018-12-21, просмотров: 373.