Этот метод позволяет производить анализ возможности выполнения заданных функций при наличии разнообразных отказов отдельных элементов и звеньев системы.

Анализ схемной надежности методом логических схем выполняется в следующем порядке:

1. формулируются условия безотказной работы системы в целом в зависимости от сочетания возможности появления отказов отдельных элементов или звеньев системы;

2. строится графическая схема условий безотказной работы системы с цепочкой логических связей работоспособности системы и возможных отказов отдельных звеньев;

3. составляются алгебраические уравнения событий безотказной работы и расчетные уравнения вероятностей с использованием методов алгебры логики;

4. производится подбор и подготовка количественных характеристик надежности элементов, входящих в систему;

5. производится количественный расчет вероятности безотказной работы системы в целом и отдельных ее частей.

Прежде чем перейти к практическому применению данного метода рассмотрим основные положения алгебры логики (алгебры Буля).

Положения алгебры логики (алгебры Буля)

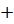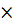В алгебре Буля есть две основные операции – логическое сложение и логическое умножение – « » и « ») – соответствуют двум словам «или» и «и».

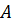 - основное событие (в нашем случае событие безотказности);

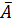 - противоположное событие (отказ);

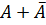 - полная группа событий, , .

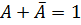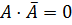Логическое сложение выражает событие, когда при котором достоверно хотя бы одно из событий ( ).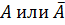

Логическое умножение выражает событие, когда при котором достоверно достоверны оба события ( ).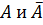

Можно рассмотреть в качестве примера небольшую часть блока питания высотного запуска.

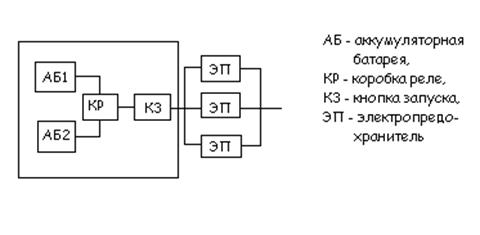
Для простой схемы можно совместить формирование условий безотказной работы с графической схемой ее безотказности.

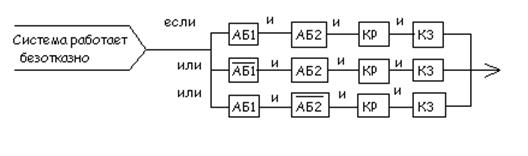
Вслед за графической схемой безотказности необходимо составить уравнение события безотказной работы, где «и» заменяются знаком умножения событий, а «или» - сложением.

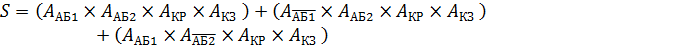
Уравнение вероятности безотказной работы системы может быть получено заменой событий безотказной работы элементов на вероятности их безотказной работы, а событий отказа на вероятности отказа:

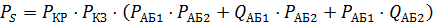
Свойства элементарных логических операций:

1. свойство ассоциативности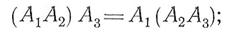

2. свойство коммутативности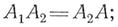

3. свойство дистрибутивности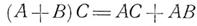

4. свойство идемпотентности:

Для логического умножения справедливо .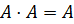

Для логического сложения справедливо .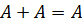

При этом, отметим, что знак «-» нигде не применяется.

Расчет надежности сложных многофункциональных систем (схемно-функциональный метод или метод матриц)