Если обозначить через 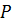 вероятность появления отказа в каждом из испытаний (
вероятность появления отказа в каждом из испытаний ( 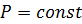 ),
), 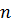 — число испытаний,
— число испытаний, 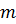 - возможное число появления отказов при
- возможное число появления отказов при 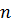 испытаний, то вероятности возможных значений
испытаний, то вероятности возможных значений 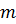 , т.е. вероятности возможных значений рассматриваемой случайной величины
, т.е. вероятности возможных значений рассматриваемой случайной величины 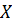 , определяются по формуле Бернулли:
, определяются по формуле Бернулли:
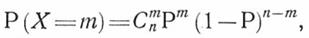
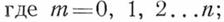
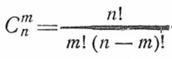 - число всех возможных сочетании, которое можно образовать из
- число всех возможных сочетании, которое можно образовать из 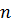 испытаний, собирая в каждом из них по
испытаний, собирая в каждом из них по 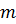 отказов.
отказов.
Распределение дискретной случайной величины, определяемое данной формулой, называется биноминальным распределением.
В качестве примеров практического применения биномиального закона можно указать:
1. статический контроль качества выборки изделия, составляющей не более 10% от объема партии;
2. определение количества отказов невосстанавливаемых изделий в течение заданного времени при их испытаниях.
В обоих случаях количество бракованных изделий или количество отказов подчиняется биномиальному закону распределения.
Биноминальное распределение так же может использоваться для определения количества отказов неремонтируемых изделий в течении заданного времени испытаний при достаточно большой вероятности отказа ( 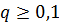 ).
).
При 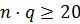 может быть заменено нормальным законом распределения.
может быть заменено нормальным законом распределения.
Распределение Пуассона
Распределение Пуассона, иногда, так же, как и биномиальное распределение, распространяется на те случаи, когда случайная величина принимает целые и положительные значения.
Физический смысл распределения Пуассона такой же, как и биномиального, т.е. оно определяет вероятность появления в малых выборках различных значений случайной величины 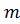 (например, отказов).
(например, отказов).
Эта вероятность находится по формуле: 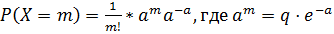 ;
;
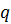 – вероятность отказа в одном испытании;
– вероятность отказа в одном испытании; 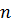 —количество изделий в выборке;
—количество изделий в выборке;
Сущность распределения Пуассона может быть показана геометрически.
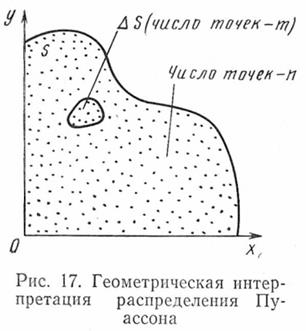
| Допустим в координатной плоскости 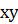 выделена фиксированная площадь выделена фиксированная площадь 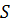 , в которой случайным образом распределено определенное число точек , в которой случайным образом распределено определенное число точек 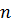 .
Необходимо знать, с какой вероятностью можно ожидать, что в элементарную площадку .
Необходимо знать, с какой вероятностью можно ожидать, что в элементарную площадку 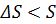 из общего числа точек попадает заданное число точек из общего числа точек попадает заданное число точек 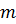 . .
|
При этом, должны соблюдаются следующие условия:
1. точки распределены на площади 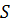 с одинаковой плотностью
с одинаковой плотностью 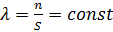 , т.е. имеет место простейший поток точек (свойство стационарности);
, т.е. имеет место простейший поток точек (свойство стационарности);
2. распределение точек в плоскости независимое, т.е. попадания того или иного числа точек в неперекрывающиеся участки площади независимы;
3. 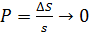 , т.е. вероятность попадания двух или более точек на элементарную площадку
, т.е. вероятность попадания двух или более точек на элементарную площадку 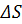 пренебрежимо мала по сравнению с попаданием одной точки (свойство ординарности).
пренебрежимо мала по сравнению с попаданием одной точки (свойство ординарности).
Т.е., для 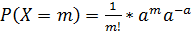 , в рассмотренной геометрической интерпретации закона Пуассона величина
, в рассмотренной геометрической интерпретации закона Пуассона величина 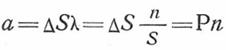 .
.
Распределение Пуассона можно использовать:
1. как заменитель биномиального распределения в тех случаях, когда действует биномиальный закон, но вероятность 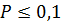 ;
;
2. при выполнении ряда расчетов по надежности и при испытаниях ремонтируемых изделий, для которых распределение Пуассона имеет самостоятельное значение.
В частности, для ремонтируемых изделий при установившихся режимах работы случайное число отказов распределено по закону Пуассона. В этом случае возможность применения закона Пуассона не зависит от величины вероятности 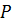 .
.
Для того чтобы доказать правильность предположения о наличии пуассоновского распределения случайных величин на практике вычисляют 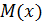 и
и 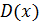 . И, если их значения близки, то это подтверждает правильность предположения о наличии распределения Пуассона.
. И, если их значения близки, то это подтверждает правильность предположения о наличии распределения Пуассона.
Заметим, что распределение Пуассона при 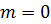 трансформируется в экспоненциальное распределение.
трансформируется в экспоненциальное распределение.
Дата: 2018-12-21, просмотров: 403.