Тема 3.1. Множества и отношения

Элементы и множества. Задание множеств. Операции над множествами. Свойства операций над множествами. Отношения. Свойства отношений. Основные понятия теории графов.

[1] Глава 5, стр. 227-244;

[2] Глава 1, стр. 12-20; Глава 2 стр. 31-50.

Множества.

Под множеством будем понимать совокупность (систему) каких-либо объектов произвольной природы, обладающих некоторым общим признаком.

Обозначение: А, B, C, D, …

Объекты, образующие множество, называются элементами множества и обозначаются соответствующими малыми буквами. Например, множество людей, множество городов России, множество целых чисел.

Некоторые множества имеют общепринятое обозначение:

N – множество натуральных чисел.

Z – множество целых чисел.

I – множество иррациональных чисел.

Q – множество рациональных чисел.

R – множество действительных чисел.

С – множество комплексных чисел.

Способы задания множеств:

- перечислением всех входящих в него объектов;

- описанием свойств, которыми должны обладать элементы множества. Такой способ называется аналитическим.

Например, множество M арабских цифр можно задать двояко: перечислением M={0,1,2,…,9} или посредством свойства M={x| х – арабская цифра}.

Множество, не содержащее ни одного элемента, называют пустым и обозначают Æ.

Количество элементов множества А называется мощностью множества и часто обозначают .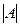

Пример 26. Мощность множества арабских цифр 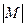=10.

Если число элементов множества ограничено, то множество называют конечным, в противном случае – бесконечным.

Любую часть А (даже целую)множества В, выбранную по определённому признаку, называют подмножеством. Записывают

.

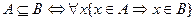Пример 27. Справедливы следующие включения: NÍZ, ZÍQ, QÍR, RÍC,

{1; 4}Í{1;4;5;6;8}.

Операции над множествами

Рассмотрим исполнение отдельных операций над подмножествами A, B, C множества U.

а) АÈВ (объединение) – множество, состоящее из всех элементов множеств А и В, записанных в порядке возрастания и без повтора.

б) АÇВ (пересечение) – множество, составленное из общих (одинаковых) элементов множеств А и В.

в) А \ В (разность) – множество, составленное лишь из тех элементов множества А, которые не встречаются во множестве В.

г) 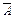 (дополнение) – множество элементов универсального множества U, которых нет в множестве А. За универсальное множество удобно взять множество целых чисел Z.

д) АDВ (симметрическая разность) – множество, состоящее из элементов множеств А и В, не включая их общие (одинаковые) элементы

Пример №28. Дано множество U={1;2;3;4;5;6;7;8;9;10} и множества А={2;3;4;5}, В={1;4;5;6;8} и С={4;6;7;9;10}. Записать множества:

1) АÈВ      2) АÇВ      3) АÈ(ВÇС)         4) 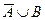   5) В\С        6)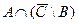

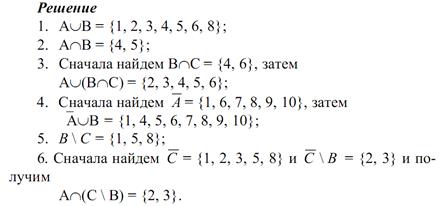
Вопросы для повторения

1. Дайте определение множества и приведите пример.

2. Какие способы задания множеств Вы знаете?

3. Перечислите основные числовые множества и их обозначения.

4. Что такое мощность множества?

5. Что такое подмножество? Приведите пример.

Раздел 4. Численные методы