Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения. Однородные дифференциальные уравнения первого порядка. Линейные уравнения второго порядка с постоянными коэффициентами.

[1] Глава 4, стр. 206-226;

[2] Глава 9, стр. 206-220;

[3] Глава 9, стр. 282-287;

[4] Глава 15, стр. 243-256;

[5] Часть 2, Глава 4, стр. 117-166.

Определение дифференциального уравнения, его порядок и решение

Дифференциальным уравнением называют отношение, связывающее независимую переменную х, искомую функцию y=f(x) и её производные.

Если искомая функция есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным.

Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком данного уравнения.

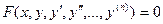
- уравнение n-го порядка.

Всякая функция y=f(x), которая, будучи подставлена в дифференциальное уравнение, обращает его в тождество, называется решением этого уравнения.

Например, докажем, что функция 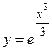 является решением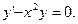

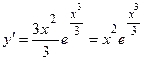            , т.е.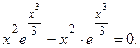

Следовательно, функция 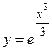 является решением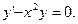

Дифференциальное уравнение первого порядка, общее решение и начальные условия

Дифференциальное уравнение первого порядка имеет общий вид

F(x,y,y¢)=0

или (если это уравнение можно разрешить относительно y’) вид

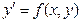.                                           (7)

Пусть y= j(x) – решение уравнения (9.1), тогда кривая определяемая уравнение y= j(x), называется интегральной кривой дифференциального уравнения (1).

Решение уравнения (1), содержащее произвольную постоянную С, т.е. имеющее вид

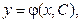
называется общим решением этого уравнения.

В неявной форме

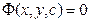 или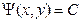

называется общим интегралом дифференциального уравнения первого порядка (7).

Решить или проинтегрировать дифференциальное уравнение, значит найти его общее решение в той или иной форме.

Решение, которое получается из общего решения при некотором фиксированном значении произвольной постоянной C, называется частным решением.

Теорема Коши о существовании решения дифференциального уравнения первого порядка.

Если в уравнении (1) функция f( x, y) и её частная производная f_у’ ( x, y) непрерывны в некоторой области D на плоскости хОу, содержащей некоторую точку (х₀,у₀), то существует единственное решение этого уравнения 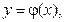 удовлетворяющее условию при х=х₀, у=у₀.

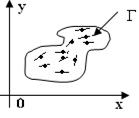Геометрический смысл этой теоремы, состоит в том, что существует и при этом единственная функция 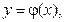график которой проходит через точку(х₀,у₀).

Условие, что при х=х₀ функция у должна равняться заданному значению у₀, называется начальным условием.

Начальное условие дает возможность выделить из общего решения (2) частное решение.