Абсолютная и относительная погрешности. Округление чисел. Погрешности простейших арифметических действий. Численное решение уравнений с одной переменной.
[1] Глава 6, стр. 245-252;
[2] Глава 2, стр. 39-41;
[3] Глава 1, стр.26-39;
[4] Глава 1-2, стр. 10-24.
Основные понятия.
Модуль (абсолютная величина) разности между точным числом х и его приближенным значением а называется абсолютной погрешностью приближенного значения числа х и обозначается через α, т. е. |х – а| = α.
Число а называется приближенным значением точного числа х с точностью до Dа, если абсолютная погрешность приближенного значения а не превышает Dа, т. е.
|х - а| ≤ Dа.
Число Dа называется границей абсолютной погрешности приближенного числа а.
Пример №29. Даны приближенные значения числа х= 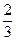 : а1 = 0,6; а2 = 0,66; а3= 0,67. Какое из этих приближений является лучшим?
: а1 = 0,6; а2 = 0,66; а3= 0,67. Какое из этих приближений является лучшим?
r Найдем абсолютную погрешность каждого приближенного значения.
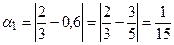 ,
,
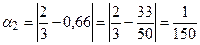 ,
,
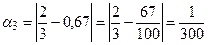 .p
.p
Относительной погрешностью 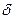 приближенного значения а числа х называется отношение абсолютной погрешности
приближенного значения а числа х называется отношение абсолютной погрешности  этого приближения к числу а, т.е.
этого приближения к числу а, т.е. 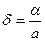 .
.
Число 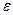 называется границей относительной погрешности, если
называется границей относительной погрешности, если 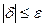 .
.
Действия над приближенными числами.
1. Сложение.
Граница абсолютной погрешности суммы (разности) приближенных значений чисел равна сумме границ абсолютных погрешностей этих чисел: 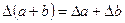 , где а и b – приближенные значения чисел,
, где а и b – приближенные значения чисел, 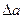 и
и  - границы абсолютных погрешностей соответствующих приближений.
- границы абсолютных погрешностей соответствующих приближений.
Граница относительной погрешности суммы вычисляется по формуле
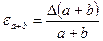 .
.
Пример №30. Электрическая цепь состоит из трёх последовательно соединённых проводников с сопротивлениями r1=6,8±0,05 (Ом), r2=4,3±0,05 (Ом), r3=3,575±0,0005 (Ом). Вычислите общее сопротивление цепи R. Найдите границы абсолютной DR и относительной eR погрешностей.
r R = 6,8+4,3+3,575=14,675; 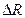 =0,05+0,05+0,0005=0,1005.
=0,05+0,05+0,0005=0,1005.
Граница абсолютной погрешности заключена в пределах 0,05<0,1005<0,5.
Граница относительной погрешности
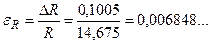
В процентах 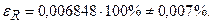 p
p
2. Вычитание.
Граница абсолютной погрешности разности двух приближенных значений чисел равна сумме границ абсолютных погрешностей этих чисел: 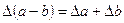 .
.
Граница относительной погрешности разности вычисляется по формуле
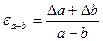 .
.
Пример №31. Вычислить разность двух приближенных значений чисел 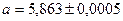 и
и 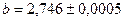 . Найти
. Найти 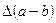 и
и 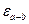 .
.
r Вычислим границу абсолютной погрешности разности a-b:
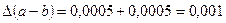 .
.
В приближенном значении разности цифра в разряде тысячных не может быть верной, так как 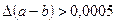 , следовательно,
, следовательно, 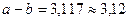 . Абсолютная погрешность разности 0,001. Находим относительную погрешность разности:
. Абсолютная погрешность разности 0,001. Находим относительную погрешность разности: 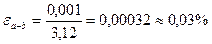 .p
.p
3. Умножение и деление.
Формулы для оценки границ абсолютной погрешности произведения (частного) сложны, поэтому сначала находят относительную погрешность произведения (частного), а затем границу абсолютной погрешности произведения (частного).
Формулы для границ абсолютной и относительной полгрешности приведены в таблице 2.
Таблица 2.
| Функция | Граница абсолютной погрешности | Граница относительной погрешности |
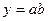
| 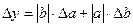
| 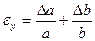
|
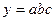
| 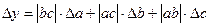
| 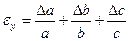
|
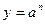
| 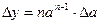
| 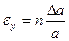
|
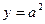
| 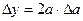
| 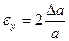
|
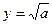
| 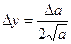
| 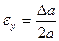
|
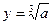
| 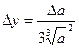
| 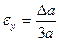
|
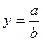
| 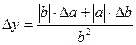
| 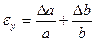
|
Пример №32. Найдите границы абсолютной и относительной погрешности вычисления площади жестяной пластины прямоугольной формы с измерениями а=12±0,05(см) и b=10±0,05(см)..
r Площадь прямоугольника S=a×b, следовательно, граница абсолютной погрешности вычисления площади
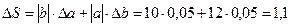 (см)
(см)
Граница относительной погрешности
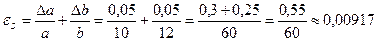 p
p
Пример №33. Вычислите силу тока I (A) в однородном участке цепи с напряжением U=120±0,5(В) при постоянном сопротивлении участка R=40±0,1(Ом). Найдите границы абсолютной DI и относительной eI погрешности вычисления.
r Имеем 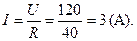
Граница абсолютной погрешности
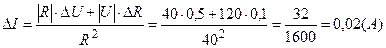
Границу относительной погрешности вычислим по формуле
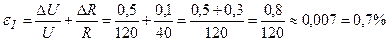 p
p
Вопросы для повторения
1. Что называется абсолютной погрешностью приближенного числа?
2. Что называется границей абсолютной погрешности?
3. Что называется относительной погрешностью приближенного числа?
4. Что называется границей относительной погрешности приближенного числа?
5. Что называется округлением десятичной дроби?
6. Что называется погрешностью округления?
7. Как производится округление с недостатком?
8. Как производится округление с избытком?
9. Как вычисляется граница абсолютной и относительной погрешности суммы приближенных значений чисел?
10. Как вычисляется граница абсолютной погрешности разности двух приближенных значений чисел?
11. Как вычисляется граница относительной погрешности разности приближенных значений чисел?
12. Как вычисляется граница абсолютной и относительной погрешности произведения и частного приближенных значений чисел?
13. Как вычисляется граница абсолютной и относительной погрешности степени приближенного значения числа?
14. Как вычисляется граница абсолютной и относительной погрешности квадратного и кубического корней из приближенных значений чисел?
Дата: 2018-12-21, просмотров: 492.