Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Теорема. Вероятность суммы конечного числа несовместимых событий равна сумме их вероятностей:

.

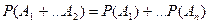Пример №36. Пусть вероятность того, что в магазине очередной будет про­дана пара мужской обуви 44-го размера, равна 0,12, 45-го — 0,04, 46-го или большего — 0,01. Найти вероятность того, что очередной будет продана пара мужской обуви не менее 44-го размера.

r Искомое событие произойдет, если будет продана пара обуви 44-го размера, или 45-го, или не менее 46-го (событие С), т. е. искомое событие есть сумма этих трех событий. События А, В и С несовместимы. Поэтому, применяя теорему сложения вероятностей, получим: Р( D) =  Р (А + В+ С) = Р (А) + Р (В) + Р (С) = 0,12 + 0,04 + 0,01 = 0,17. p

Следствие 1. Сумма вероятностей событий, образующих полную систему, равна единице.

Следствие 2. Вероятность события, противоположного со­бытию А, равна разности между единицей и вероятностью собы­тия А, т.е.

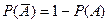
Пример №37. В условиях задачи №3 найти вероятность того, что очередной будет продана пара обуви меньше 44-го размера:

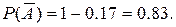
Теорема (сложения вероятностей совместных событий). Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления

P(A+B)=P(A)+P(B)-P(AB).

Пример №38. Игральная кость брошена один раз. Какова вероятность выпадения «двойки» или четного числа?

r События совместимы. Поэтому p=1/6+3/6-1/6=3/6. p

Теорема умножения вероятностей.

Вероятность события А, найденная в предпо­ложении, что событие В наступило, называется условной вероятностью события А относительно события В.

Обозначать ее будем символом Р_В(А).

Теорема (умножения вероятностей). Вероят­ность произведения событий А и В равна произведению вероятности одного из них на условную вероятность другого относительно взятого первым, т. е.

Р (АВ) = Р (А) • Р_А (В) или Р ( AB)= Р (В) • Р_В (А).

Пример №39. Среди 25 электрических лампочек четыре нестандартные. Найти вероятность того, что две взятые одновременно лампочки окажутся не­стандартными.

r Искомое событие состоит в том, что нестандартными будут и первая (событие А) и вторая (событие В) лампочки. Но Р(А) = 4/25, а Р_А (В) = 3/24, так как при наступлении собы­тия А общее число лампочек и число нестандартных среди них по сравнению с первоначальным уменьшится на одну.

Таким образом, Р (АВ) = 4/25*3/24=0,02. p

События А и В называются независимыми, ес­ли вероятность одного из них не изменяется при наступлении другого. В противном случае события А и В называются зависимыми.

Теорема. Вероятность произведения двух независимых событий равна произведению их вероятностей:

 

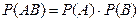
Пример №40. Считая вероятность безотказной работы станка в течение смены равной 0,9, найти вероятность безотказной работы двух станков в течение смены.

r Считая события А и В, состоящие в безотказной работе в те­чение смены соответственно первого и второго станков, независимыми и применяя к ним теорему умножения вероятностей получим: Р (АВ) = 0,9 • 0,9 =0,81. p

Теорема. Вероятность произведения конечного числа зависимых событий равна произведению их условных вероятностей относительно произве­дения предшествующих каждому из них событий, т. е.

Р (АВС...К L) = Р(А) • Р_А (В) • P_AB (С) ... P_{ABC… K} ( L).

Пример №41. В партии из 25 деталей 5 деталей содержат брак. Рабочий случайным образом извлекает три детали. Какова вероятность, что ему попадутся:

а) три стандартные детали,

б) хотя бы одна стандартная деталь?

r а) Обозначим события: A – рабочий извлек первую стандартную деталь, В – рабочий извлек вторую стандартную деталь, С – рабочий извлек третью деталь без брака. Тогда вероятность того, что  рабочий извлечёт все три стандартные детали P= 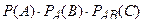. Т.е.

P = .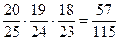

б) Пусть D – рабочему попадется хотя бы одна стандартная деталь. Противоположное событие – что не извлечёт ни одной стандартной детали. P( D)=1- 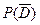, то есть P( D) = 1- 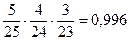.p

Пример №42. Студент знает 15 вопросов из 30 в первом разделе курса и 25 из 40 вопросов второго раздела этого курса. В билете по одному вопросу из каждого раздела. Найти вероятность того, что студент:

1) знает ответы на оба вопроса;

2) не знает ответов на оба вопроса;

3) знает ответ только на один вопрос в билете.

r Обозначим общее число вопросов первого раздела курса n₁ =30, а количество выученных вопросов этого раздела (т.е. благоприятствующих хорошему ответу) т₁ = 15.

Общее число вопросов второго раздела курса n₂= 40, а количество выученных вопросов этого раздела (т.е. благоприятствующих хорошему ответу) т₂ = 25.

Далее введём обозначения следующих событий:

А - событие, состоящее в том, что студент знает ответ на вопрос, случайным образом предложенный ему из первого раздела курса;

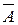 - противоположное событие, состоит в том, что студент не знает ответ на вопрос, случайным образом предложенный ему из первого раздела курса.

Событие В состоит в том, что студент знает ответ на вопрос, случайным образом предложенный ему из второго раздела курса;

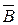 – противоположное событие, состоит в том, что студент не знает ответ на вопрос, случайным образом предложенный ему из второго раздела курса.

Вероятности событий А и В найдём, пользуясь классическим определением вероятности:

.

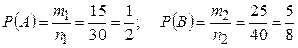Вероятности противоположных событи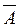й  и 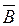 определим, исходя из соотношения между вероятностями противоположных событий:

1) Для нахождения ответа на первый пункт введем обозначение еще одного события С – студент знает ответы на оба случайным образом предложенных ему вопроса из первого и второго разделов курса.

Опираясь на понятие произведения двух событий, видим, что .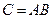

Для нахождения вероятности события С применим теорему умножения вероятностей независимых событий:

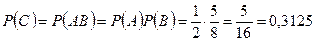
2) Для решения второго пункта задачи введем еще одно обозначение события: событие D состоит в том, что студент не знает ответы на оба случайным образом предложенных ему вопроса из первого и второго разделов.

Опираясь на понятие произведения двух событий, получаем, что .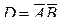

Для нахождения вероятности события D применим еще раз теорему умножения вероятностей независимых событий:

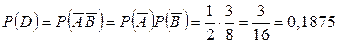
3) Для решения третьего пункта введем ещё одно обозначение события: событие Е состоит в том, что студент знает ответ только на один из двух случайным образом предложенных ему вопросов из первого или второго разделов курса, причем безразлично на какой именно—первый или второй.

Это сложное событие может проявиться в виде двух несовместных вариантов: или студент знает ответ на вопрос из первого раздела и не знает ответ на вопрос из второго раздела, т.е. ;  или же студент не знает ответ на вопрос из первого раздела и знает ответ на вопрос из второго раздела, т.е. .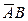

Таким образом, событие .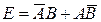

Для нахождения вероятности этого события применим теорему сложения вероятностей несовместимых событий

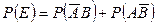
Применяя к каждому из слагаемых теорему умножения вероятностей, получаем:

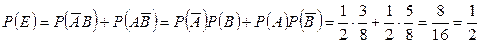.p

Формула полной вероятности.

Пусть событие А может произойти лишь при условии появления одного из n попарно несовместных событий 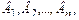образующих полную группу событий. События  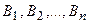 будем называть гипотезами для события А. Тогда вероятность события А

 

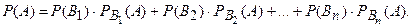
Пример №43. Магазин получил две равные по количеству партии обуви в одинаковых упаковках. Известно, что в среднем 8% обуви в первой партии и 14% во второй партии имеют определённые дефекты отделки верха. Какова вероятность того, что взятая наугад в магазине пара обуви будет иметь дефект отделки верха?

r Эта задача решается с применением формулы полной вероятности.

Введём обозначение событий. Пусть:

- событие А состоит в том, что наугад выбранная пара обуви имеет дефект отделки верха;      

- гипотеза H ₁ состоит в том, что наугад выбранная пара обуви взята из первой партии;

- гипотеза H₂ состоит в том, что наугад выбранная пара обуви взята из второй партии.

Вероятность события А найдём, пользуясь формулой полной вероятности:

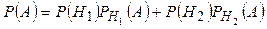
Так как по объёму обе партии одинаковые, то вероятности Р(H₁) и Р(H₂) равны между собой и Р(H₁)=Р(H₂)=0,5.

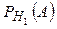 - условная вероятность того, что наугад взятая пара обуви из первой партии имеет дефект отделки верха. По условию задачи .

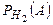- условная вероятность того, что наугад взятая пара обуви из второй партии имеет дефект отделки верха.

По условию задачи .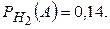

Подставляем все вероятности в формулу полной вероятности:

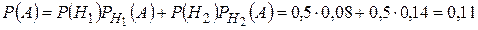.p

 

Вопросы для повторения

1. Сформулируйте классическое определение вероятности. В чем ограниченность этого определения?

2. В чем различие между вероятностью и относительной частотой?

3. Дайте определение суммы событий. Приведите примеры: суммы двух несовместных событий; суммы двух совместных событий.

4. Сформулируйте и докажите теорему о сложении вероятностей несовместных событий.

5. Дайте определение произведения событий. Приведите примеры: произведения двух независимых событий; произведения двух зависимых событий.

6. Что такое условная вероятность?

7. Сформулируйте теорему об умножении вероятностей для двух событий (общий случай). Какую форму принимает эта теорема в случае, когда события независимы?