Производной n -го порядка называется производная от производной ( n -1)-го порядка.
Обозначение производных: f ¢¢- второго порядка (или вторая производная), f ¢¢¢ - третьего порядка (или третья производная).
Для обозначения производных более высокого порядка используются арабские цифры в скобках или римские цифры, например, f(4)(x), …, f(n)(x) или f IV и т.д.
Пример №10 Найдите производную 3-го порядка функции f(x)=5х4–3х3+2х–2 в точке х=2.
rНаходим вначале первую производную:
f ¢(x) = 20х3 – 9х2 +2,
затем вторую от первой производной: (f ¢(x))¢ = f ¢¢(x)=( 20х3 – 9х2 +2)¢=60х2 – 18х.
Третья производная f ¢¢¢(x)=(f ¢¢(x))¢=(60х2-18х)¢=60×2х-18=120х-18.
Вычислим значение 3-й производной в точке х=2: f¢¢¢(2)=120×2 – 18=240 -18=222. p
Производная сложной функции.
Пусть функция g(x) имеет производную в точке x, а функция f(z) имеет производную в точке z = g(x). Тогда сложная функция F(x) = f(g(x)) имеет в точке x производную F ¢ (x) = f ¢ (z) g¢ (x).
Пример №11 Вычислите производную функции:
а) f(x)=sin2x; б) f(x)=sinx2; в) f(x)=lncosx; г) f(x)=cos(lnx); д) f(x)=(x3-3)6; e) f(x)= 
r a) f ¢(x)=2sinx×(sinx)¢=2sinx×cosx=sin2x;
б) f ¢(x)=cosx2×(x2)¢=cosx2×2x=2x×cosx2;
в) f ¢(x)= 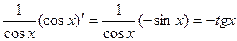 ;
;
г) f ¢(x)=-sin(lnx)×(lnx)¢=-sin(lnx)× 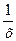 ;
;
д) f ¢(x)=6(x3-3)5×(x3-3)¢=6(x3-3)5×3x2=18x2(x3-3)5;
е) f ¢(x)= 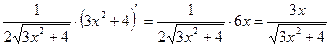 .p
.p
Производная обратной тригонометрической функции
Формулы производных обратных тригонометрических сложных функций
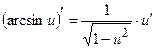
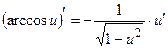
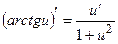
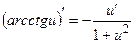
Пример №12. Вычислите производную обратной тригонометрической функции 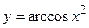 .
.
rЗадана сложная обратная тригонометрическая функция, где u=х2. Используем формулу: 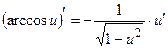 .
.
у¢=(arccosx2)¢= 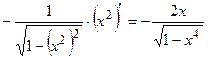 . p
. p
Неопределенный интеграл. Методы вычисления
Функция F( x) называется первообразной для функции f( x), если 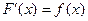 или
или 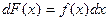 .
.
Любая непрерывная функция f(x) имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым.
Совокупность F(x)+С всех первообразных для функции f(x) называется неопределенным интегралом от этой функции и обозначается:
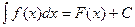 .
.
Основные свойства неопределенного интеграла:
1. 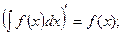 2.
2. 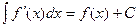 ;
;
3. 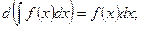 4.
4. 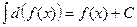 ;
;
5. 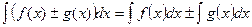 ; 6.
; 6. 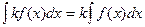 .
.
Непосредственное интегрирование
Непосредственное интегрирование предполагает использование при нахождении неопределенных интегралов таблицы интегралов
Таблица неопределенных интегралов
Основные формулы интегрирования Дополнительные формулы интегрирования:
1) 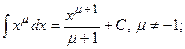 11)
11) 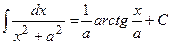 ;
;
2) 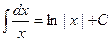 ; 12)
; 12) 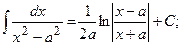
3) 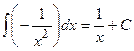 ; 13)
; 13) 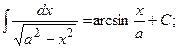
4) 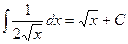 ; 14)
; 14) 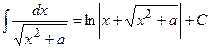 ;
;
5) 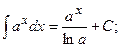 15)
15) 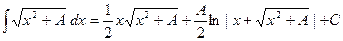 ;
;
6) 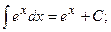 16)
16) 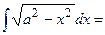
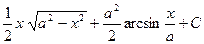 ;
;
7) 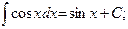 17)
17) 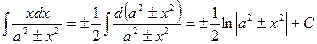 ;
;
8) 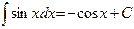 ; 18)
; 18) 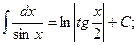
9) 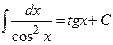 ; 19)
; 19) 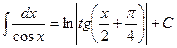 .
.
10) 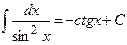 ;
;
Рассмотрим нахождение интегралов непосредственным методом.
Пример №13: Найти неопределенный интеграл:
а) 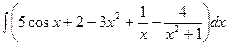 ; б)
; б) 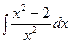 ; в)
; в) 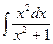 .
.
r а) 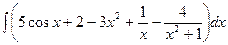 =
= 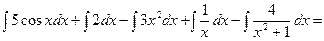
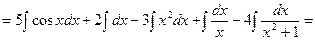
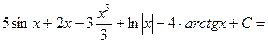
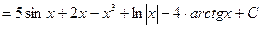 .
.
б) 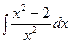 =
= 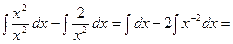
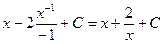 .
.
в)  =
= 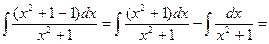
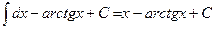 .p
.p
Дата: 2018-12-21, просмотров: 356.