1°. Постоянный множитель можно выносить за знак определённого интеграла, т.е.
,
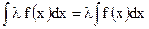где l - некоторое число.
2°. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
.
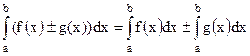3°. Если поменять местами пределы интегрирования, интеграл поменяет знак:
.
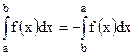4°. Если отрезок интегрирования разбит на части, то интеграл на всём отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых а, b, c:
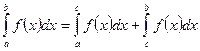
5°. Если пределы интегрирования совпадают, то определенный интеграл равен нулю.
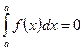
Пример №15. Найдите определенный интеграл, используя его свойства:
а)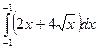 
; б) 
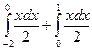; в)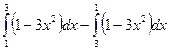 
;
г)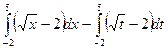 
.
r а)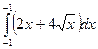 
=0, так как пределы интегрирования равны.
б) Так как верхний предел первого интеграла совпадает с нижним пределом второго интеграла и
-2 <0<1 то по свойству 20 имеем
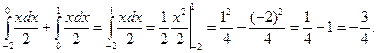
в) В силу равенств подынтегральных функций, поменяв местами пределы интегрирования второго интеграла, имеем
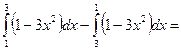
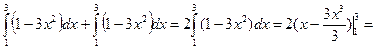
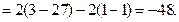
г)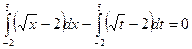 
, так как значение интеграла не зависит от обозначения переменной интегрирования. p
Пример №16. Вычислите определённый интеграл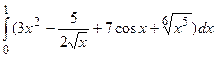 
r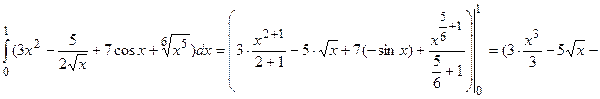 
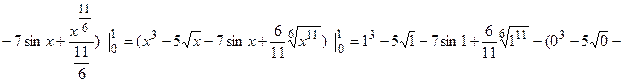
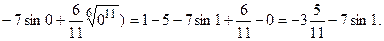p
Пример №17. Найдите значение интеграла: а)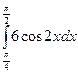 
; б)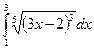 
.
Указание: Если функция имеет сложный аргумент в виде линейной функции одной переменной f(kx+b), то воспользуйтесь следующим правилом:
.
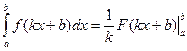r а)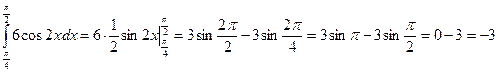 
б)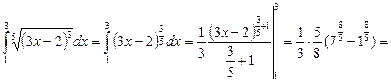 
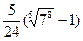.p
Вычисление площадей плоских фигур
Мы пришли к понятию определенного интеграла от задачи о площади криволинейной трапеции (фактически, используя метод интегральных сумм).
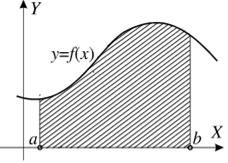
1. Если функция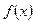 
принимает только неотрицательные значения (рис.1), то площадь 
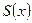под графиком функции на отрезке [a, b] может быть вычислена с помощью определенного интеграла:
.
|
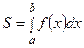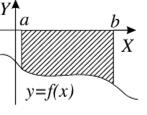2. Но функция может на некотором отрезке принимать и отрицательные значения, тогда интеграл по этому отрезку будет давать отрицательную площадь, что противоречит определению площади.
|
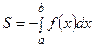
Можно вычислять площадь по формуле S=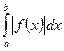 
. Это равносильно изменению знака функции в тех областях, в которых она принимает отрицательные значения.
|
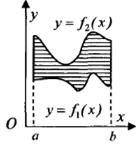
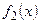, а снизу графиком функции 
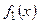(рис. 3), то можно пользоваться формулой
S=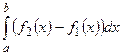 
,
так как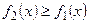 
.
Пример №18. Вычислите площадь фигуры, ограниченной линиями f(x)=-x2+3, у=0, x=-1, х=2.
r Построим графики заданных линий на плоскости:
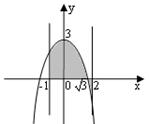f(x)=-x2+3 – парабола с вершиной в точке (0; 3), ветви которой направлены вниз. Парабола пересекает ось Ох в точках (- 
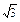;0) и ( 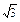;0).
у=0 – ось Ох.
х=-1 и х=2 – прямые, параллельные оси Оу.
В точке ( 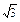;0) фигура разбивается на две части. Площадь верхней части, расположенной над осью Ох, вычисляется по формуле (1), площадь нижней части – по формуле (2):
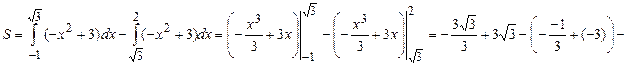
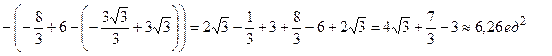p
Пример №19. Вычислить площадь фигуры, ограниченной линиям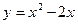и 
и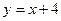 
.
r Построим область, ограниченную этими линиями: параболой и прямой.
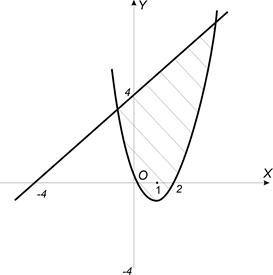
Найдем точки пересечения прямой и параболы, для чего решим систему:
, 
.
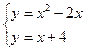
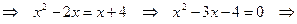
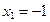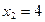Площадь фигуры, ограниченной двумя кривыми, вычисляется по формуле:
,
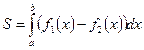где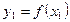 
- функция, график которой находится сверху, а 
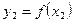- функция, график которой находится снизу.
В нашем случае пределы интегрирования равны:
, 
.
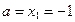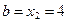Таким образом,
= 
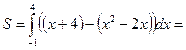
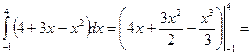
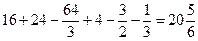ед2. p
Вопросы для повторения
1. Дайте определения предела функции в точке и на бесконечности.
2. Перечислите теоремы и следствия из них, на которых основано вычисление предела функции.
3. Что представляет собой число е?
4. Запишите формулы замечательных пределов.
5. Дайте определение односторонних пределов.
6. Перечислите необходимые и достаточные условия непрерывности функции в точке.
7. Какие элементарные функции непрерывны на всей числовой прямой?
8. Чему равны односторонние пределы функции в точке а, в которой функция непрерывна?
9. Какая функция называется непрерывной на промежутке?
10. Как называются точки, в которых условия непрерывности не выполнены?
11. Каким свойством обладает функция в точке устранимого разрыва?
12. Какие точки называются точками разрыва типа «скачок»?
13. Как называются точки, в которых функция имеет хотя бы один односторонний предел бесконечен или не существует?
14. Приведите примеры функций, имеющих разрывы.
15. Что называется приращением независимой переменной и приращением функции?
16. Запишите определение производной функции.
17. Как найти мгновенную скорость прямолинейного неравномерного движения?
18. Сформулируйте геометрический и физический смысл производной.
19. Как называется операция вычисления производной.
20. Запишите правила нахождения производной.
21. Какая функция называется дифференцируемой в точке и на отрезке?
22. Сформулируйте зависимость между непрерывностью и дифференцируемостью функции.
23. Как вычислить частное значение производной?
24. Запишите формулы производных обратных тригонометрических функций.
25. Сформулируйте определение производной n-го порядка
26. Сформулируйте правило нахождения производной сложной функции.
27. Какое действие называется интегрированием?
28. Какая функция называется первообразной для данной функции f(х)?
29. Чем отличаются друг от друга различные первообразные функции для данной функции f(х)?
30. Дайте определение неопределенного интеграла.
31. Какой геометрический образ соответствует неопределенному интегралу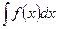 
?
32. Как проверяется результат интегрирования?
33.
34. Что называется определенным интегралом от функции f(x) на отрезке [a, b]?
35. Что в записи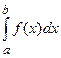 
означают: а) числа а и b; б) х; в) f(x); г) f(x)dx. Может ли быть a=b, a>b?
36. Сформулируйте основные свойства определённого интеграла.
37. В чём заключается геометрический смысл определённого интеграла?
38. В чем различия понятий определенного и неопределенного интегралов?
39. Выпишите формулу Ньютона — Лейбница и объясните ее смысл.
40. Запишите формулы вычисления площади плоских фигур с применением операции интегрирования, сопровождая записи графиками.
Дата: 2018-12-21, просмотров: 252.
