Тема 5.1. Вероятность, теоремы теории вероятностей

Понятие события и вероятности события. Достоверные и невозможные события. Классическое определение вероятностей. Основные понятия теории вероятностей. Теоремы теории вероятностей.

[1] Глава 7, стр. 276-293;

[2] Глава 10, стр. 221-234;

[3] Глава 16, стр. 371-381;

[4] Глава 16, стр. 257-266;

[5] Часть 2, Глава 5 стр. 176-187;

[6] Глава 1, стр. 15-57.

Основные понятия теории вероятностей.

Опыт, эксперимент, наблюдение явления называют испытанием. Результат, исход испытания называется событием. Для обозначения событий используются большие буквы латинского алфавита: А, В, С к т.д.

Два события называются несовместимыми, ес­ли наступление одного из них исключает возможность наступления другого. В противном случае события называются совместимыми.

Например, студент вытянул билет на экзамене. Тогда событие А, состоящее в том, что он знает вопросы билета, и событие В, состоящее в том, что он их не знает, являются несовместимы­ми.

Событие называется достоверным, если заведомо известно, что оно обязательно произойдет в условиях данного опыта или явления.

Событие называется невозможным, если оно не может произойти при выполнении определенного комплекса условий.

Например, событие, заключающееся в том, что из партии стандартных дета­лей будет взята стандартная деталь, является достоверным, а нестан­дартная — невозможным.

Два события, одно из которых обязательно должно произойти, но наступление одного исключает возможность наступления другого, называются противоположными.

Например, события «изделие удовлетворяет стандарту» и «изделие не удовлетворяет стандарту» — противоположные.

Событие, противоположное событию А, обозначается симво­лом .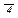

Например, стрелок производит один выстрел по мишени, которая имеет вид:

При этом возможны такие исходы: а) попадание в круг; б) попадание в прямоугольник; в) попадание не в круг и не в прямоугольник, которые, являются единственно возможными. Равновозможны они или нет - это другой вопрос, который требует специального рассмотрения.

События А, В, ..., М образуют полную систе­му, если они являются единственно возможными и несовместимыми ис­ходами некоторого опыта (явления).

Например, эектрические лампочки по сроку службы разобьем на следующие группы:

Взятая наудачу лампочка будет принадлежать той или иной груп­пе, что можно рассматривать соответственно как события. Эти события образуют полную систему.

Любые два противоположных со­бытия образуют полную систему.

Суммой ко­нечного числа событий называется новое событие, состоящее в наступле­нии хотя бы одного из них.

Произведением конечного числа со­бытий называется новое событие, состоящее в том, что они произой­дут все.

Например, если событие А состоит в попадании в круг, а событие В — в прямоугольник, то их сумма заключается в попадании в заштрихованную область (т. е. или в круг, или в прямоугольник), а произ­ведение — в попадании в общую часть круга и прямоугольника (на рисун­ке— в дважды заштрихованную область).

Согласно классическому определению вероятность события А вычисляется по формуле

Р(А) = ,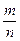

где n – число всех равновозможных, единственно возможных и несовместных исходов испытания; m – число исходов, благоприятствующих появлению события А.

Таким образом, нахождение вероятности события сводится к вычислению значений параметров n и m, а так как 0 ≤ m ≤ n, то 0≤ Р(А) ≤ 1.

Пример №34. Имеется 100 одинаковых деталей, среди которых 3 бракованных. Найти вероятность того, что взятая наудачу деталь окажется без брака.

r В этой задаче производится испытание – извлекается одна деталь. Число всех исходов испытания равно 100, т.к. может быть взята любая деталь из 100. Эти исходы несовместны, равновозможны и единственно возможны. Таким образом, n=100. Событие А состоит в появлении детали без брака. Всего в партии 97 деталей без брака, следовательно, число исходов, благоприятных появлению события А равно 97. Итак, m=97. Тогда Р(А)= 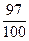 = 0,97.p

Для решения задач теории вероятности используют понятие числа сочетаний.

Числом сочетаний из n элементов по k в каждом, называют число соединений, в каждое из которых входит k элементов, взятых из данных n элементов и которые отличаются хотя бы одним элементом.

Число сочетаний из n по k обычно обозначается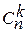

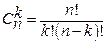
n! (то есть n факториал) означает произведение всех натуральных чисел от единицы до n, т.е.

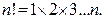
Например,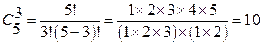

Правило произведения.

Если объект х может быть выбран m способами и после каждого такого выбора объект у в свою очередь может быть выбран n способами, то выбор упорядоченной пары <x,y> («х и у») может быть осуществлен m×n способами.

Пример№35. В партии из 20 деталей имеется 18 стандартных. Наудачу отобраны 5 деталей. Найти вероятность того, что среди отобранных деталей ровно 4 стандартных.

r Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 5 деталей из 20 деталей, то есть 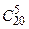 (числу сочетаний из 20 элементов по 5 элементов)

Число элементарных исходов, благоприятствующих интересующему нас событию (что среди 5 деталей ровно 4 стандартных) можно сосчитать следующим образом: четыре стандартных детали можно взять из 18 стандартных деталей 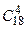способами; при этом оставшаяся одна деталь (5-4=1)должна быть нестандартной. Взять одну нестандартную деталь из (20-18=2) двух нестандартных можно  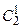способами.

Итак, число благоприятствующих исходов по правилу произведения равно

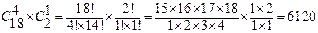
Общее число элементарных исходов

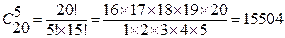
Искомая вероятность равна отношению числа исходов, благоприятствующих наступлению события к общему числу всех исходов.

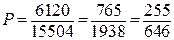.p