Запишем уравнение (7) в виде: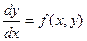 
или 
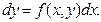
Такому уравнению можно придать следующую форму:
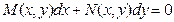(8)
Переменные х и у здесь равноправные.
Пусть
.
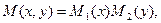
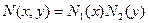Тогда уравнение (3) перепишется в виде:
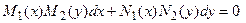. (8¢)
Полученное уравнение называется уравнением с разделяющимися переменными. Разделим уравнение на произведение функций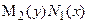 
. Данная операция называется разделением переменных.
В результате получили уравнение
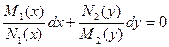. (9)
Уравнение (4) называется уравнением с разделенными переменными.
Соотношение F(x,y)=C, где
есть общий интеграл уравнения (9) и уравнения (8’).
Пример №20. Решите уравнение 2у5dy=(3-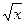 
)dx.
r Задано уравнение вида
f(y)dy=j(х)dх,
где f(y)= 2у5 и j(х) =(3-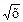 
) –данные функции. Интегрируя обе части уравнения, получаем: 
; 
; 
; 
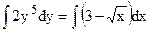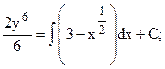
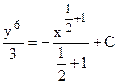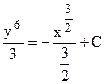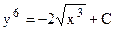. Общее решение найдём, выразив у: у= 
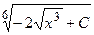.p
Пример №21. Найти общий интеграл дифференциального уравнения хy¢-y=0.
r Разделим переменные, записав предварительно, что у¢=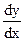 
: 
.
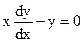Умножим выражение на dx: xdy-ydx=0.
Разделим уравнение на xy: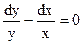 
. Получили уравнение с разделёнными переменными.
Общий интеграл: С=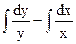 
=lny-lnx или С= 
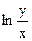. p
Линейныех однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейным неоднородным дифференциальным уравнением n –го порядка с постоянными коэффициентами называется уравнение вида
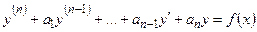, (10)
где а1, а2, …, а n – некоторые действительные числа.
Если f(x)=0, то уравнение называется линейным однородным:
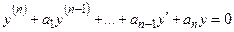. (11)
Однородное уравнение с той же левой частью, что и данное неоднородное, называется соответствующим ему.
Для нахождения частных решений однородного уравнения составляют характеристическое уравнение
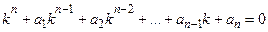, (12)
которое получается из линейного однородного уравнения заменой в нём производных искомой функции соответствующими степенями k, причём сама функция заменяется единицей.
Тогда общее решение дифференциального уравнения (11) строится в зависимости от характера корней уравнения (12) (См. Таблицу 1)
Таблица 1.
| Дифференциальное уравнение | у¢¢+py¢+qy=0 | ||
| Характеристическое уравнение | k2+pk+q=0 | ||
| Дискриминант | D>0 | D=0 | D<0 |
| Корни характеристического уравнения | k1¹k2 | k1=k2 | k1=a+bi k2=a-bi |
| Множества решений |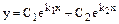 
| 
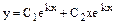
| у=еах(С1cosbx+C2sinbx) |
Пример №22. Найдите общее решение уравнения
1) 
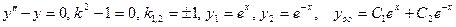
2) 
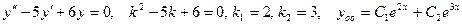
3) 
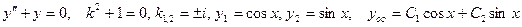
4) 
.
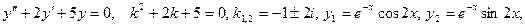
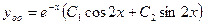5) 
.
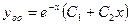Пример №23. Найдите частное решение уравнения у ¢¢ -2у ¢ +50=0, если у=1 и у ¢ =1 при х=0.
r Характеристическое уравнение k 2 -2 k +50=0 имеет корни у=1 ±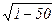 
=1 ± 7 i . Поэтому общее решение данного уравнения есть
y = ex ( C 1 cos 7 x + C 2 sin 7 x ).
Далее находим y ¢ = ex ( C 1 cos 7 x + C 2 sin 7 x )+ ex (-7 C 1 sin 7 x +7 C 2 cos 7 x ).
Подставив х=0, у=1 в выражение у, получим: 1=е0(С1с os 7 ´ 0+ C 2 sin 7 ´ 0) или 1=1(С1 ´ 1+С2 ´ 0), откуда С1=1. Затем, подставив х=0, у ¢ =-1, С1=1 в выражение для у ¢, получим:
-1= е0(1 ´ cos7´0+C2 ´ sin7´0)+e0(-7´1´ sin7´0+7´C2 ´ cos7´0) или -1=1+0+0+7С 2,
откуда С2=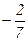 
.
Итак, искомое частное решение имеет вид y=ex(cos7x-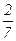 
sin7x).p
Вопросы для повторения
1. Какое уравнение называется дифференциальным? Приведите примеры.
2. Какая функция называется решением дифференциального уравнения?
3. Какое решение ДУ называют общим, а какое - частным?
4. Каков геометрический смысл общего и частного решений ДУ?
5. Может ли ДУ иметь конечное число решений?
6. Что такое порядок ДУ и как его определить?
7. Сколько постоянных интегрирования имеет общее решение ДУ первого порядка? Третьего порядка?
8. Как проверить, правильно ли найдено решение ДУ?
9. Каков общий вид ДУ с разделёнными и разделяющимися переменными?
10. Чем отличается уравнение с разделёнными переменными от уравнения с разделяющимися переменными?
11. Какая функция называется однородной функцией n-го измерения?
12. Какое дифференциальное уравнение первого порядка называется линейным?
13. Какое дифференциальное уравнение первого порядка называется однородным?
14. Каков общий вид дифференциального уравнения второго порядка?
15. Что такое общее решение дифференциального уравнения второго порядка?
16. Что называется линейным дифференциальным уравнением n-го порядка?
17. Какое линейное дифференциальное уравнение n-го порядка называется однородным?
18. Какова структура общего решения однородного линейного дифференциального уравнения?
19. Что такое характеристическое уравнение?
20. Как выглядит общее решение однородного линейного дифференциального уравнения второго порядка в случае, когда корни характеристического уравнения совпадают?
Раздел 2. Ряды
Дата: 2018-12-21, просмотров: 245.
