Тема 1.1. Дифференциальное и интегральное исчисление
Функции одной независимой переменной. Пределы. Непрерывность функций. Производная. Исследование функций.
Неопределенный интеграл. Методы интегрирования. Определенный интеграл. Вычисление определенного интеграла различными методами. Приложение интеграла к решению прикладных задач.
[1] Глава 1, стр. 4-151;
[2] Глава 3, стр. 55-59, Глава 7, стр. 145-164, Глава 8, стр. 179-203;
[3] Глава 4-6, стр.193-249, Глава 8-9, стр. 261-282;
[4] Глава 6-8, стр. 76-115, Глава 11-13, стр. 188-228;
[5] Часть 1, Глава 6-7 стр. 142-182, Глава 9-10 стр. 208-266.
Определение предела функции
|
Число b называется пределом функции f( x) при x®a, если для любого e>0 найдётся такое число d, что 
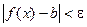как только 
.
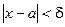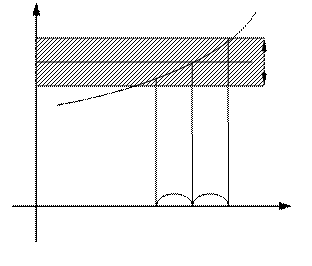
Если f(x)®b при х®а, то на графике функции y=f(x) это иллюстрируется следующим образом (рис.1): так как из неравенства |х-а|<d следует неравенство |f(х)-b|<е, то это значит, что для всех точек х, отстоящих от точки а не далее, чем на b, точки М графика функции y=f(x) лежат внутри полосы шириной 2e, ограниченной прямыми у=b-e и у=b+e.
Если f(x) стремится к пределу b при х, стремящемся к некоторому числу а так, что х принимает только значения, меньшие а, то пишут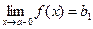 
и b1 называют пределом функции в точке а слева.
|
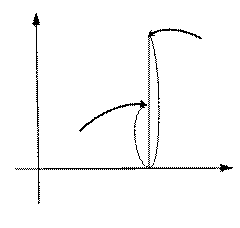
Если х принимает только значения, большие а, то пишут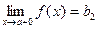 
и b2 называют пределом функции в точке а справа (рис. 2).
Если предел справа и предел слева существуют и равны, т.е. b1=b2=b, то b и будет пределом в смысле данного выше определения предела в точке а. И обратно, если существует предел функции b в точке а, то существуют пределы функции в точке а справа и слева и они равны.
Функция y=f(x) называется бесконечно малой в точке x=a, если ее предел в этой точке равен нулю: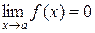 
.
Аналогично определяются бесконечно малые при x®±¥, x®a+0 и др.
Например, бесконечно малыми функциями являются:
1) f(x)=x2 при х®0; 2) у= x-2 при х®2 .
Функция y=f(x) называется бесконечно большой в точке x=a, если ее предел в этой точке равен бесконечности: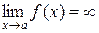 
.
Теорема. Если f( x) - бесконечно малая функция при x ® a, то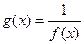 
- бесконечно большая функция при x ® a и наоборот.
Например, бесконечно большой является функция у=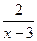 
при х®3, т.е. 
.
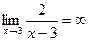Основные теоремы о пределах
1. Предел алгебраической суммы конечного числа переменных величин равен алгебраической сумме пределов слагаемых:
lim(x+y+…+t)=limx+limy+…+limt
Например,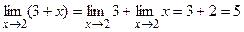 
.
2. Предел произведения конечного числа переменных величин равен произведению их пределов:
lim(x×y×…×t)=limx×limy×…×limt.
Следствие: Постоянный множитель можно выносить за знак предела:
Например,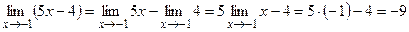 
.
3. Предел отношения двух переменных величин равен отношению пределов, если предел знаменателя не равен нулю:
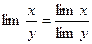, если limy¹0.
4. Предел целой положительной степени переменной величины равен той же степени предела этой же переменной:
limxn=(limx)n
Например,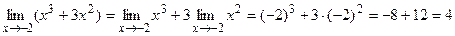 
.
Пример №1. Вычислить предел функции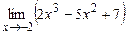 
непосредственным вычислением предела функции в точке.
Указание: В функцию, стоящую под знаком предела, подставить вместо х значение, к которому стремится аргумент.
r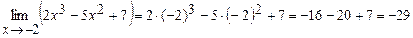 
p
Пример №2. Вычислить предел функции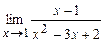 
разложением функции на множители.
Указания:
1. Выписать квадратный трёхчлен отдельно и приравнять его нулю ах2+bx+c=0.
2. Решить получившееся квадратное уравнение.
3. Разложить квадратный трёхчлен, стоящий под знаком предела, на множители по формуле
а(х-х1)(х-х2), где х1 и х2 –корни уравнения.
4. Сократить один из множителей.
5. Вычислить предел.
r Знаменатель функции, стоящей под знаком предела, представляет из себя квадратный трёхчлен. Разложим его на множители, решив квадратное уравнение:
х2-3х+2=0; D=(-3)2+4×1×(-2)=9-8=1; х1=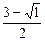 
=1; х2= 
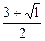=2.
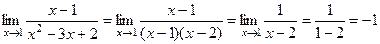.p
Пример №3. Вычислить предел функции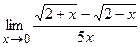 
.
r Умножим числитель и знаменатель на сумму корней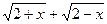 
, чтобы применить формулу сокращённого умножения (a+ b)( a- b)= a2- b2
= 
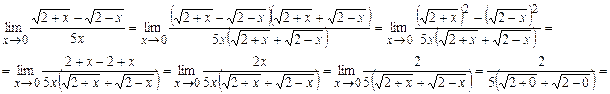
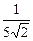.p
Дата: 2018-12-21, просмотров: 310.
