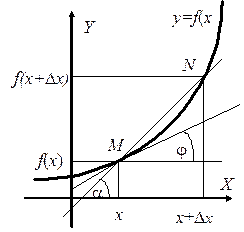|
|
Рассмотрим функцию y=f(x), непрерывную в некоторой окрестности точки x.
Пусть Dх - приращение (изменение) аргумента в точке x.
Обозначим через Dy=Df= f(x+Dx) – f(x) - приращение функции.
Отношение 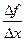 как видно из рисунка, равно тангенсу угла a, который составляет секущая MN кривой y = f(x) c положительным направлением горизонтальной оси координат.
как видно из рисунка, равно тангенсу угла a, который составляет секущая MN кривой y = f(x) c положительным направлением горизонтальной оси координат.
Если существует предел отношения 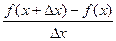 в точке Dx = 0, то он называется производной функции y = f(x) в точке x и обозначается y ¢ или f ¢ (x):
в точке Dx = 0, то он называется производной функции y = f(x) в точке x и обозначается y ¢ или f ¢ (x):
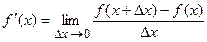 .
.
Нахождение производной функции y = f(x) называется дифференцированием.
Если для любого числа x из открытого промежутка (a, b) можно вычислить f ¢(x), то функция f(x) называется дифференцируемой на промежутке (a, b).
Пример №8. Найдите производную функции у=5х2-6 в точке х0=1, пользуясь непосредственно определением производной.
Используйте алгоритм:
1) Найти f(x0+Dx), т.е. в заданную функцию f(x) вместо х подставить х0+Dx;
2) Найти f(x0), т.е. в f(x) вместо х подставить х0;
3) Найти производную функции по формуле 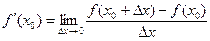
r Задана функция f(x)=5х2-6.
- Найдём f(x0+Dx)=5(x0+Dx)2-6=5(x02+2х0×Dx+(Dх)2)-6=5x02+10х0×Dx+5(Dх)2-6.
- Найдём f(x0)=5х02-6.
- Вычислим производную функции в точке х0:
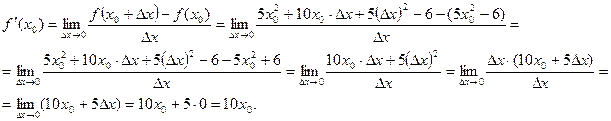
f ¢(x0)=10x0. f ¢(1)=10×1=10. p
Основные правила вычисления производной.
1. Производная постоянной равна нулю, т.е. 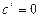 .
.
2. Производная аргумента равна 1, т.е. 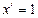 .
.
3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е.
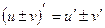 (3)
(3)
4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.
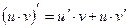 (4)
(4)
Следствие. Постоянный множитель можно выносить за знак производной:
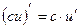 (5)
(5)
5. Производная частного двух дифференцируемых функций может быть найдена по формуле:
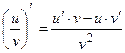 (6)
(6)
Таблица производных основных элементарных функций
1. C ¢=0, 9. 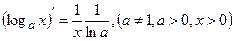 ,
,
2. (xn)¢=nxn-1, 10. 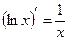 ,
,
3. 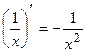 , 11.
, 11. 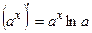 ,
,
4. 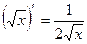 , 12.
, 12. 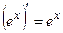 ,
,
5. 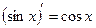 , 13.
, 13. 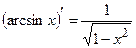 ,
,
6. 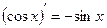 , 14.
, 14. 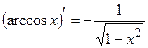 ,
,
7. 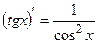 , 15.
, 15. 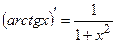 ,
,
8. 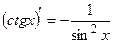 , 16.
, 16. 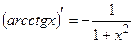 .
.
Пример №9. Найдите производную функции:
а) f(x)=3x4- 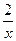 -5tgx+2sinx-2lnx+71; б) g(x)=(3x-6)
-5tgx+2sinx-2lnx+71; б) g(x)=(3x-6) 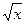 ; в)
; в) 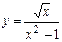 .
.
Указания: Используйте основные правила и формулы дифференцирования (таблицу производных):
r а) Здесь следует использовать правило дифференцирования суммы (разности) функций (3) и выносить постоянный коэффициент за знак производной (5).
f ¢(x)=(3x4- 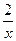 -5tgx+2sinx-2lnx+71)¢=(3x4)¢-
-5tgx+2sinx-2lnx+71)¢=(3x4)¢- 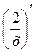 -(5tgx)¢+(2sinx)¢- (2lnx)¢+(71)¢= =3(x4)¢-2
-(5tgx)¢+(2sinx)¢- (2lnx)¢+(71)¢= =3(x4)¢-2 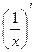 -5(tgx)¢+2(sinx)¢-2(lnx)¢+0=3×4x4-1-2×
-5(tgx)¢+2(sinx)¢-2(lnx)¢+0=3×4x4-1-2× 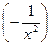 -5
-5 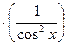 +2cosx-2
+2cosx-2 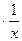 = =12x3+
= =12x3+ 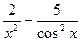 +2cosx-
+2cosx- 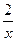 .
.
б) Следует использовать правило дифференцирования произведения функций (4) и таблицу производных.
g ¢(x)=(3x-6) ¢ 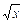 + (3x-6)(
+ (3x-6)( 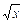 )¢=(3×1-0) ×
)¢=(3×1-0) × 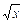 + (3x-6)
+ (3x-6) 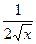 =3
=3 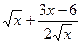 .
.
в) Используйте правило дифференцирования частного функций (6) и таблицу производных.
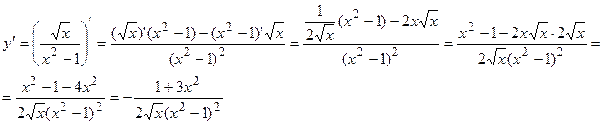
p
Дата: 2018-12-21, просмотров: 433.