СОДЕРЖАНИЕ
| Введение …………………………………………………………………………...... 1. Объем учебной дисциплины и виды учебной работы ………………………… 2. Тематический план ………………………………………………………………. 3. Литература ………………………………………………………………………... 4. Программа, методические указания и вопросы для самоконтроля…................ 4.1 Раздел 1. Математический анализ……………………………………………… 4.2 Раздел 2. Ряды …………………………………………………………………... 4.3 Раздел 3. Основы дискретной математики ……………………………………. 4.4 Раздел 4. Численные методы …………………………………………………... 4.5 Раздел 5. Основы теории вероятностей и математической статистики …….. 5. Варианты контрольной работы …………………………………………………. 6. Вопросы к зачету ………………………………………………………………… | 4 6 8 9 10 10 28 32 33 36 47 57 |
Введение
Настоящие методические указания составлены в соответствии с рабочей программой по дисциплине «Математика» для студентов специальности 08.02.08 Монтаж и эксплуатация оборудования и систем газоснабжения. Программа предназначена для реализации требований ФГОС к минимуму содержания и уровню подготовки выпускников по данной специальности среднего профессионального образования и является единой для всех форм обучения.
Формой обучения студента заочного отделения является самостоятельная работа над учебным материалом, которая состоит их следующих элементов: изучение материала по учебникам, решение задач, самопроверка, выполнение контрольных работ. В процессе самостоятельной работы студент может обращаться к преподавателю с вопросами для получения письменной или устной консультации. В помощь студентам заочного отделения организуются чтение лекций, практические занятия. Завершающим этапом изучения отдельных частей курса «Математика» является зачёт в соответствии с учебным планом по специальности.
Изучение материала по учебнику
Изучение материала по учебнику следует выполнять согласно указанным в программе курса темам. Изучая тот или иной вопрос темы по учебнику, целесообразно выполнять на бумаге все вычисления и вычерчивать имеющиеся в учебнике чертежи.
При самостоятельном изучении материала полезно вести конспект. В конспект по мере проработки материала рекомендуется вписывать определения, теоремы, формулы, уравнения и т.п. Поля конспектов могут послужить для выделения тех вопросов, на которые необходимо получить письменную или устную консультации. Ведение конспекта должно быть аккуратным, расположение текста хорошо продуманным.
Самопроверка
Опыт прочного усвоения материала темы показывает, что самопроверку проводить необходимо. В настоящем пособии приводятся для самопроверки вопросы, которые акцентируют внимание на наиболее важных, ключевых положениях темы. В процессе выполнения самопроверки необходимо избегать пользования учебником или конспектом. Желание обратиться к учебнику или конспекту показывает недостаточное усвоение материала темы.
Консультации
При изучении теоретического материала или при решении задач у студента могут возникнуть вопросы, разрешить которые самостоятельно не удается. В такой ситуации студенту следует обратиться к преподавателю для получения от него письменной или устной консультации. При этом необходимо точно указать вопрос, учебник и место в учебнике, где рассмотрен затрудняющий студента вопрос. Если непреодолимые затруднения возникли при решении задачи, то следует указать характер затруднения, привести план решения.
Контрольная работа
В процессе изучения курса студент должен выполнить одну контрольную работу, которая проходит рецензирование. По полученным результатам студент может сделать выводы о степени усвоения им соответствующего раздела курса, внести коррективы в процесс последующей самостоятельной работы по изучению теоретического материала.
К выполнению контрольной работы следует приступать после тщательного разбора имеющихся в учебнике и сборниках задач решений с ответами. В дополнение к предложенным задачам сборников в данном пособии рассмотрены некоторые примеры.
Контрольные работы должны выполняться самостоятельно, так как в противном случае рецензирование работы как диалог общения преподавателя – рецензента и студента с целью оказания последнему методической помощи не достигнет цели.
Контрольную работу следует выполнять в отдельной 12-листовой тетради, на внешней обложке указать фамилию, имя, отчество, курс, группа, вариант контрольной работы (образец взять у секретаря на отделении).
Выбор варианта зависит от номера в списке учебного журнала (определяется по последней цифре, например, №25 – вариант №5)
Работа выполняется чёрными, синими или фиолетовыми чернилами с полями для замечаний рецензента.
Решения задач должны быть подробными, без сокращения слов. Перед решением каждой задачи должно присутствовать условие – формулировка задания или задачи. Задачи располагать в порядке номеров, указанных в задании, не меняя этих номеров.
Чертежи можно выполнять от руки, но аккуратно.
Выполненная работа сдаётся секретарю отделения для регистрации и последующей проверки преподавателем.
Работу следует сдавать не менее чем за 2 недели до зачёта.
Если работа выполнена с ошибками, либо не в полном объёме, контрольная работа возвращается студенту с подробными замечаниями для доработки, при этом работа над ошибками выполняется в той же тетради.
Контрольная работа, выполненная небрежно, неразборчивым почерком, без соблюдения требований по оформлению возвращается студенту без проверки с указанием причин возврата на титульном листе.
Студент допускается к сдаче зачета при положительной аттестации контрольной работы.
Зачеты и экзамены
К зачету допускаются студенты, выполнившие контрольную работу (работы должны быть зачтены преподавателем-рецензентом). Определения, теоремы, правила должны формулироваться точно и с пониманием существа дела: решение задач должно выполняться без ошибок и уверенно. Только при выполнении этих условий знания студента могут быть признаны удовлетворяющими требованиям, предъявленными программой.
Цели и задачи учебной дисциплины – требования к результатам освоения учебной дисциплины «Математика»
В результате освоения учебной дисциплины обучающийся должен уметь:
- находить производные;
- вычислять неопределённые и определённые интегралы;
- решать прикладные задачи с использованием элементов – дифференциального и интегрального исчислений;
- решать простейшие дифференциальные уравнения;
- находить значения функций с помощью ряда Маклорена.
В результате освоения учебной дисциплины обучающийся должен знать:
- основные понятия и методы математического анализа, дискретной математики;
- основные численные методы решения прикладных задач;
- основные понятия теории вероятностей и математической статистики.
Изучение дисциплины «Математика» способствует формированию следующих общих и профессиональных компетенций:
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.
ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии для совершенствования профессиональной деятельности.
ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Ставить цели, мотивировать деятельность подчиненных, организовывать и контролировать их работу с принятием на себя ответственности за результат выполнения заданий.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Быть готовым к смене технологий в профессиональной деятельности.
ПК 1.1. Конструировать системы газораспределения и газопотребления.
ПК 1.2. Выполнять расчеты систем газораспределения и газопотребления.
ПК 1.3. Составлять спецификацию материалов и оборудования на системы газораспределения и газопотребления.
ПК 1.4. Осуществлять руководство другими работниками в рамках подразделения и взаимодействие с сотрудниками смежных подразделений при выполнении работ по проектированию газораспределения и газопотребления.
ПК 2.1. Организовывать и выполнять подготовку систем и объектов к строительству и монтажу.
ПК 2.2. Организовывать и выполнять работы по строительству и монтажу систем газораспределения и газопотребления.
ПК 2.3. Организовывать и выполнять производственный контроль качества строительно-монтажных работ.
ПК 2.4. Выполнять пусконаладочные работы систем газораспределения и газопотребления.
ПК 2.5. Руководство другими работниками в рамках подразделения и взаимодействие с сотрудниками смежных подразделений при выполнении работ по строительству и монтажу систем газораспределения и газопотребления.
ПК 3.1. Осуществлять контроль и диагностику параметров эксплуатационной пригодности систем газораспределения и газопотребления.
ПК 3.2. Осуществлять планирование работ, связанных с эксплуатацией и ремонтом систем газораспределения и газопотребления.
ПК 3.3. Организовывать производство работ по эксплуатации и ремонту систем газораспределения и газопотребления.
ПК 3.4. Организовывать производство работ по реконструкции систем газораспределения и газопотребления.
ПК 3.5. Осуществлять надзор и контроль за ремонтом и его качеством.
1. Объем учебной дисциплины и виды учебной работы
| Вид учебной работы | Объем часов |
| Максимальная учебная нагрузка (всего) | 96 |
| Обязательная аудиторная учебная нагрузка (всего) | 12 |
| в том числе: | |
| практические занятия | 10 |
| Самостоятельная работа обучающегося (всего) | 84 |
| в том числе: | |
| выполнение упражнений и задач по темам; работа с текстом конспекта, дополнительной литературы, выполнение домашней контрольной работы | 84 |
| Промежуточная аттестация в форме дифференцированного зачета | |
2. Тематический план
|
|
Наименование разделов и тем
Всего часов по учебному плану
Литература
Основные источники:
1. Григорьев С.Г., С.В. Иволгина, Математика. Учебник для ссузов – М.: Академия, 2011. - 416с.
2. Пехлецкий И. Д. Математика: учеб. для сред. проф. образования / И. Д. Пехлецкий. - 8-е изд., стер. - М. : Академия, 2011. - 304с.
3. Самойленко П.И., Богомолов Н.В. Математика: учебник для ссузов - М.: Дрофа, 2008.
Дополнительные источники:
4. Богомолов, Н. В. Практические занятия по математике : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2015. — 495 с.
5. Данко П.Е., Попов А.Г., Кожевников Г.Я. Высшая математика в упражнениях и задачах. т.I,II - М.: Высшая школа, 2008
6. Спирина, М. С. Теория вероятностей и математическая статистика: учеб. для сред.проф.образования / М. С. Спирина. - 2-е изд., стер. - М. : Академия, 2011. - 352с.
4. Программа, методические указания, вопросы для самоконтроля
Определение предела функции
|
 Число b называется пределом функции f( x) при x®a, если для любого e>0 найдётся такое число d, что
Число b называется пределом функции f( x) при x®a, если для любого e>0 найдётся такое число d, что 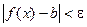 как только
как только 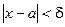 .
.
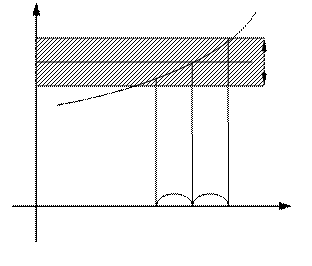
Если f(x)®b при х®а, то на графике функции y=f(x) это иллюстрируется следующим образом (рис.1): так как из неравенства |х-а|<d следует неравенство |f(х)-b|<е, то это значит, что для всех точек х, отстоящих от точки а не далее, чем на b, точки М графика функции y=f(x) лежат внутри полосы шириной 2e, ограниченной прямыми у=b-e и у=b+e.
Если f(x) стремится к пределу b при х, стремящемся к некоторому числу а так, что х принимает только значения, меньшие а, то пишут 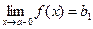 и b1 называют пределом функции в точке а слева.
и b1 называют пределом функции в точке а слева.
|
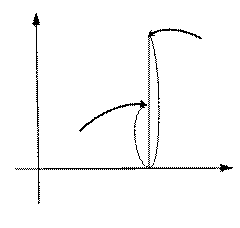 Если х принимает только значения, большие а, то пишут
Если х принимает только значения, большие а, то пишут 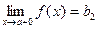 и b2 называют пределом функции в точке а справа (рис. 2).
и b2 называют пределом функции в точке а справа (рис. 2).
Если предел справа и предел слева существуют и равны, т.е. b1=b2=b, то b и будет пределом в смысле данного выше определения предела в точке а. И обратно, если существует предел функции b в точке а, то существуют пределы функции в точке а справа и слева и они равны.
Функция y=f(x) называется бесконечно малой в точке x=a, если ее предел в этой точке равен нулю: 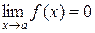 .
.
Аналогично определяются бесконечно малые при x®±¥, x®a+0 и др.
Например, бесконечно малыми функциями являются:
1) f(x)=x2 при х®0; 2) у= x-2 при х®2 .
Функция y=f(x) называется бесконечно большой в точке x=a, если ее предел в этой точке равен бесконечности: 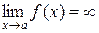 .
.
Теорема. Если f( x) - бесконечно малая функция при x ® a, то 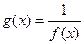 - бесконечно большая функция при x ® a и наоборот.
- бесконечно большая функция при x ® a и наоборот.
Например, бесконечно большой является функция у= 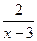 при х®3, т.е.
при х®3, т.е. 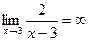 .
.
Основные теоремы о пределах
1. Предел алгебраической суммы конечного числа переменных величин равен алгебраической сумме пределов слагаемых:
lim(x+y+…+t)=limx+limy+…+limt
Например, 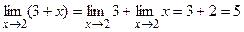 .
.
2. Предел произведения конечного числа переменных величин равен произведению их пределов:
lim(x×y×…×t)=limx×limy×…×limt.
Следствие: Постоянный множитель можно выносить за знак предела:
Например, 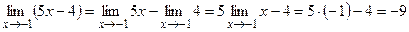 .
.
3. Предел отношения двух переменных величин равен отношению пределов, если предел знаменателя не равен нулю:
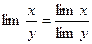 , если limy¹0.
, если limy¹0.
4. Предел целой положительной степени переменной величины равен той же степени предела этой же переменной:
limxn=(limx)n
Например, 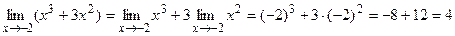 .
.
Пример №1. Вычислить предел функции 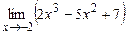 непосредственным вычислением предела функции в точке.
непосредственным вычислением предела функции в точке.
Указание: В функцию, стоящую под знаком предела, подставить вместо х значение, к которому стремится аргумент.
r 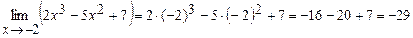 p
p
Пример №2. Вычислить предел функции 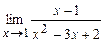 разложением функции на множители.
разложением функции на множители.
Указания:
1. Выписать квадратный трёхчлен отдельно и приравнять его нулю ах2+bx+c=0.
2. Решить получившееся квадратное уравнение.
3. Разложить квадратный трёхчлен, стоящий под знаком предела, на множители по формуле
а(х-х1)(х-х2), где х1 и х2 –корни уравнения.
4. Сократить один из множителей.
5. Вычислить предел.
r Знаменатель функции, стоящей под знаком предела, представляет из себя квадратный трёхчлен. Разложим его на множители, решив квадратное уравнение:
х2-3х+2=0; D=(-3)2+4×1×(-2)=9-8=1; х1= 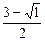 =1; х2=
=1; х2= 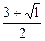 =2.
=2.
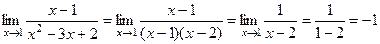 .p
.p
Пример №3. Вычислить предел функции 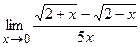 .
.
r Умножим числитель и знаменатель на сумму корней 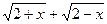 , чтобы применить формулу сокращённого умножения (a+ b)( a- b)= a2- b2
, чтобы применить формулу сокращённого умножения (a+ b)( a- b)= a2- b2
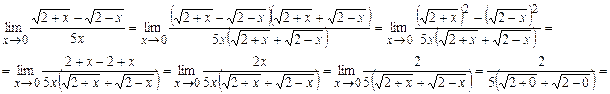
= 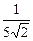 .p
.p
Замечательные пределы
Первый замечательный предел
Теорема. Предел функции 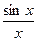 в точке х=0 существует и равен единице, т.е.
в точке х=0 существует и равен единице, т.е.
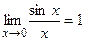 (1)
(1)
Предел (1) называется первым замечательным пределом и применяется при вычислении ряда других пределов. Рассмотрим несколько примеров на применение предела (1).
Пример №5. Найти предел функции 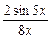 при х®0.
при х®0.
Указание: предел вида 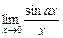 преобразуют так, чтобы использовать 1-й замечательный предел
преобразуют так, чтобы использовать 1-й замечательный предел 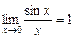 :
: 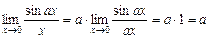 .
.
r 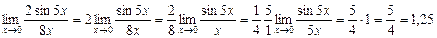 p
p
Второй замечательный предел
Теорема. Предел функции 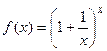 при х®¥ существует и равен е, т.е.
при х®¥ существует и равен е, т.е.
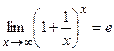 . (2)
. (2)
Или
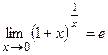
Предел (2) называется вторым замечательным пределом и применяется при вычислении ряда других пределов. e = 2.718281…
Число е - иррациональное число, е » 2,72.
Пример №6. Вычислить предел последовательности 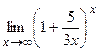 .
.
Указание: В пределах вида 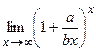 сделать замену
сделать замену 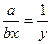 , откуда х=
, откуда х=  y.
y.
r 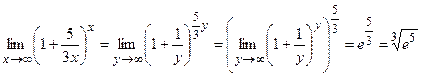 p
p
Пример №7. 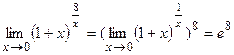
Определенный интеграл.
В математическом анализе, когда функция задана аналитически (в виде формулы) и интеграл удается свести к табличному, то определенный интеграл вычисляется с помощью таблиц неопределенных интегралов и формулы Ньютона-Лейбница, например:
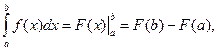
где [a; b] –отрезок интегрирования, а – нижний предел интегрирования, b – верхний предел интегрирования, f(x) - подынтегральная функция, f(x)dx – подынтегральное выражение, F(x) - первообразная, т.е. F¢(x)=f(x).
Вопросы для повторения
1. Дайте определения предела функции в точке и на бесконечности.
2. Перечислите теоремы и следствия из них, на которых основано вычисление предела функции.
3. Что представляет собой число е?
4. Запишите формулы замечательных пределов.
5. Дайте определение односторонних пределов.
6. Перечислите необходимые и достаточные условия непрерывности функции в точке.
7. Какие элементарные функции непрерывны на всей числовой прямой?
8. Чему равны односторонние пределы функции в точке а, в которой функция непрерывна?
9. Какая функция называется непрерывной на промежутке?
10. Как называются точки, в которых условия непрерывности не выполнены?
11. Каким свойством обладает функция в точке устранимого разрыва?
12. Какие точки называются точками разрыва типа «скачок»?
13. Как называются точки, в которых функция имеет хотя бы один односторонний предел бесконечен или не существует?
14. Приведите примеры функций, имеющих разрывы.
15. Что называется приращением независимой переменной и приращением функции?
16. Запишите определение производной функции.
17. Как найти мгновенную скорость прямолинейного неравномерного движения?
18. Сформулируйте геометрический и физический смысл производной.
19. Как называется операция вычисления производной.
20. Запишите правила нахождения производной.
21. Какая функция называется дифференцируемой в точке и на отрезке?
22. Сформулируйте зависимость между непрерывностью и дифференцируемостью функции.
23. Как вычислить частное значение производной?
24. Запишите формулы производных обратных тригонометрических функций.
25. Сформулируйте определение производной n-го порядка
26. Сформулируйте правило нахождения производной сложной функции.
27. Какое действие называется интегрированием?
28. Какая функция называется первообразной для данной функции f(х)?
29. Чем отличаются друг от друга различные первообразные функции для данной функции f(х)?
30. Дайте определение неопределенного интеграла.
31. Какой геометрический образ соответствует неопределенному интегралу 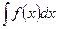 ?
?
32. Как проверяется результат интегрирования?
33.
34. Что называется определенным интегралом от функции f(x) на отрезке [a, b]?
35. Что в записи 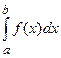 означают: а) числа а и b; б) х; в) f(x); г) f(x)dx. Может ли быть a=b, a>b?
означают: а) числа а и b; б) х; в) f(x); г) f(x)dx. Может ли быть a=b, a>b?
36. Сформулируйте основные свойства определённого интеграла.
37. В чём заключается геометрический смысл определённого интеграла?
38. В чем различия понятий определенного и неопределенного интегралов?
39. Выпишите формулу Ньютона — Лейбница и объясните ее смысл.
40. Запишите формулы вычисления площади плоских фигур с применением операции интегрирования, сопровождая записи графиками.
Вопросы для повторения
1. Какое уравнение называется дифференциальным? Приведите примеры.
2. Какая функция называется решением дифференциального уравнения?
3. Какое решение ДУ называют общим, а какое - частным?
4. Каков геометрический смысл общего и частного решений ДУ?
5. Может ли ДУ иметь конечное число решений?
6. Что такое порядок ДУ и как его определить?
7. Сколько постоянных интегрирования имеет общее решение ДУ первого порядка? Третьего порядка?
8. Как проверить, правильно ли найдено решение ДУ?
9. Каков общий вид ДУ с разделёнными и разделяющимися переменными?
10. Чем отличается уравнение с разделёнными переменными от уравнения с разделяющимися переменными?
11. Какая функция называется однородной функцией n-го измерения?
12. Какое дифференциальное уравнение первого порядка называется линейным?
13. Какое дифференциальное уравнение первого порядка называется однородным?
14. Каков общий вид дифференциального уравнения второго порядка?
15. Что такое общее решение дифференциального уравнения второго порядка?
16. Что называется линейным дифференциальным уравнением n-го порядка?
17. Какое линейное дифференциальное уравнение n-го порядка называется однородным?
18. Какова структура общего решения однородного линейного дифференциального уравнения?
19. Что такое характеристическое уравнение?
20. Как выглядит общее решение однородного линейного дифференциального уравнения второго порядка в случае, когда корни характеристического уравнения совпадают?
Раздел 2. Ряды
Основные понятия. Сходимость ряда.
Числовым рядом называется бесконечная последовательность чисел u1, u2,…, un,…, соединённых знаком сложения:
u1+ u2+…+ un....= 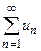 . (13)
. (13)
Числа u1, u2,…, un,…называются членами ряда, а член un - общим или n-м членом ряда.
Сумма n первых членов ряда Sn= u1+ u2+…+ un. называется n-й частичной суммой ряда.
Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.
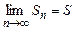 .
.
Число S называется суммой ряда.
Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.
Ряд, члены которого являются степенными функциями
с0+с1х+с2х2+…+с n xn+…, (14)
называется степенным рядом; числа с0,с1,с2,…с n называются коэффициентами степенного ряда.
Совокупность тех значений х, при которых степенной ряд (1) сходится, называется областью сходимости степенного ряда.
Любая функция, бесконечно дифференцируемая в интервале 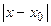 <r, т.е. х0-r<x<x0+r, может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора
<r, т.е. х0-r<x<x0+r, может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора
f(x)=f(x0)+ 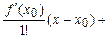
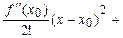 …+
…+ 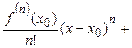 …,
…,
если в этом интервале выполняется условие
При х0=0 получается ряд Маклорена:
f(x)=f(0)+ 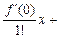
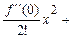 …+
…+ 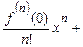 ….
….
Приведём разложения в ряд Маклорена следующих функций:
ех=1+х+ 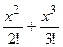 +…+
+…+ 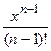 +…, при хÎ(-∞; ∞);
+…, при хÎ(-∞; ∞);
sinx=x- 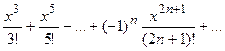 , xÎ(-¥ ¥);
, xÎ(-¥ ¥);
cosx=1- 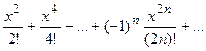 , хÎ(-¥; ¥);
, хÎ(-¥; ¥);
ln( x+1)= 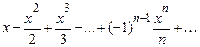 , хÎ(-1;1];
, хÎ(-1;1];
(1+х) a= 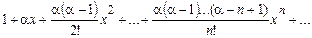 , хÎ(-1;1);
, хÎ(-1;1);
arcsinx= 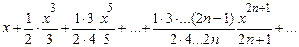 , xÎ[-1;1];
, xÎ[-1;1];
arctgx= 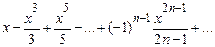 , xÎ[-1;1].
, xÎ[-1;1].
Пример №24. Разложить в степенной ряд по степеням х функцию:
а) 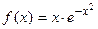 ; б) f( x)= ln(2+ x); в)
; б) f( x)= ln(2+ x); в) 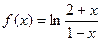
r а) Воспользуемся разложением ех=1+х+ 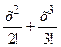 +… при хÎ(-∞; ∞).
+… при хÎ(-∞; ∞).
Заменяя в этом разложении х на (-х2) и умножая на х, получим:
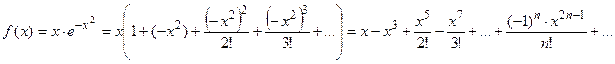
Полученный ряд является сходящимся также для любого хÎ(-∞; ∞). Действительно,
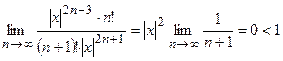 (Признак Даламбера).
(Признак Даламбера).
б) Сначала преобразуем эту функцию так: f(x)=ln(2+x)=ln(1+(1+x)). Обозначив (х+1)=у и используя разложение в ряд Маклорена функции f(y)=ln(1+y):
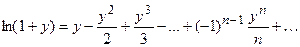 , заменим в нём у на (х+1); получим:
, заменим в нём у на (х+1); получим:
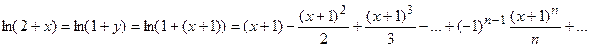 .
.
Учитывая, что Е=(-1; 1] – интервал сходимости используемого стандартного разложения, полученный ряд будет сходиться при значениях у, удовлетворяющих неравенству: -1<y≤1 или -1<x+1≤1, откуда находим интервал сходимости полученного ряда: -2<x≤0.
в) Данную функцию представим в виде
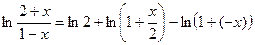 .
.
На основании разложения ln(1+x)=x- 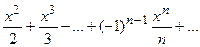 ,
, 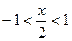 , т.е. при -2<x<2 можем записать
, т.е. при -2<x<2 можем записать
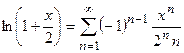 ,
,
аналогично при -1<-x≤1, т.е. при -1≤х<1
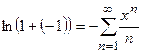 ,
,
следовательно,
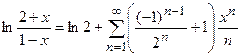 , хÎ[-1; 1). p
, хÎ[-1; 1). p
Пример №25.
Вычислить приближенно с точностью до 0,0001:
а)  ; б) ln0,6; в) ln5; г)
; б) ln0,6; в) ln5; г) 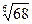 ; д) cos10°.
; д) cos10°.
r а) Для вычисления 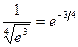 запишем ряд при х=-3/4, принадлежащим области сходимости (-∞; +∞):
запишем ряд при х=-3/4, принадлежащим области сходимости (-∞; +∞):
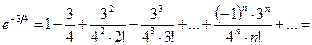 1- 0,75 + 0,28125 - 0,070312 + 0,013184 –
1- 0,75 + 0,28125 - 0,070312 + 0,013184 –
- 0,001978 + 0,000247 – 0,000026 + … .
Взяв первые семь членов разложения, мы допустим погрешность 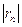 , не превышающую первого отброшенного члена ряда (по абсолютной величине), т.е.
, не превышающую первого отброшенного члена ряда (по абсолютной величине), т.е.
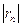 ≤0,000026<0,0001.
≤0,000026<0,0001.
Итак, складывая первые семь членов, получим
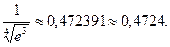
б) Для вычисления ln0,6 запишем ряд при х=- 0,4, входящем в область сходимости ряда (-1;1]:
ln0,6=ln(1+(-0,4))=-0,4- 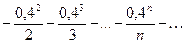 =
=
= - (0,4 + 0,08 + 0,021333 + 0,0064 + 0,002048 + 0,000683 + 0,000234 + 0,000082 +…).
Если в качестве ln0,6 взять первые восемь членов, мы допустим погрешность
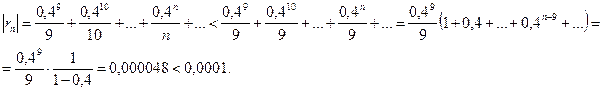
(мы учли, что сумма сходящегося геометрического ряда в скобках равна 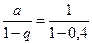 ).
).
Итак, складывая первые восемь членов, получим:
ln0,6 » - 0,510780»-0,5108.
в) Вычислить ln3=ln(1+2) с помощью ряда для функции у=ln(1+x) не представляется возможным, так как х=2 не входит в область сходимости ряда (-1; 1].
Воспользуемся рядом
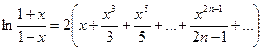 .
.
Этот ряд позволяет вычислить логарифмы любых чисел, так как при изменении х в интервале сходимости ряда (-1; 1) дробь 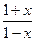 меняется в интервале (0; +∞).
меняется в интервале (0; +∞).
Так как решением уравнения 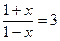 является число х=
является число х= 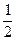 , то
, то 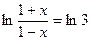 и
и
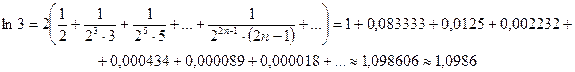
(суммируем семь первых членов ряда при заданной погрешности).
г) Представим 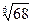 в виде
в виде 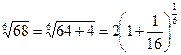 . Так как после проведенного преобразования
. Так как после проведенного преобразования 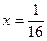 входит в область сходимости (-1; 1) биномиального ряда, то при
входит в область сходимости (-1; 1) биномиального ряда, то при 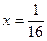 ,
, 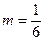 получим:
получим:
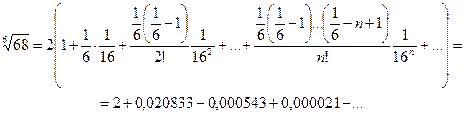
Для обеспечения данной в условии точности расчёта достаточно взять три члена, так как по следствию из признака Лейбница для сходимости знакочередующегося ряда погрешность 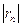 ≤0,000021<0,0001.
≤0,000021<0,0001.
Итак, 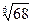 =2,020290»2,0203.
=2,020290»2,0203.
д) Для вычисления cos10°=cos 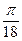 запишем ряд cosx при х=
запишем ряд cosx при х= 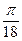 , принадлежащем области сходимости (-∞; +∞):
, принадлежащем области сходимости (-∞; +∞):
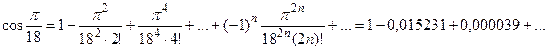
Необходимо взять два члена, так как при этом погрешность 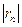 ≤0,000039<0,0001.
≤0,000039<0,0001.
Итак, cos10°»1-0,015231=0,984769»0,9848. p
Вопросы для повторения
1. Дайте определение числового ряда, суммы ряда. Что такое остаток ряда?
2. Какой ряд называется сходящимся?
3. Какой ряд называют степенным рядом?
4. Что такое область сходимости степенных рядов?
5. Ряды Тейлора и Маклорена.
6. Разложение элементарных функций в ряд Маклорена.
Множества.
Под множеством будем понимать совокупность (систему) каких-либо объектов произвольной природы, обладающих некоторым общим признаком.
Обозначение: А, B, C, D, …
Объекты, образующие множество, называются элементами множества и обозначаются соответствующими малыми буквами. Например, множество людей, множество городов России, множество целых чисел.
Некоторые множества имеют общепринятое обозначение:
N – множество натуральных чисел.
Z – множество целых чисел.
I – множество иррациональных чисел.
Q – множество рациональных чисел.
R – множество действительных чисел.
С – множество комплексных чисел.
Способы задания множеств:
- перечислением всех входящих в него объектов;
- описанием свойств, которыми должны обладать элементы множества. Такой способ называется аналитическим.
Например, множество M арабских цифр можно задать двояко: перечислением M={0,1,2,…,9} или посредством свойства M={x| х – арабская цифра}.
Множество, не содержащее ни одного элемента, называют пустым и обозначают Æ.
Количество элементов множества А называется мощностью множества и часто обозначают 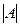 .
.
Пример 26. Мощность множества арабских цифр 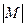 =10.
=10.
Если число элементов множества ограничено, то множество называют конечным, в противном случае – бесконечным.
Любую часть А (даже целую)множества В, выбранную по определённому признаку, называют подмножеством. Записывают
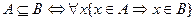 .
.
Пример 27. Справедливы следующие включения: NÍZ, ZÍQ, QÍR, RÍC,
{1; 4}Í{1;4;5;6;8}.
Операции над множествами
Рассмотрим исполнение отдельных операций над подмножествами A, B, C множества U.
а) АÈВ (объединение) – множество, состоящее из всех элементов множеств А и В, записанных в порядке возрастания и без повтора.
б) АÇВ (пересечение) – множество, составленное из общих (одинаковых) элементов множеств А и В.
в) А \ В (разность) – множество, составленное лишь из тех элементов множества А, которые не встречаются во множестве В.
г) 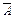 (дополнение) – множество элементов универсального множества U, которых нет в множестве А. За универсальное множество удобно взять множество целых чисел Z.
(дополнение) – множество элементов универсального множества U, которых нет в множестве А. За универсальное множество удобно взять множество целых чисел Z.
д) АDВ (симметрическая разность) – множество, состоящее из элементов множеств А и В, не включая их общие (одинаковые) элементы
Пример №28. Дано множество U={1;2;3;4;5;6;7;8;9;10} и множества А={2;3;4;5}, В={1;4;5;6;8} и С={4;6;7;9;10}. Записать множества:
1) АÈВ 2) АÇВ 3) АÈ(ВÇС) 4) 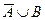 5) В\С 6)
5) В\С 6) 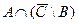
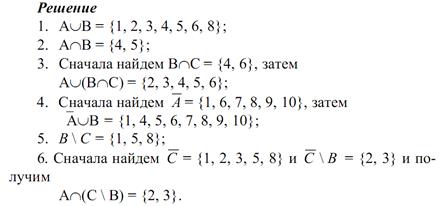
Вопросы для повторения
1. Дайте определение множества и приведите пример.
2. Какие способы задания множеств Вы знаете?
3. Перечислите основные числовые множества и их обозначения.
4. Что такое мощность множества?
5. Что такое подмножество? Приведите пример.
Раздел 4. Численные методы
Основные понятия.
Модуль (абсолютная величина) разности между точным числом х и его приближенным значением а называется абсолютной погрешностью приближенного значения числа х и обозначается через α, т. е. |х – а| = α.
Число а называется приближенным значением точного числа х с точностью до Dа, если абсолютная погрешность приближенного значения а не превышает Dа, т. е.
|х - а| ≤ Dа.
Число Dа называется границей абсолютной погрешности приближенного числа а.
Пример №29. Даны приближенные значения числа х= 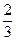 : а1 = 0,6; а2 = 0,66; а3= 0,67. Какое из этих приближений является лучшим?
: а1 = 0,6; а2 = 0,66; а3= 0,67. Какое из этих приближений является лучшим?
r Найдем абсолютную погрешность каждого приближенного значения.
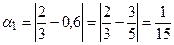 ,
,
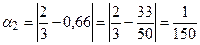 ,
,
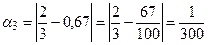 .p
.p
Относительной погрешностью 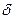 приближенного значения а числа х называется отношение абсолютной погрешности
приближенного значения а числа х называется отношение абсолютной погрешности  этого приближения к числу а, т.е.
этого приближения к числу а, т.е. 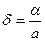 .
.
Число 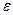 называется границей относительной погрешности, если
называется границей относительной погрешности, если 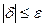 .
.
Действия над приближенными числами.
1. Сложение.
Граница абсолютной погрешности суммы (разности) приближенных значений чисел равна сумме границ абсолютных погрешностей этих чисел: 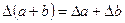 , где а и b – приближенные значения чисел,
, где а и b – приближенные значения чисел, 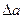 и
и  - границы абсолютных погрешностей соответствующих приближений.
- границы абсолютных погрешностей соответствующих приближений.
Граница относительной погрешности суммы вычисляется по формуле
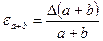 .
.
Пример №30. Электрическая цепь состоит из трёх последовательно соединённых проводников с сопротивлениями r1=6,8±0,05 (Ом), r2=4,3±0,05 (Ом), r3=3,575±0,0005 (Ом). Вычислите общее сопротивление цепи R. Найдите границы абсолютной DR и относительной eR погрешностей.
r R = 6,8+4,3+3,575=14,675; 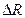 =0,05+0,05+0,0005=0,1005.
=0,05+0,05+0,0005=0,1005.
Граница абсолютной погрешности заключена в пределах 0,05<0,1005<0,5.
Граница относительной погрешности
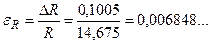
В процентах 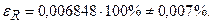 p
p
2. Вычитание.
Граница абсолютной погрешности разности двух приближенных значений чисел равна сумме границ абсолютных погрешностей этих чисел: 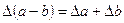 .
.
Граница относительной погрешности разности вычисляется по формуле
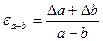 .
.
Пример №31. Вычислить разность двух приближенных значений чисел 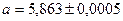 и
и 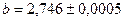 . Найти
. Найти 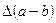 и
и 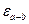 .
.
r Вычислим границу абсолютной погрешности разности a-b:
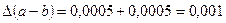 .
.
В приближенном значении разности цифра в разряде тысячных не может быть верной, так как 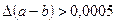 , следовательно,
, следовательно, 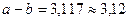 . Абсолютная погрешность разности 0,001. Находим относительную погрешность разности:
. Абсолютная погрешность разности 0,001. Находим относительную погрешность разности: 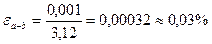 .p
.p
3. Умножение и деление.
Формулы для оценки границ абсолютной погрешности произведения (частного) сложны, поэтому сначала находят относительную погрешность произведения (частного), а затем границу абсолютной погрешности произведения (частного).
Формулы для границ абсолютной и относительной полгрешности приведены в таблице 2.
Таблица 2.
| Функция | Граница абсолютной погрешности | Граница относительной погрешности |
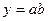
| 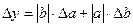
| 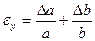
|
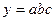
| 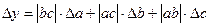
| 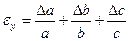
|
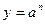
| 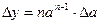
| 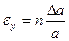
|
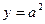
| 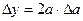
| 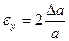
|
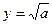
| 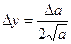
| 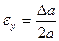
|
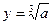
| 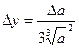
| 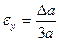
|
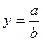
| 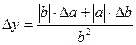
| 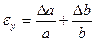
|
Пример №32. Найдите границы абсолютной и относительной погрешности вычисления площади жестяной пластины прямоугольной формы с измерениями а=12±0,05(см) и b=10±0,05(см)..
r Площадь прямоугольника S=a×b, следовательно, граница абсолютной погрешности вычисления площади
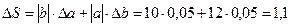 (см)
(см)
Граница относительной погрешности
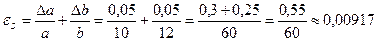 p
p
Пример №33. Вычислите силу тока I (A) в однородном участке цепи с напряжением U=120±0,5(В) при постоянном сопротивлении участка R=40±0,1(Ом). Найдите границы абсолютной DI и относительной eI погрешности вычисления.
r Имеем 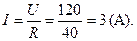
Граница абсолютной погрешности
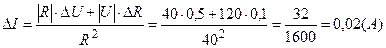
Границу относительной погрешности вычислим по формуле
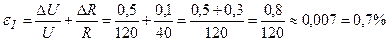 p
p
Вопросы для повторения
1. Что называется абсолютной погрешностью приближенного числа?
2. Что называется границей абсолютной погрешности?
3. Что называется относительной погрешностью приближенного числа?
4. Что называется границей относительной погрешности приближенного числа?
5. Что называется округлением десятичной дроби?
6. Что называется погрешностью округления?
7. Как производится округление с недостатком?
8. Как производится округление с избытком?
9. Как вычисляется граница абсолютной и относительной погрешности суммы приближенных значений чисел?
10. Как вычисляется граница абсолютной погрешности разности двух приближенных значений чисел?
11. Как вычисляется граница относительной погрешности разности приближенных значений чисел?
12. Как вычисляется граница абсолютной и относительной погрешности произведения и частного приближенных значений чисел?
13. Как вычисляется граница абсолютной и относительной погрешности степени приближенного значения числа?
14. Как вычисляется граница абсолютной и относительной погрешности квадратного и кубического корней из приближенных значений чисел?
Основные понятия теории вероятностей.
Опыт, эксперимент, наблюдение явления называют испытанием. Результат, исход испытания называется событием. Для обозначения событий используются большие буквы латинского алфавита: А, В, С к т.д.
Два события называются несовместимыми, если наступление одного из них исключает возможность наступления другого. В противном случае события называются совместимыми.
Например, студент вытянул билет на экзамене. Тогда событие А, состоящее в том, что он знает вопросы билета, и событие В, состоящее в том, что он их не знает, являются несовместимыми.
Событие называется достоверным, если заведомо известно, что оно обязательно произойдет в условиях данного опыта или явления.
Событие называется невозможным, если оно не может произойти при выполнении определенного комплекса условий.
Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.
Два события, одно из которых обязательно должно произойти, но наступление одного исключает возможность наступления другого, называются противоположными.
Например, события «изделие удовлетворяет стандарту» и «изделие не удовлетворяет стандарту» — противоположные.
Событие, противоположное событию А, обозначается символом 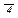 .
.
 Например, стрелок производит один выстрел по мишени, которая имеет вид:
Например, стрелок производит один выстрел по мишени, которая имеет вид:

При этом возможны такие исходы: а) попадание в круг; б) попадание в прямоугольник; в) попадание не в круг и не в прямоугольник, которые, являются единственно возможными. Равновозможны они или нет - это другой вопрос, который требует специального рассмотрения.
События А, В, ..., М образуют полную систему, если они являются единственно возможными и несовместимыми исходами некоторого опыта (явления).
Например, эектрические лампочки по сроку службы разобьем на следующие группы:
| Группа | А | В | С | Д | Е |
| Срок службы, ч | До 600 | 600-1200 | 1200-1800 | 1800-2400 | 2400 и более |
Взятая наудачу лампочка будет принадлежать той или иной группе, что можно рассматривать соответственно как события. Эти события образуют полную систему.
Любые два противоположных события образуют полную систему.
Суммой конечного числа событий называется новое событие, состоящее в наступлении хотя бы одного из них.
Произведением конечного числа событий называется новое событие, состоящее в том, что они произойдут все.
Например, если событие А состоит в попадании в круг, а событие В — в прямоугольник, то их сумма заключается в попадании в заштрихованную область (т. е. или в круг, или в прямоугольник), а произведение — в попадании в общую часть круга и прямоугольника (на рисунке— в дважды заштрихованную область).
Согласно классическому определению вероятность события А вычисляется по формуле
Р(А) = 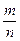 ,
,
где n – число всех равновозможных, единственно возможных и несовместных исходов испытания; m – число исходов, благоприятствующих появлению события А.
Таким образом, нахождение вероятности события сводится к вычислению значений параметров n и m, а так как 0 ≤ m ≤ n, то 0≤ Р(А) ≤ 1.
Пример №34. Имеется 100 одинаковых деталей, среди которых 3 бракованных. Найти вероятность того, что взятая наудачу деталь окажется без брака.
r В этой задаче производится испытание – извлекается одна деталь. Число всех исходов испытания равно 100, т.к. может быть взята любая деталь из 100. Эти исходы несовместны, равновозможны и единственно возможны. Таким образом, n=100. Событие А состоит в появлении детали без брака. Всего в партии 97 деталей без брака, следовательно, число исходов, благоприятных появлению события А равно 97. Итак, m=97. Тогда Р(А)= 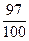 = 0,97.p
= 0,97.p
Для решения задач теории вероятности используют понятие числа сочетаний.
Числом сочетаний из n элементов по k в каждом, называют число соединений, в каждое из которых входит k элементов, взятых из данных n элементов и которые отличаются хотя бы одним элементом.
Число сочетаний из n по k обычно обозначается 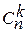
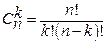
n! (то есть n факториал) означает произведение всех натуральных чисел от единицы до n, т.е.
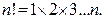
Например, 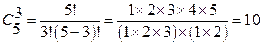
Правило произведения.
Если объект х может быть выбран m способами и после каждого такого выбора объект у в свою очередь может быть выбран n способами, то выбор упорядоченной пары <x,y> («х и у») может быть осуществлен m×n способами.
Пример№35. В партии из 20 деталей имеется 18 стандартных. Наудачу отобраны 5 деталей. Найти вероятность того, что среди отобранных деталей ровно 4 стандартных.
r Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 5 деталей из 20 деталей, то есть 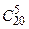 (числу сочетаний из 20 элементов по 5 элементов)
(числу сочетаний из 20 элементов по 5 элементов)
Число элементарных исходов, благоприятствующих интересующему нас событию (что среди 5 деталей ровно 4 стандартных) можно сосчитать следующим образом: четыре стандартных детали можно взять из 18 стандартных деталей 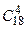 способами; при этом оставшаяся одна деталь (5-4=1)должна быть нестандартной. Взять одну нестандартную деталь из (20-18=2) двух нестандартных можно
способами; при этом оставшаяся одна деталь (5-4=1)должна быть нестандартной. Взять одну нестандартную деталь из (20-18=2) двух нестандартных можно 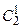 способами.
способами.
Итак, число благоприятствующих исходов по правилу произведения равно
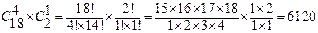
Общее число элементарных исходов
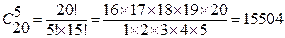
Искомая вероятность равна отношению числа исходов, благоприятствующих наступлению события к общему числу всех исходов.
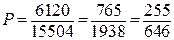 .p
.p
Формула полной вероятности.
Пусть событие А может произойти лишь при условии появления одного из n попарно несовместных событий 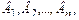 образующих полную группу событий. События
образующих полную группу событий. События 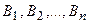 будем называть гипотезами для события А. Тогда вероятность события А
будем называть гипотезами для события А. Тогда вероятность события А
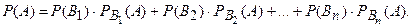
Пример №43. Магазин получил две равные по количеству партии обуви в одинаковых упаковках. Известно, что в среднем 8% обуви в первой партии и 14% во второй партии имеют определённые дефекты отделки верха. Какова вероятность того, что взятая наугад в магазине пара обуви будет иметь дефект отделки верха?
r Эта задача решается с применением формулы полной вероятности.
Введём обозначение событий. Пусть:
- событие А состоит в том, что наугад выбранная пара обуви имеет дефект отделки верха;
- гипотеза H 1 состоит в том, что наугад выбранная пара обуви взята из первой партии;
- гипотеза H2 состоит в том, что наугад выбранная пара обуви взята из второй партии.
Вероятность события А найдём, пользуясь формулой полной вероятности:
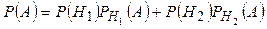
Так как по объёму обе партии одинаковые, то вероятности Р(H1) и Р(H2) равны между собой и Р(H1)=Р(H2)=0,5.
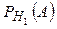 - условная вероятность того, что наугад взятая пара обуви из первой партии имеет дефект отделки верха. По условию задачи
- условная вероятность того, что наугад взятая пара обуви из первой партии имеет дефект отделки верха. По условию задачи  .
.
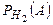 - условная вероятность того, что наугад взятая пара обуви из второй партии имеет дефект отделки верха.
- условная вероятность того, что наугад взятая пара обуви из второй партии имеет дефект отделки верха.
По условию задачи 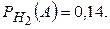 .
.
Подставляем все вероятности в формулу полной вероятности:
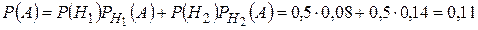 .p
.p
Вопросы для повторения
1. Сформулируйте классическое определение вероятности. В чем ограниченность этого определения?
2. В чем различие между вероятностью и относительной частотой?
3. Дайте определение суммы событий. Приведите примеры: суммы двух несовместных событий; суммы двух совместных событий.
4. Сформулируйте и докажите теорему о сложении вероятностей несовместных событий.
5. Дайте определение произведения событий. Приведите примеры: произведения двух независимых событий; произведения двух зависимых событий.
6. Что такое условная вероятность?
7. Сформулируйте теорему об умножении вероятностей для двух событий (общий случай). Какую форму принимает эта теорема в случае, когда события независимы?
Основные понятия.
Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.
Примеры. 1). Число очков, выпавших при однократном бросании игральной кости, есть случайная величина, она может принять одно из значений: 1, 2, 3, 4, 5, 6;
2) прирост массы домашнего животного за месяц есть случайная величина, которая может иметь значение из некоторого числового промежутка;
3) число родившихся мальчиков среди пяти новорожденных есть случайная величина, которая может принять значения 0, 1, 2, 3, 4, 5;
4) расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина, возможные значения которой принадлежат некоторому промежутку.
Случайные величины обычно обозначают прописными буквами X, Y, Z, а их возможные значения — соответствующими строчными буквами х, у, z. Например, если случайная величина А имеет три возможных значения, то они будут обозначены так:
х1, х2, х3.
Случайная величина, принимающая конечное число значений называется дискретной случайной величиной. Дискретная случайная величина Х может быть задана рядом распределения. Рядом распределения называется совокупность всех возможных значений х i и соответствующих им вероятностей р i = Р ( Х = х i ), он может быть задан в виде таблицы:
| х i | х1 | х2 | . . . | х n |
| р i | р1 | р2 | . . . | р n |
При этом вероятности р i удовлетворяют условию  р i = 1.
р i = 1.
Например, закон распределения случайной величины, равной выпавшему числу при бросании кубика выглядит следующим образом:
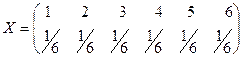 .
.
Графическое изображение ряда распределения называется многоугольником распределения. Для его построения возможные значения случайной величины (х i) откладываются по оси абсцисс, а вероятности р i - по оси ординат; точки c координатами (х i, р i) соединяются прямыми отрезками.
Пример 44. В урне находятся 3 черных и 2 белых шара. Из урны наугад извлекают 2 шара. Случайная величина X - число белых шаров среди извлеченных. Записать закон распределения случайной величины X, сделать проверку. Построить многоугольник распределения.
r Случайная величина может принять значения 0, 1, 2. Число возможных исходов опыта равно
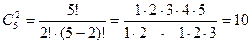 .
.
Вероятность того, что X = 0, есть вероятность события «извлечены 2 черных шара». Число благоприятствующих исходов равно 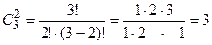 . Следовательно P(X = 0) =0,3.
. Следовательно P(X = 0) =0,3.
Вероятность того, что X = 1, есть вероятность события «извлечен 1 белый и 1 черный шар». Число благоприятствующих исходов равно 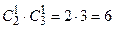 . Следовательно P(X = 1) =0,6.
. Следовательно P(X = 1) =0,6.
Вероятность того, что X = 2, есть вероятность события «извлечены 2 белых шара». Число благоприятствующих исходов равно 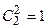 . Следовательно P(X = 1) =0,1.
. Следовательно P(X = 1) =0,1.
Закон распределения случайной величины X = 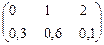
Проверим правильность построения закона распределения: 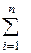 р i =0,3+0,6+0,1=1.
р i =0,3+0,6+0,1=1.
Закон построен верно.
Многоугольник распределения будет иметь вид:
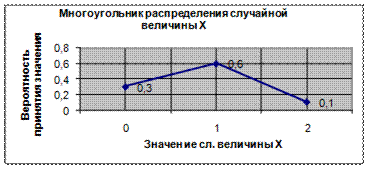 p
p
Вопросы для повторения
1. Дайте определения случайной величины, приведите пример.
2. Какая случайная величина называется дискретной? Приведите пример.
3. Каким образом задается дискретная случайная величина?
4. Как называется графическое представление дискретной случайной величины? Приведите пример.
Вопросы для повторения
1. Дайте определение математического ожидания ДСВ, поясните его сущность, запишите формулу.
2. Какими свойствами обладает математическое ожидание ДСВ?
3. Что такое дисперсия ДСВ? В чем заключается её сущность?
4. Запишите свойства дисперсии ДСВ.
5. Дайте определение среднеквадратического отклонения ДСВ, поясните его сущность.
Варианты контрольной работы
Вариант 1
1. Вычислите пределы функций:
а) 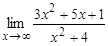 ; б)
; б) 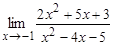 ; в)
; в) 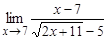 ; г)
; г) 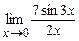 ; д)
; д) 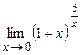 .
.
2. Найдите производные функций. В пункте а) найдите производную третьего порядка:
а) f(x)=x7-3x5+2sinx-2; б) g(x)=x 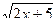 ; в) f(x)=
; в) f(x)= 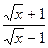 ; г)
; г) 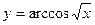 .
.
3. Найдите неопределенные интегралы и вычислите определенный интеграл:
а) 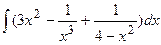 ; б)
; б) 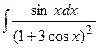 ; в)
; в) 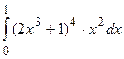 .
.
4. Вычислите площадь фигуры, ограниченной указанными линиями. Сделайте чертеж.
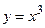 ;
; 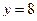 ;
; 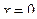 .
.
5. Решите указанные дифференциальные уравнения 1-го и 2-го порядков
а) xdy-4ydx=0;
б) у¢¢+y=0, найдите частное решение, если у=1, у´=0 при х=0.
6. Для множеств U=Z, А={ -2, 0, 2, 4} и B={0, 1, 2, 3, 4} найдите: а) АÈВ, б) АÇВ, в) А \ В, г) 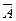 , д) АDВ.
, д) АDВ.
7. а) Разложите в степенной ряд по степеням х функцию у=sin5x;
б) Вычислите приближенно с точностью до 0,0001 значение выражения 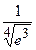 .
.
8. Вычислите силу тока I (A) в однородном участке цепи с напряжением U=120±0,5 (В) при постоянном сопротивлении участка R=20±0,4 (Ом). Найдите абсолютную DI и относительную eI погрешности.
9. В партии, состоящей из 20 радиоприемников, 6 неисправны. Из партии наудачу отбираются 3 приемника. Какова вероятность того, что в число отобранных войдут один неисправный и два исправных приемника?
10. Испытываемый прибор состоит из трех малонадежных элементов. Отказы элементов за некоторое время Т независимы, а их вероятности равны соответственно Р1 = 0,2, Р2 = 0,2, Р3 = 0,25. Составьте закон распределения и найдите математическое ожидание и дисперсию числа отказывающих за время Т элементов.
Вариант 2
1. Вычислите пределы функций:
а) 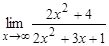 ; б)
; б) 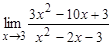 ; в)
; в) 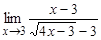 ; г)
; г) 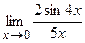 ; д)
; д) 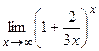 .
.
2. Найдите производные функций. В пункте а) найдите производную третьего порядка:
а) f(x)=4x+2x5+5cosx-1; б) g(x)=x3×4lnx; в) f(x)= 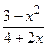 ; г) y=arctg(2x).
; г) y=arctg(2x).
3. Найдите неопределенные интегралы и вычислите определенный интеграл:
а) 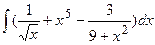 ; б)
; б) 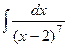 ; в)
; в) 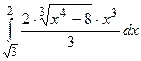 .
.
4. Вычислите площадь фигуры, ограниченной указанными линиями. Сделайте чертеж.
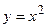 ;
; 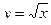 .
.
5. Решите указанные дифференциальные уравнения 1-го и 2-го порядков
а) (1+y2)dx=xydy;
б) у¢¢+3y´+2y=0, найдите частное решение, если у=-1, у´=3 при х=0.
6. Для множеств U=Z, А={ -5, -3, -2, 1} и B={0, 1, 2, 4} найдите: а) АÈВ, б) АÇВ, в) А \ В, г) 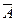 , д) АDВ.
, д) АDВ.
7. а) Разложите в степенной ряд по степеням х функцию у=е-3х;
б) Вычислите приближенно с точностью до 0,0001 значение выражения ln1,4.
8. Вычислите силу тока I (A) в однородном участке цепи с напряжением U=130±0,5 (В) при постоянном сопротивлении участка R=65±0,4 (Ом). Найдите абсолютную DI и относительную eI погрешности.
9. Радист дважды вызывает своего корреспондента. Вероятность того, что будет принят первый вызов, равна 0.2, второй – 0.3. События, состоящие в том, что вызовы будут услышаны, независимы. Найдите вероятность того, что вызовы будут услышаны не менее одного раза.
10. В партии из 21 детали содержатся 7 деталей второго сорта, остальные первого. Отобраны случайным образом 4 детали. Составьте закон распределения и найдите математическое ожидание и дисперсию числа деталей первого сорта в выборке.
Вариант 3
1. Вычислите пределы функций:
а) 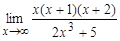 ; б)
; б) 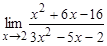 ; в)
; в) 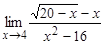 ; г)
; г) 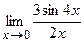 ; д)
; д) 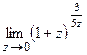 .
.
2. Найдите производные функций. В пункте а) найдите производную третьего порядка:
а) f(x) =2 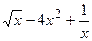 ; б) y=(
; б) y=( 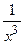 +1)(2x-3); в) j(x)=
+1)(2x-3); в) j(x)= 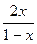 ; г)
; г) 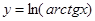 .
.
3. Найдите неопределенные интегралы и вычислите определенный интеграл:
а) 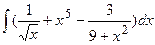 ; б)
; б) 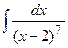 ; в)
; в) 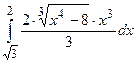 .
.
4. Вычислите площадь фигуры, ограниченной указанными линиями. Сделайте чертеж.
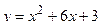 ;
; 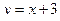 .
.
5. Решите указанные дифференциальные уравнения 1-го и 2-го порядков
а) 5xdy+ydx=0;
б) у¢¢+2y´+5y=0, найдите частное решение, если у=1, у´=1 при х=0.
6. Для множеств U=Z, А={ 11, 13, 20, 24} и B={0, 11, 22, 25} найдите: а) АÈВ, б) АÇВ, в) А\В, г) 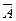 , д) АDВ.
, д) АDВ.
7. а) Разложите в степенной ряд по степеням х функцию у=cos2x;
б) Вычислите приближенно с точностью до 0,0001 значение выражения ln1,3.
8. Вычислите силу тока I (A) в однородном участке цепи с напряжением U=220±0,5 (В) при постоянном сопротивлении участка R=40±0,4 (Ом). Найдите абсолютную DI и относительную eI погрешности.
9. Двигатель может работать в нормальном и форсированном режимах. За время работы двигателя нормальный режим наблюдается в 80 % случаев, а форсированный — в 20 %. Вероятность выхода из строя при нормальном режиме равна 0.01, а при форсированном — 0.03. Найдите полную вероятность выхода двигателя из строя за время работы.
10. Используемый прибор состоит из трех малонадежных элементов. Отказы элементов за некоторое время Т не зависимы, а их вероятности равны соответственно Р1 = 0,1, Р2 = 0,2, Р3 = 0,3. Составьте закон распределения и найдите математическое ожидание и дисперсию числа не отказавших элементов.
Вариант 4
1. Вычислите пределы функций:
а) 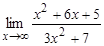 ; б)
; б) 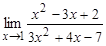 ; в)
; в) 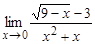 ; г)
; г) 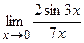 ; д)
; д) 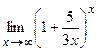 .
.
2. Найдите производные функций. В пункте а) найдите производную третьего порядка:
a) y= 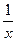 -6x+x10; б) f(x) = (3x2-2)3cosx; в) g(x) =
-6x+x10; б) f(x) = (3x2-2)3cosx; в) g(x) = 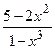 ; г) y=arcsin(lnx).
; г) y=arcsin(lnx).
3. Найдите неопределенные интегралы и вычислите определенный интеграл:
а) 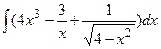 ; б)
; б) 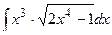 ; в)
; в) 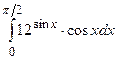 .
.
4. Вычислите площадь фигуры, ограниченной указанными линиями. Сделайте чертеж.
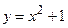 ;
; 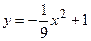 ;
; 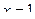 .
.
5. Решите указанные дифференциальные уравнения 1-го и 2-го порядков
а) 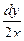 +2ydx=0;
+2ydx=0;
б) у¢¢+4y=0, найдите частное решение, если у=1, у´=-2 при х=p/4.
6. Для множеств U=Z, А={-3, -1, 0, 4} и B={0, 1, 3, 4} найдите: а) АÈВ, б) АÇВ, в) А \ В, г) 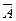 , д) АDВ.
, д) АDВ.
7. а) Разложите в степенной ряд по степеням х функцию y=ln(1+3x);
б) Вычислите приближенно с точностью до 0,0001 значение выражения 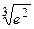 .
.
8. Вычислите силу тока I (A) в однородном участке цепи с напряжением U=160±0,5 (В) при постоянном сопротивлении участка R=80±0,4 (Ом). Найдите абсолютную DI и относительную eI погрешности.
9. Вероятность выхода станка из строя в течение рабочего дня 0,05. Какова вероятность того, что за пять дней станок ни разу не выйдет из строя?
10. В партии из 7 деталей имеется 5 деталей первого сорта. Наудачу отобраны 3 детали. Составьте закон распределения и найдите математическое ожидание и дисперсию числа деталей первого сорта среди отобранных.
Вариант 5
1. Вычислите пределы функций:
а) 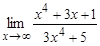 ; б)
; б) 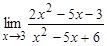 ; в)
; в) 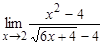 ; г)
; г) 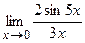 ; д)
; д) 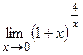 .
.
2. Найдите производные функций. В пункте а) найдите производную третьего порядка:
а) f(x)= 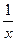 +4ctgx-x3; б) y=etgx ×(x4-1); в) f(x)=
+4ctgx-x3; б) y=etgx ×(x4-1); в) f(x)= 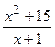 ; г) y=arcsinx3.
; г) y=arcsinx3.
3. Найдите неопределенные интегралы и вычислите определенный интеграл:
а) 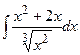 ; б)
; б) 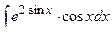 ; в)
; в) 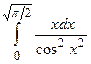 .
.
4. Вычислите площадь фигуры, ограниченной указанными линиями. Сделайте чертеж.
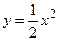 ;
; 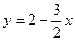 .
.
5. Решите указанные дифференциальные уравнения 1-го и 2-го порядков
а) ydx+ctgxdy=0;
б) у¢¢+4y´+4у=0, найдите частное решение, если у=1, у´=-1 при х=0.
6. Для множеств U=Z, А={ -5, -4, -3, 1} и B={-3, 1, 2, 3} найдите: а) АÈВ, б) АÇВ, в) А \ В, г) 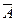 , д) АDВ.
, д) АDВ.
7. а) Разложите в степенной ряд по степеням х функцию y=sin(-6x);
б) Вычислите приближенно с точностью до 0,0001 значение выражения 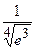 .
.
8. Вычислите силу тока I (A) в однородном участке цепи с напряжением U=80±0,5 (В) при постоянном сопротивлении участка R=10±0,4 (Ом). Найдите абсолютную DI и относительную eI погрешности.
9. Прибор состоит из 10 узлов. Надежность (вероятность безотказной работы в течение времени Т) для каждого узла равна 0,9. Узлы выходят из строя независимо один от другого. Найдите вероятность того, что за время Т: а) откажет хотя бы один узел; 6) откажет ровно один узел.
10. Имеется 4 заготовки для одной и той же детали. Вероятность изготовления годной детали из каждой заготовки равна 0,7. Составьте закон распределения и найдите математическое ожидание и дисперсию числа заготовок, оставшихся после изготовления первой годной детали.
Вариант 6
1. Вычислите пределы функций:
а) 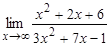 ; б)
; б) 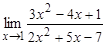 ; в)
; в) 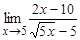 ; г)
; г) 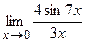 ; д)
; д) 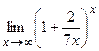 .
.
2. Найдите производные функций. В пункте а) найдите производную третьего порядка:
а) y= 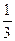 x3+x2-6tgx; б) y=2x×
x3+x2-6tgx; б) y=2x× 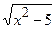 ; в) f(x)=
; в) f(x)= 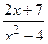 ; г) y=arctg(x2).
; г) y=arctg(x2).
3. Найдите неопределенные интегралы и вычислите определенный интеграл:
а) 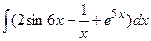 ; б)
; б) 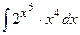 ; в)
; в) 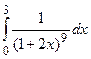 .
.
4. Вычислите площадь фигуры, ограниченной указанными линиями. Сделайте чертеж.
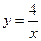 ;
; 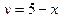 .
.
5. Решите указанные дифференциальные уравнения 1-го и 2-го порядков
а) 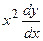 -2y=0;
-2y=0;
б) у¢¢-10у´+25y=0, найдите частное решение, если у=2, у´=8 при х=0.
6. Для множеств U=Z, А и B найдите: а) АÈВ, б) АÇВ, в) А \ В, г) 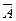 , д) АDВ.
, д) АDВ.
А={ 1, 4, 5, 7} и B={0, 1, 2, 3}.
7. а) Разложите в степенной ряд по степеням х функцию у=е-2х;
б) Вычислите приближенно с точностью до 0,0001 значение выражения ln0,8.
8. Вычислите силу тока I (A) в однородном участке цепи с напряжением U=210±0,5 (В) при постоянном сопротивлении участка R=60±0,6 (Ом). Найдите абсолютную DI и относительную eI погрешности.
9. Станок одну треть своего времени обрабатывает деталь А и две трети - деталь В. При обработке детали А он простаивает 10% времени, детали В - 15%. Какова вероятность застать станок простаивающим?
10. В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Постройте ряд распределения, найдите математическое ожидание и дисперсию случайной величины Х - количества нестандартных деталей среди отобранных.
Вариант 7
1. Вычислите пределы функций:
а) 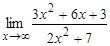 ; б)
; б) 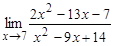 ; в)
; в) 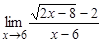 ; г)
; г) 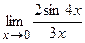 ; д)
; д) 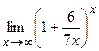 .
.
2. Найдите производные функций. В пункте а) найдите производную третьего порядка:
а) f(x)= 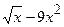 -3; б) f(x)=lnx2×(x6-1) ; в) j(x)=
-3; б) f(x)=lnx2×(x6-1) ; в) j(x)= 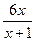 ; г) y=arcsin(3x-1).
; г) y=arcsin(3x-1).
3. Найдите неопределенные интегралы и вычислите определенный интеграл:
а) 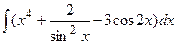 ; б)
; б) 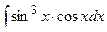 ; в)
; в) 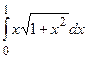 .
.
4. Вычислите площадь фигуры, ограниченной указанными линиями. Сделайте чертеж.
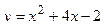 ;
; 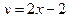 .
.
5. Решите указанные дифференциальные уравнения 1-го и 2-го порядков
а) 2ydx=(1+x)dy;
б) у¢¢-y=0, найдите частное решение, если у=0, у´=1 при х=0.
6. Для множеств U=Z, А={ 1, 3, 5, 6} и B={-1, 1, 2, 3} найдите: а) АÈВ, б) АÇВ, в) А \ В, г) 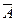 , д) АDВ.
, д) АDВ.
7. а) Разложите в степенной ряд по степеням х функцию y= ln(1+5x);
б) Вычислите приближенно с точностью до 0,0001 значение выражения cos20°.
8. Вычислите силу тока I (A) в однородном участке цепи с напряжением U=140±0,5 (В) при постоянном сопротивлении участка R=70±0,6 (Ом). Найдите абсолютную DI и относительную eI погрешности.
9. Транзисторный приемник смонтирован на 9 полупроводниках, для которых вероятность брака равна 0,05. Найдите вероятность того, что радиоприемник будет неработоспособным, если он отказывает при наличии в нем не менее одного бракованного полупроводника.
10. Среди 10 агрегатов 4 нуждаются в дополнительной смазке. Составьте закон распределения и найдите математическое ожидание и дисперсию числа агрегатов, нуждающихся в дополнительной смазке, среди трех, наудачу отобранных из общего числа.
Вариант 8
1. Вычислите пределы функций:
а) 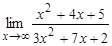 ; б)
; б) 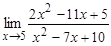 ; в)
; в) 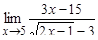 ; г)
; г) 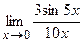 ; д)
; д) 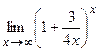 .
.
2. Найдите производные функций. В пункте а) найдите производную третьего порядка:
а) f(x)=6 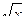 +
+ 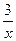 -x2; б) y=(e2x-4)
-x2; б) y=(e2x-4) 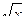 ; в) f(x)=
; в) f(x)= 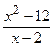 ; г) y=arccos(
; г) y=arccos( 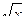 ).
).
3. Найдите неопределенные интегралы и вычислите определенный интеграл:
а) 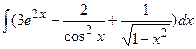 ; б)
; б) 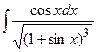 ; в)
; в) 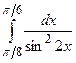 .
.
4. Вычислите площадь фигуры, ограниченной указанными линиями. Сделайте чертеж.
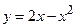 ;
; 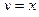 .
.
5. Решите указанные дифференциальные уравнения 1-го и 2-го порядков
а) ydx-dx+xdy=0;
б) у¢¢+2у´-8y=0, найдите частное решение, если у=4, у´=-4 при х=0.
6. Для множеств U=Z, А={ -4, 1, 2, 3} и B={0, 1, 3, 4} найдите: а) АÈВ, б) АÇВ, в) А \ В, г) 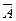 , д) АDВ.
, д) АDВ.
7. а) Разложите в степенной ряд по степеням х функцию y=xex;
б) Вычислите приближенно с точностью до 0,0001 значение выражения 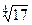 .
.
8. Вычислите силу тока I (A) в однородном участке цепи с напряжением U=190±0,5 (В) при постоянном сопротивлении участка R=20±0,6 (Ом). Найдите абсолютную DI и относительную eI погрешности.
9. По четырем каналам передаётся одинаковое сообщение. Вероятности того, что из-за помехи прием будет неправильным, неодинаковы и соответственно равны: Р1 = 0,2; Р2 = 0,3; Р3 = 0,25; Р4 = 0,35. Найдите вероятность того, что не менее чем по одному каналу сообщение будет принято правильно.
10. Три из семи одинаковых по внешнему виду радиоламп неисправны. Наугад выбирают 4 лампы и проверяют на испытательном стенде. Постройте ряд распределения случайной величины Х - числа радиоламп, которые будут работать. Найдите математическое ожидание и дисперсию.
Вариант 9
1. Вычислите пределы функций:
а) 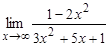 ; б)
; б) 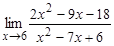 ; в)
; в) 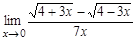 ; г)
; г) 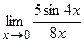 ; д)
; д) 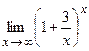 .
.
2. Найдите производные функций. В пункте а) найдите производную третьего порядка:
а) f(x)=x7+2x5+ 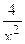 -1; б) f(x)=
-1; б) f(x)= 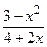 ; в) f(x)=ctgx×lnx2; г) y=arcсtg(x3).
; в) f(x)=ctgx×lnx2; г) y=arcсtg(x3).
3. Найдите неопределенные интегралы и вычислите определенный интеграл:
а) 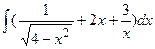 ; б)
; б) 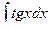 ; в)
; в) 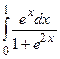 .
.
4. Вычислите площадь фигуры, ограниченной указанными линиями. Сделайте чертеж.
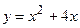 ;
; 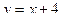 .
.
5. Решите указанные дифференциальные уравнения 1-го и 2-го порядков
а) y´=5x3-sinx;
б) у¢¢-22у¢+121у=0, найдите частное решение, если у=1, у´=-2 при х=0.
6. Для множеств U=Z, А={ -5, -1, 3, 5} и B={-3, 1, 3, 4} найдите: а) АÈВ, б) АÇВ, в) А \ В, г) 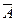 , д) АDВ.
, д) АDВ.
7. а) Разложите в степенной ряд по степеням х функцию y= 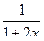 ;
;
б) Вычислите приближенно с точностью до 0,0001 значение выражения sin10°.
8. Вычислите силу тока I (A) в однородном участке цепи с напряжением U (В) при постоянном сопротивлении участка R (Ом). Найдите абсолютную DI и относительную eI погрешности. U=200±0,5, R=50±0,6.
9. Мастер обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания рабочего 0,3, второй – 0,6, третий – 0,4, четвёртый – 0,25. Найдите вероятность того, что в течение смены хотя бы один станок не потребует внимания рабочего.
10. Среди 10 изготовленных приборов 3 неточных. Составьте закон распределения числа неточных приборов среди взятых наудачу четырёх приборов. Найдите математическое ожидание и дисперсию этой случайной величины.
Вариант 10
1. Вычислите пределы функций:
а) 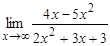 ; б)
; б) 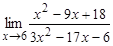 ; в)
; в) 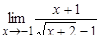 ; г)
; г) 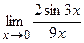 ; д)
; д) 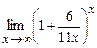 .
.
2. Найдите производные функций. В пункте а) найдите производную третьего порядка:
а) f(x)=x9-3x5 - 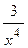 +2; б) f(x)=
+2; б) f(x)= 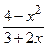 ; в) f(x)=x×tglnx; г)
; в) f(x)=x×tglnx; г) 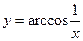 .
.
3. Найдите неопределенные интегралы и вычислите определенный интеграл:
а) 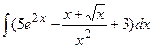 ; б)
; б) 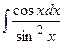 ; в)
; в) 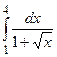 .
.
4. Вычислите площадь фигуры, ограниченной указанными линиями. Сделайте чертеж.
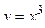 ;
; 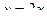 .
.
5. Решите указанные дифференциальные уравнения 1-го и 2-го порядков
а) (1+х2)dу=3x2 уdх;
б) у¢¢+49у=0, найдите частное решение, если у=0, у´=1 при х=0.
6. Для множеств U=Z, А и B найдите: а) АÈВ, б) АÇВ, в) А \ В, г) 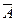 , д) АDВ.
, д) АDВ.
А={ -10, -6, -5, -4}, B={-5, -4, 0}.
7. а) Разложите в степенной ряд по степеням х функцию у= 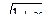 ;
;
б) Вычислите приближенно с точностью до 0,0001 значение выражения ln0,7.
8. Вычислите силу тока I (A) в однородном участке цепи с напряжением U=220±0,5 (В) при постоянном сопротивлении участка R=80±0,6 (Ом). Найдите абсолютную DI и относительную eI погрешности.
9. Сборщик получает 45% деталей завода № 1, 30% - завода № 2, 25% - завода № 3. Вероятность того, что деталь первого завода отличного качества равна 0,7, для деталей второго и третьего заводов эти вероятности соответственно равны 0,8 и 0,9. Найдите вероятность того, что наудачу взятая сборщиком деталь оказалась отличного качества.
10. Среди 10 изготовленных приборов 3 неточных. Составьте закон распределения числа неточных приборов среди взятых наудачу 5 приборов. Найдите математическое ожидание и дисперсию этой случайной величины.
Вопросы к зачету
1. Функции одной независимой переменной и её свойства.
2. Предел функции в точке и его свойства.
3. Односторонние пределы. Условия существования предела функции.
4. Предел функции на бесконечности. Замечательные пределы. Число е.
5. Непрерывность функции в точке и на отрезке. Классификация точек разрыва.
6. Определение производной. Физический и геометрический смысл производной.
7. Основные правила дифференцирования. Таблица производных.
8. Производная сложной функции. Производные высших порядков.
9. Исследование функции на экстремумы и промежутки монотонности.
10. Применение производной при исследовании функции на выпуклость и точки перегиба.
11. Первообразная и неопределённый интеграл. Основные свойства неопределённого интеграла.
12. Таблица неопределённых интегралов.
13. Вычисление неопределённых интегралов методом интегрирования по частям и методом введения новой переменной.
14. Определённый интеграл и его геометрическое истолкование. Основные свойства определённого интеграла.
15. Формулы площади и объема цилиндра, призмы; площади их поперечных сечений.
16. Вычисление определённого интеграла методом замены переменной и по частям.
17. Дифференциальные уравнения, общие понятия. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения.
18. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
19. Определение числового ряда. Степенные ряды. Знакопеременные числовые ряды.
20. Разложение функции в ряд Тейлора и Маклорена.
21. Основные понятия теории множеств. Задание множеств. Операции над множествами.
22. Отношения. Свойства отношений.
23. Основные понятия теории графов.
24. Абсолютная и относительная погрешности. Округление чисел.
25. Погрешности простейших арифметических действий.
26. Понятие события и вероятности события. Достоверные и невозможные события. Классическое определение вероятностей.
27. Основные понятия теории вероятностей.
28. Теоремы теории вероятностей.
29. Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения случайной величины.
30. Математическое ожидание случайной величины. Дисперсия случайной величины. Среднее квадратичное отклонение случайной величины.
СОДЕРЖАНИЕ
| Введение …………………………………………………………………………...... 1. Объем учебной дисциплины и виды учебной работы ………………………… 2. Тематический план ………………………………………………………………. 3. Литература ………………………………………………………………………... 4. Программа, методические указания и вопросы для самоконтроля…................ 4.1 Раздел 1. Математический анализ……………………………………………… 4.2 Раздел 2. Ряды …………………………………………………………………... 4.3 Раздел 3. Основы дискретной математики ……………………………………. 4.4 Раздел 4. Численные методы …………………………………………………... 4.5 Раздел 5. Основы теории вероятностей и математической статистики …….. 5. Варианты контрольной работы …………………………………………………. 6. Вопросы к зачету ………………………………………………………………… | 4 6 8 9 10 10 28 32 33 36 47 57 |
Введение
Настоящие методические указания составлены в соответствии с рабочей программой по дисциплине «Математика» для студентов специальности 08.02.08 Монтаж и эксплуатация оборудования и систем газоснабжения. Программа предназначена для реализации требований ФГОС к минимуму содержания и уровню подготовки выпускников по данной специальности среднего профессионального образования и является единой для всех форм обучения.
Формой обучения студента заочного отделения является самостоятельная работа над учебным материалом, которая состоит их следующих элементов: изучение материала по учебникам, решение задач, самопроверка, выполнение контрольных работ. В процессе самостоятельной работы студент может обращаться к преподавателю с вопросами для получения письменной или устной консультации. В помощь студентам заочного отделения организуются чтение лекций, практические занятия. Завершающим этапом изучения отдельных частей курса «Математика» является зачёт в соответствии с учебным планом по специальности.
Изучение материала по учебнику
Изучение материала по учебнику следует выполнять согласно указанным в программе курса темам. Изучая тот или иной вопрос темы по учебнику, целесообразно выполнять на бумаге все вычисления и вычерчивать имеющиеся в учебнике чертежи.
При самостоятельном изучении материала полезно вести конспект. В конспект по мере проработки материала рекомендуется вписывать определения, теоремы, формулы, уравнения и т.п. Поля конспектов могут послужить для выделения тех вопросов, на которые необходимо получить письменную или устную консультации. Ведение конспекта должно быть аккуратным, расположение текста хорошо продуманным.
Самопроверка
Опыт прочного усвоения материала темы показывает, что самопроверку проводить необходимо. В настоящем пособии приводятся для самопроверки вопросы, которые акцентируют внимание на наиболее важных, ключевых положениях темы. В процессе выполнения самопроверки необходимо избегать пользования учебником или конспектом. Желание обратиться к учебнику или конспекту показывает недостаточное усвоение материала темы.
Консультации
При изучении теоретического материала или при решении задач у студента могут возникнуть вопросы, разрешить которые самостоятельно не удается. В такой ситуации студенту следует обратиться к преподавателю для получения от него письменной или устной консультации. При этом необходимо точно указать вопрос, учебник и место в учебнике, где рассмотрен затрудняющий студента вопрос. Если непреодолимые затруднения возникли при решении задачи, то следует указать характер затруднения, привести план решения.
Контрольная работа
В процессе изучения курса студент должен выполнить одну контрольную работу, которая проходит рецензирование. По полученным результатам студент может сделать выводы о степени усвоения им соответствующего раздела курса, внести коррективы в процесс последующей самостоятельной работы по изучению теоретического материала.
К выполнению контрольной работы следует приступать после тщательного разбора имеющихся в учебнике и сборниках задач решений с ответами. В дополнение к предложенным задачам сборников в данном пособии рассмотрены некоторые примеры.
Контрольные работы должны выполняться самостоятельно, так как в противном случае рецензирование работы как диалог общения преподавателя – рецензента и студента с целью оказания последнему методической помощи не достигнет цели.
Контрольную работу следует выполнять в отдельной 12-листовой тетради, на внешней обложке указать фамилию, имя, отчество, курс, группа, вариант контрольной работы (образец взять у секретаря на отделении).
Выбор варианта зависит от номера в списке учебного журнала (определяется по последней цифре, например, №25 – вариант №5)
Работа выполняется чёрными, синими или фиолетовыми чернилами с полями для замечаний рецензента.
Решения задач должны быть подробными, без сокращения слов. Перед решением каждой задачи должно присутствовать условие – формулировка задания или задачи. Задачи располагать в порядке номеров, указанных в задании, не меняя этих номеров.
Чертежи можно выполнять от руки, но аккуратно.
Выполненная работа сдаётся секретарю отделения для регистрации и последующей проверки преподавателем.
Работу следует сдавать не менее чем за 2 недели до зачёта.
Если работа выполнена с ошибками, либо не в полном объёме, контрольная работа возвращается студенту с подробными замечаниями для доработки, при этом работа над ошибками выполняется в той же тетради.
Контрольная работа, выполненная небрежно, неразборчивым почерком, без соблюдения требований по оформлению возвращается студенту без проверки с указанием причин возврата на титульном листе.
Студент допускается к сдаче зачета при положительной аттестации контрольной работы.
Зачеты и экзамены
К зачету допускаются студенты, выполнившие контрольную работу (работы должны быть зачтены преподавателем-рецензентом). Определения, теоремы, правила должны формулироваться точно и с пониманием существа дела: решение задач должно выполняться без ошибок и уверенно. Только при выполнении этих условий знания студента могут быть признаны удовлетворяющими требованиям, предъявленными программой.
Цели и задачи учебной дисциплины – требования к результатам освоения учебной дисциплины «Математика»
В результате освоения учебной дисциплины обучающийся должен уметь:
- находить производные;
- вычислять неопределённые и определённые интегралы;
- решать прикладные задачи с использованием элементов – дифференциального и интегрального исчислений;
- решать простейшие дифференциальные уравнения;
- находить значения функций с помощью ряда Маклорена.
В результате освоения учебной дисциплины обучающийся должен знать:
- основные понятия и методы математического анализа, дискретной математики;
- основные численные методы решения прикладных задач;
- основные понятия теории вероятностей и математической статистики.
Изучение дисциплины «Математика» способствует формированию следующих общих и профессиональных компетенций:
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.
ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии для совершенствования профессиональной деятельности.
ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Ставить цели, мотивировать деятельность подчиненных, организовывать и контролировать их работу с принятием на себя ответственности за результат выполнения заданий.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Быть готовым к смене технологий в профессиональной деятельности.
ПК 1.1. Конструировать системы газораспределения и газопотребления.
ПК 1.2. Выполнять расчеты систем газораспределения и газопотребления.
ПК 1.3. Составлять спецификацию материалов и оборудования на системы газораспределения и газопотребления.
ПК 1.4. Осуществлять руководство другими работниками в рамках подразделения и взаимодействие с сотрудниками смежных подразделений при выполнении работ по проектированию газораспределения и газопотребления.
ПК 2.1. Организовывать и выполнять подготовку систем и объектов к строительству и монтажу.
ПК 2.2. Организовывать и выполнять работы по строительству и монтажу систем газораспределения и газопотребления.
ПК 2.3. Организовывать и выполнять производственный контроль качества строительно-монтажных работ.
ПК 2.4. Выполнять пусконаладочные работы систем газораспределения и газопотребления.
ПК 2.5. Руководство другими работниками в рамках подразделения и взаимодействие с сотрудниками смежных подразделений при выполнении работ по строительству и монтажу систем газораспределения и газопотребления.
ПК 3.1. Осуществлять контроль и диагностику параметров эксплуатационной пригодности систем газораспределения и газопотребления.
ПК 3.2. Осуществлять планирование работ, связанных с эксплуатацией и ремонтом систем газораспределения и газопотребления.
ПК 3.3. Организовывать производство работ по эксплуатации и ремонту систем газораспределения и газопотребления.
ПК 3.4. Организовывать производство работ по реконструкции систем газораспределения и газопотребления.
ПК 3.5. Осуществлять надзор и контроль за ремонтом и его качеством.
1. Объем учебной дисциплины и виды учебной работы
| Вид учебной работы | Объем часов |
| Максимальная учебная нагрузка (всего) | 96 |
| Обязательная аудиторная учебная нагрузка (всего) | 12 |
| в том числе: | |
| практические занятия | 10 |
| Самостоятельная работа обучающегося (всего) | 84 |
| в том числе: | |
| выполнение упражнений и задач по темам; работа с текстом конспекта, дополнительной литературы, выполнение домашней контрольной работы | 84 |
| Промежуточная аттестация в форме дифференцированного зачета | |
2. Тематический план
|
|
Наименование разделов и тем
Всего часов по учебному плану
Количество аудиторных часов при заочной форме обучения
Литература
Основные источники:
1. Григорьев С.Г., С.В. Иволгина, Математика. Учебник для ссузов – М.: Академия, 2011. - 416с.
2. Пехлецкий И. Д. Математика: учеб. для сред. проф. образования / И. Д. Пехлецкий. - 8-е изд., стер. - М. : Академия, 2011. - 304с.
3. Самойленко П.И., Богомолов Н.В. Математика: учебник для ссузов - М.: Дрофа, 2008.
Дополнительные источники:
4. Богомолов, Н. В. Практические занятия по математике : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2015. — 495 с.
5. Данко П.Е., Попов А.Г., Кожевников Г.Я. Высшая математика в упражнениях и задачах. т.I,II - М.: Высшая школа, 2008
6. Спирина, М. С. Теория вероятностей и математическая статистика: учеб. для сред.проф.образования / М. С. Спирина. - 2-е изд., стер. - М. : Академия, 2011. - 352с.
4. Программа, методические указания, вопросы для самоконтроля
Дата: 2018-12-21, просмотров: 590.