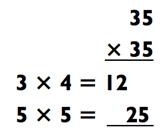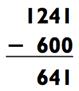Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Вот ещё один трюк.

Как вы, возможно, знаете, квадрат числа - это заданное число, умноженное само на себя. Например, квадратом 7 будет 7 х 7 = 49. Позже я научу вас простому способу, который позволит вам легко вычислять квадрат любого двузначного или трёхзначного (и даже больше) числа. Этот метод особенно просто применять, когда число заканчивается на 5. Так что давайте опробуем данный приём уже сейчас.

1) Полученный ответ должен начинаться с результата умножения первой цифры возводимого в квадрат числа на следующую после неё в иерархии

2) Полученный ответ заканчивается на 25.

 

 

Например, чтобы возвести в квадрат число 35, мы просто умножаем первую цифру (3) на следующую после неё в иерархии (4), после чего добавляем 25. Так как 3 х 4 = 12, ответ будет 1225. Таким образом, 35 х 35 = 1225. Проделанные шаги могут быть представлены следующим образом:

 

 

 

Как на счёт возведения в квадрат числа 85? Так как 8 х 9 = 72,

мы мгновенно получаем 85 х 85 = 7225:

 

 

 

 

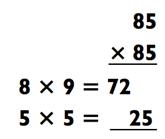
Мы можем использовать схожий приём, когда умножаем двузначные числа с одинаковыми первыми цифрами, и с дающими в

сумме 10 вторыми цифрами. Полученный ответ начинается с цифры, полученной с помощью вышеописанного метода (первая цифра умноженная на следующую после неё в иерархии), далее идет произведение вторых цифр, участвующих в умножении чисел. Например, попробуем 83 х 87. (оба числа начинаются на 8, а их последние цифры в сумме 3 + 7 = 10) Так как 8 х 9 = 72, и 3 х 7 = 21,

ответ будет 7221.

 

 

 

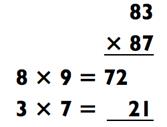
Схожим образом получаем и 84 х 86 = 7224.

Теперь ваша очередь. Попробуйте.

26 х 24

С чего начинается ответ? С 2 х 3 = 6. На что заканчивается? На

6 х 4 = 24. Соответственно, 26 х 24 = 624.

Помните, что использовать данный метод можно только когда первые цифры чисел одинаковы, а последние дают в сумме 10. Итак, мы можем его использовать, чтобы мгновенно определить:

 

 

 

 

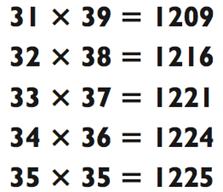
Вы можете спросить:

 

 

«Что если последние цифры не дают в сумме 10? Мы всё равно можем использовать данный приём, чтобы

Посчитать 22 х 23?»

Пока ещё нет. Но в Главе 8, я покажу вам простой способ для решения таких задач с использованием метода «совместной близости» (для действия 22 х 23 вы будете использовать 20 х 25 плюс 2 х 3 и получите 500 + 6 = 506; но это я забегаю вперёд!). Вы не только научитесь использовать данные методы, но вы также сможете понять принципы их работы.

 

«Существуют какие-либо методы устного сложения и

Вычитания?»

Определённо: и об этом вся следующая глава. Если бы меня принудили описать свой метод в двух словах, я бы сказал: «Слева направо».  Вот вы украдкой и получили анонс.

Представьте себе следующую задачу на вычитание:

 

 

 

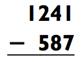
Большинству  людей  не  понравится  решать  эту  задачку  в  уме

(или даже на бумаге!), но давайте всё упростим. Вместо того, чтобы

вычесть  587,  вычтем  600.  Так  как  1200  -  600  =  600,  мы  получаем следующее:

 

 

Но мы вычли на 13 больше. (в Главе 3 будет объяснено, как быстро определить «13») Таким образом, наш пример, на который было больно смотреть, превращается в легкую задачу на сложение,

 

 

 

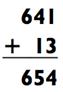
которую совсем просто решить в уме (в особенности слева направо). Итак, 1241 - 587 = 654.

Используя немножко математемагии, описанной в Главе 9, вы сможете мгновенно вычислять сумму десяти чисел, представленных ниже:

Хотя я не буду раскрывать магический секрет прямо сейчас, вот небольшой намёк. Полученный ответ, 935, уже появлялся в рамках данной главы. Ещё больше трюков для вычислений на бумаге вы найдёте в Главе 6. Более того, вы будете в состоянии быстро назвать частное двух следующих чисел:

 

 

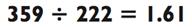
( первые три цифры )

Нам ещё много предстоит обсудить касательно деления

(включая обычные и десятичные дроби) в Главе 4.