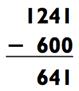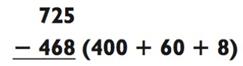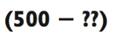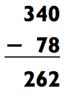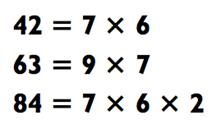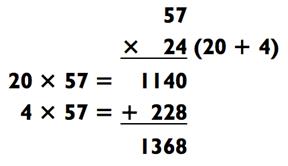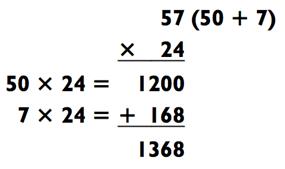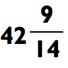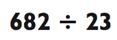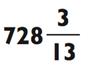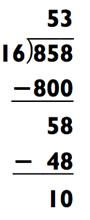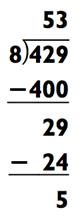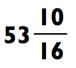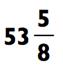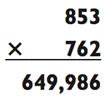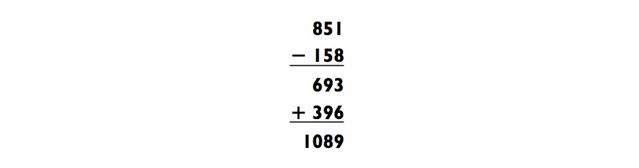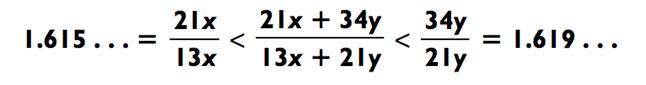СЕКРЕТЫ МЕНТАЛЬНОЙ МАТЕМАТИКИ
|
|
Мгновенное умножение
Давайте начнём с одного из моих любимых подвигов устной математики: как умножать в уме любое двузначное число на 11. Это очень легко, если вы знаете секрет.
Представьте следую задачу:
Х 11
Для решения данной задачи нужно просто сложить цифры, 3 + 2
= 5, а затем поместить 5-ку между 2-ой и 3-ой. Вот и ваше решение:
352
Что может быть легче? Теперь попробуйте:
Х 11
С тех пор, как 5 + 3 = 8, ответ достаточно простой:
583
Ещё пример. Не подглядывая и ничего не записывая, чему будет равно:
Х 11?
У вас получилось 891? Поздравляю!
Пока вы ещё не через чур воодушевились: я показал вам лишь половину того, что необходимо знать. Допустим задача следующая:
Х 11
Несмотря на то, что 8 + 5 = 13, ответ НЕ 8135!
Как и прежде, цифра 3 ставится между, но 1 добавляется к цифре 8 для получения правильного ответа: 935
Представляйте задачу следующим образом:
Вот ещё пример. Попробуйте 57 х 11.
Так как 5 + 7 = 12, решением будет:
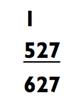
Так, теперь ваша очередь. Как можно быстрее, сколько будет
77 х 11?
Если вы получили ответ 847, то можете похлопать себя по спине.
Вы на пути к превращению в матемага.
Я знаю по опыту, что если вы скажете другу или учителю, что можете в уме умножить любое двузначное число на 11, просьба умножить 99 на 11 не заставит себя долго ждать. Так давайте сделаем это прямо сейчас, чтобы вы были готовы.
Раз уж 9 + 9 = 18, то ответ:
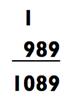
Хорошо попрактикуйте свой новый навык какое-то время, а затем начинайте выпендриваться. Вы будете удивлены тому, какую реакцию это вызовет. (раскрывать или нет свои секреты - решайте сами!)
Добро пожаловать назад. К этому моменту у вас, должно быть, появилось несколько вопросов, таких как:
«Можем ли мы использовать данный метод для умножения трёхзначных (или больше) чисел на 11?»
Безусловно. Например, для задачки 314 х 11 ответ всё ещё будет начинаться с 3 и заканчиваться на 4. Так как 3 +1 = 4, а 1 + 4 = 5, ответ будет 3454. Но мы отложим задачи посерьёзнее напотом.
Вероятнее всего, вы должно быть спрашиваете себя:
«Ну, это хорошо, что можно умножать на 11. Но как на счёт больших цифр? Как умножить цисла на 12, 13 или 36?»
Мой ответ на это: ТЕРПЕНИЕ! Об этом рассказано дальше в книге. В главах 2, 3, 6 и 8 вы изучите методы умножения, позволяющие перемножать любые 2 числа. А ещё лучше то, что вам не придётся запоминать специальные правила для каждого случая. Пригоршня методов - вот всё, что вам понадобится для умножения чисел в уме быстро и с лёгкостью.
Посчитать 22 х 23?»
Пока ещё нет. Но в Главе 8, я покажу вам простой способ для решения таких задач с использованием метода «совместной близости» (для действия 22 х 23 вы будете использовать 20 х 25 плюс 2 х 3 и получите 500 + 6 = 506; но это я забегаю вперёд!). Вы не только научитесь использовать данные методы, но вы также сможете понять принципы их работы.
«Существуют какие-либо методы устного сложения и
Вычитания?»
Определённо: и об этом вся следующая глава. Если бы меня принудили описать свой метод в двух словах, я бы сказал: «Слева направо». Вот вы украдкой и получили анонс.
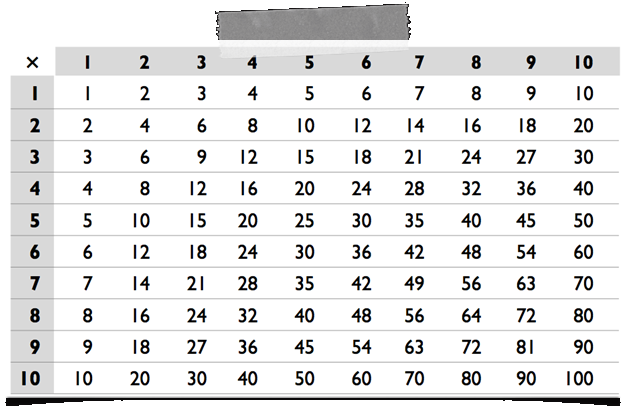
Представьте себе следующую задачу на вычитание:
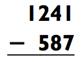
Большинству людей не понравится решать эту задачку в уме
(или даже на бумаге!), но давайте всё упростим. Вместо того, чтобы
|
Но мы вычли на 13 больше. (в Главе 3 будет объяснено, как быстро определить «13») Таким образом, наш пример, на который было больно смотреть, превращается в легкую задачу на сложение,
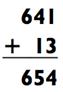
которую совсем просто решить в уме (в особенности слева направо). Итак, 1241 - 587 = 654.
|
Хотя я не буду раскрывать магический секрет прямо сейчас, вот небольшой намёк. Полученный ответ, 935, уже появлялся в рамках данной главы. Ещё больше трюков для вычислений на бумаге вы найдёте в Главе 6. Более того, вы будете в состоянии быстро назвать частное двух следующих чисел:
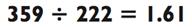
( первые три цифры )
Нам ещё много предстоит обсудить касательно деления
(включая обычные и десятичные дроби) в Главе 4.
Улучшайте свою память
В Главе 7 вы изучите полезную технику для запоминания чисел. Это окажется полезным внутри класса и за его пределами. Используя легкую для понимания систему трансформации цисел в слова, вы сможете быстро и без труда запоминать любые числа: даты, телефонные номера - всё, что захотите.
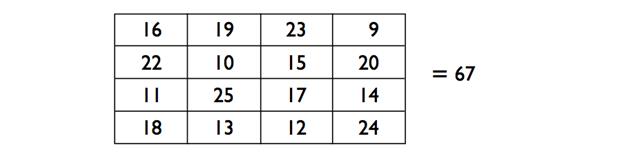
Говоря о календарных числах, как вы смотрите на то, чтобы иметь возможность определять день недели за любую дату? Вы можете использовать это для определения дней рождения, исторических событий, запланированных в будущем встреч, и так далее. Я расскажу вам об этом в деталях позже, но вот простой способ определения дня недели 1-го Января любого года в 21-ом веке. Первым делом ознакомьтесь с представленной таблицой:
| ПОНЕДЕЛЬНИК | ВТОРНИК | СРЕДА | ЧЕТВЕРГ | ПЯТНИЦА | СУББОТА | ВОСКРЕСЕНИЕ |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 или 0 |
Например, давайте определим день недели от 1/01/2030. Возьмите последние две цифры года и представьте себе, что это ваш счёт в ресторане. (в данном случае ваш счёт $30) Теперь добавьте чаевых на 25%, но излишки в центах оставьте себе. (можете вычислить это, дважды разделив счёт пополам и отбросив всю «мелочь». Половина $30 будет $15. Затем половина $15 это $7,50. Оставив излишки себе, получим чаевые в размере $7. Отсюда получаем, что ваш счёт плюс чаевые составляет $37. Чтобы определить день недели, вычитаем из этой суммы наиболее близкое к ней - но не большее - произведение числа 7 (0, 7, 14, 21, 28, 35, 42, 49, …) и получаем с помощью этого порядковый номер дня. В данном примере, 37 - 35 = 2,
значит 1-ое Января 2030 года приходится на 2-ой день, под названием Вторник:
СЧЁТ: ЧАЕВЫЕ:
Произведение 7-ки:
|
Как на счёт 1 Января 2043 года:
|
Произведение 7-ки:
= ЧЕТВЕРГ
Исключение : если год високосный, уберите $1 из суммы чаевых, посчитанных ранее. Например, для 1/01/2032, 25% от счёта в $32 будут равны $8 чаевых. Избавление от $1 даёт в итоге 32 + 7 = 39. Вычитание наибольшего по отношению к сумме счёта произведение 7 даёт нам 39
- 35 = 4. Итак, 1-ое Января 2032 года приходится на 4-ый день - ЧЕТВЕРГ. За большей информацией, которая позволит вам вычислять день недели за любую историческую дату, обращайтесь к Главе 9. (в действительности, совершенно нормально будет, если вы сначала прочитаете данную главу)
Я знаю, о чём вы сейчас думаете:
«Почему они не учат этому в школе?»
Я боюсь, что существуют вопросы, на которые даже я не знаю ответа. Вы готовы разучить ещё больше волшебной математики? Ну так чего же мы ждём? Поехали!
|
Сложение слева направо
Большинство из нас были обучены проводить письменные вычисления справа налево. И это нормально для вычислений на бумаге. Но если вы хотите считать в уме (даже быстрее, чем если бы вы делали это на бумаге), то существует достаточное количество убедительных аргументов, объясняющих, почему лучше это делать слева направо. В конце концов, вы читаете числовую информацию слева направо, вы произносите числа слева направо, да и это более естественно - думать о числах (и считать их) слева направо. Когда вы вычисляете ответ справа налево, вы тем самым генерируете его в обратном направлении. Это и делает вычисления в голове такими
сложными. Также, если вы хотите прикинуть ответ, то более важно знать, что он «немного за 1200», чем то, что он «заканчивается на 8». Таким образом, работая по методу «слева направо», вы начинаете решение с самых существенных цифр вашей задачи. Если вы привыкли работать на бумаге справа налево, то вам может показаться неестественным подход «слева направо». Но с практикой к вам придёт понимание того, что это самый естественный и эффективный метод для устных вычислений.
С первым набором задач - сложение двузначных чисел - метод
«справа налево» может и не показаться вам таким уж выгодным. Но будьте терпеливы. Если вы будете держаться рядом со мной, то увидите, что единственно лёгкий путь к решению трёхзначных (и более) задач на сложение, всех задач на вычитание и определённо всех на умножение и деление - это метод «слева направо». Чем раньше вы приучите себя вычислять таким способом, тем лучше.
Сложение двузначных чисел
Наше допущение в данной Главе состоит в том, что вы знаете, как складывать и вычитать числа, состоящие из одной цифры. Мы начнём со сложения двузначных чисел, хоть я и подозреваю, что вы уже довольно хорошо можете делать это в уме. Однако, следующие упражнения всё равно являются хорошей практикой, так как навыки сложения двузначных чисел, которые вы приобретёте здесь, понадобятся для более серьёзных задач на сложение, как впрочем и для практически всех задач на умножение в следующих главах. Это всё также иллюстрирует фундаментальный принцип устной арифметики, а именно: «упрощай задачу, разбивая её на меньшие, легче выполнимые части». Это ключ поистине к каждому методу,
который вы изучите в данной книге. Перефразируя старую пословицу, существуют три составляющих успеха - упрощай, упрощай, упрощай2.
Самые легкие задачи на сложение двузначных чисел, это те, которые не требуют от вас держать в уме никакие цифры (то есть когда первые две цифры в сумме дают 9 или меньше, или когда последние две цифры дают в сумме 9 или меньше). Например:
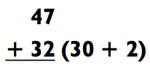
Чтобы посчитать 47 + 32, сначала прибавляем 30, затем 2. После прибавления 30, мы имеем задачу попроще 77 + 2, которая равняется
79. Давайте проиллюстрируем это следующим образом:
Сложение трёхзначных чисел
Стратегия сложения трёхзначных чисел точно такая же, как и для двузначных: вы складываете слева направо. После каждого шага, вы переходите к новой (и более простой) задаче на сложение. Давайте попробуем следующее:
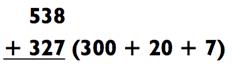
Начиная с 538, мы прибавляем 300, затем 20, затем 7. После
прибавления 300 (538 + 300 = 838), задача сводится к 838 + 27. После
прибавления 20 (838 + 20 = 858), задача упрощается до 858 + 7 = 865. Такого рода мыслительный процесс может быть представлен в виде следующей схемы:
Все задачки на сложение в уме могут быть решены данным способом. Цель состоит в том, чтобы последовательно упрощать задачу до тех пор, пока вам не придётся просто прибавлять однозначное число. Обратите внимание на то, что пример 538 + 327 требует от вас держать в уме шесть цифр, тогда как 838 + 27 и 858 + 7 требуют только пять и четыре, соответственно.
Если вы упрощаете задачу, задача становится легче!
Попробуйте решить следующую задачку на сложение в уме прежде, чем смотреть на наше решение:
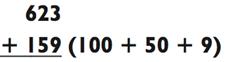
Вы уменьшили и упростили её, прибавляя слева направо? После прибавления сотен (623 + 100 = 723) осталось 723 + 59. Далее вам
следует прибавить десятки (723 + 50 = 773), упростив проблему до 773
+ 9, что вы потом подытоживаете в виде 782. В виде схемы задача выглядит следующим образом:
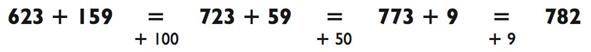
Когда я решаю эти задачи в уме, я не пытаюсь видеть числа у себя в голове - я пытаюсь слышать их. Я слышу пример 623 + 159 как шестьсот двадцать три плюс сто пятьдесят девять; выделяя слово сто для себя, я понимаю, с чего начать. Шесть плюс один равняется семи, значит моя следующая задача семьсот двадцать три плюс пятьдесят девять, и так далее. Когда вы только начинаете решать такие задачи,
делайте это вслух. Подкрепление в виде звуков поможет вам научиться данному методу гораздо быстрее.
Задачи на сложение трёхзначных чисел, на самом деле, не бывают сложнее следующей:
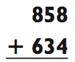
Взгляните на то, как мы это сделали:
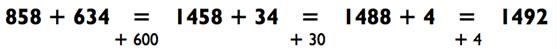
На каждом шаге я слышу (не вижу) новую задачу на сложение. У меня в голове проблема звучит как:
Вычитание слева направо
Для большинства из нас, сложение легче вычитания. Но если вы продолжите вычитать слева направо и разбивать примеры на более простые действия, вычитание может стать почти таким же простым, как сложение.
Вычитание двузначных чисел
В процессе вычитания двузначных чисел вы преследуете цель упростить задачу, доведя её до вычитания (или сложения) однозначного числа. Давайте начнём с очень простого примера на вычитание:
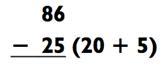
После каждого действия вы прибываете на новый и более лёгкий этап вычитания. Здесь мы сперва отнимаем 20 (86 - 20 = 66),
далее мы отнимаем 5, чтобы достигнуть самого простого действия 66 -
5 для получения итогового ответа 61. Задача может быть схематически представлена как:
СНАЧАЛА ОТНИМАЕМ 30
ЗАТЕМ ПРИБАВЛЯЕМ 1
Вот правило, помогающее решить, какой метод использовать:
если задача на вычитание двузначных чисел требует «заёма», то
округляйте цифру, которую отнимаете. Вычитайте округлённое число, а потом прибавляйте разницу.
Например, задача 54 - 28 требует заёма (так как 8 больше 4),
значит округляем 28 до 30, считаем 54 - 30 = 24, после чего прибавляем
2 и получаем 26 в качестве ответа:
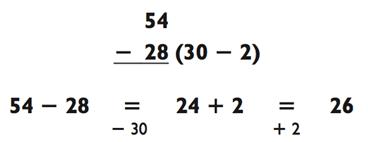
А теперь набейте руку (или голову) на примере 81 - 37. Так как 7 больше 1, мы округляем 37 до 40, вычитаем это число из 81 (81 - 40 = 41), а затем прибавляем назад разницу в виде 3 для получения итогового ответа:
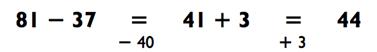
Всего лишь немного практики и вы без труда сможете решать задачи обоими способами. Просто используйте вышеуказанное правило для принятия решения о том, какой способ лучше подходит.
Вычитание трёхзначных чисел
А теперь давайте попробуем вычитание трёхзначных чисел:
Этот конкретный пример не требует от вас занимать никакие числа (так как каждая цифра второго числа как минимум на единицу меньше цифр первого), так что он не должен вам показаться слишком сложным. Просто вычитайте по одной цифре за раз, с каждым шагом упрощая задачу.
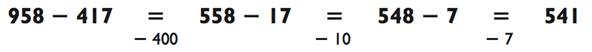
А теперь давайте взглянем на задачку по вычитанию трёхзначных чисел, которая подразумевает заём:
На первый взгляд она, возможно, кажется довольно сложной. Но если вы сначала отнимете 747 - 600 = 147, а потом прибавите назад 2, то получите итоговый ответ 147 + 2 = 149.
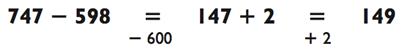
А теперь попробуйте сами:
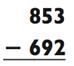
Вы сначала отняли 700 от 853? Если да, то получили ли вы потом 853 - 700 = 153? Так как вы отняли на 8 больше, то добавили ли 8 назад, чтобы получить 161, итоговый ответ?
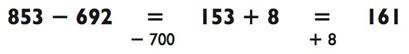
Теперь я могу признать, что нам удалось упростить вашу жизнь путём вычитания чисел, почти кратным 100. (Вы заметили?) Но как на счёт других задач, например:
|
|
Если вы будете вычитать по одной цифре за раз, упрощая каждое действие, то ваша последовательность будет выглядеть так:
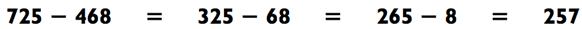
Таблица умножения от 1 до 10
Округление
Вы увидели в прошлой Главе, как полезно может быть округление, когда дело касается вычитания. Та же история и с умножением, особенно когда вы умножаете числа, заканчивающиеся на 8 или 9.
Давайте рассмотрим пример 69 х 6, проиллюстрированный ниже. Слева представлено вычисление обычным способом: прибавляем 360 +
54. Справа, однако, мы округлили 69 до 70 и вычли 420 - 6, что вам может показаться более лёгким действием.
Следующий пример также показывает, насколько легче может быть округление:
Метод вычитания работает особенно хорошо для чисел, которые на одну-две цифры дальше от кратного 10. Он уже не так хорош, когда вам нужно округлять более чем на две цифры, потому что сам пример на вычитание становится сложным. Так что вы можете продолжать придерживаться метода сложения. Лично я, для задач такого размера, использую только метод сложения, потому что за время, потраченное на выбор метода, я бы уже мог всё посчитать!
Раз уж вы можете усовершенствовать свою технику, я настоятельно рекомендую практиковаться побольше на задачках типа
«2-на-1». Ниже представлены 20 примеров, решения на которые вы можете поискать. Я предоставил вам ответы в конце книги, включая разбивку на действия для каждого компонента процесса умножения. Если после разбора каждого из примеров вы захотите ещё попрактиковаться, то просто составьте свои собственные. Считайте в уме, затем проверяйте ответ с калькулятором. Как только вы почувствуете уверенность в том, что можете выполнять такие задачки моментально в уме, вы будете готовы перейти на следующий уровень устных вычислений.
Числа, дающие в сумме 20
Мне данный паттерн представился удивительным. Затем я опробовал числа, дающие в сумме 26, и результаты были похожими. Первым делом я прорешал примеры 132 = 169, затем 12 х 14 = 168, 11 х
15 = 165, 10 х 16 = 160, 9 х 17 = 153, и так далее. Как и прежде,
расстояния этих произведений от 169 равнялись 12, 22, 32, 42, и так далее (смотри таблицу ниже).
На самом деле, существует простое алгебраичиское объяснение данного феномена (смотри «Почему эти приёмы работают»). Но в то время, я не разбирался в алгебре достаточно хорошо, чтобы доказать
постоянство появления данного паттерна, но я провёл достаточное количество экспериментов с подобными примерами, чтобы убедиться в его существовании.
Затем я осознал, что данный шаблон может помочь мне сделать возведение чисел в квадрат намного легче. Предположим, я хотел возвести в квадрат 13. Вместо того, чтобы умножать 13 х 13,
|
Числа, дающие в сумме 26 | Расстояние от 13 | Их произведение | Расстояние их произведения от 169 | |
| 13 | 13 | 0 | 169 | 0 |
| 12 | 14 | 1 | 168 | 1 |
| 11 | 15 | 2 | 165 | 4 |
| 10 | 16 | 3 | 160 | 9 |
| 9 | 17 | 4 | 153 | 16 |
| 8 | 18 | 5 | 144 | 25 |
почему бы не получить приближённый ответ, используя два числа, которые легче перемножить, но которые также дают в сумме 26? Я выбрал 10 х 16 = 160. Чтобы получить итоговый ответ, я просто прибавил 32 = 9 (так как 10 и 16 находятся на расстоянии 3 от 13).
Таким образом, 132 = 160 + 9 = 169. Всё чётко!
Данный метод схематически можно представить так:
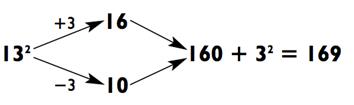
А теперь давайте посмотрим, как это работает с квадратом другого числа:
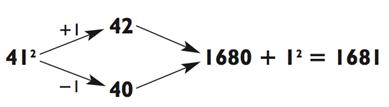
Чтобы возвести в квадрат 41, вычтем 1 для получения 40 и добавим 2 для получения 42. Далее умножаем 40 х 42. Без паники! Это простое умножение типа «2-на-1» под прикрытием (4 х 42, в частности). Так как 4 х 42 = 168, 40 х 42 = 1680. Почти всё! Вам необходимо лишь прибавить квадрат 1 (числа, на величину которого вы уменьшали и увеличивали 41), чтобы получить 1680 + 1 = 1681.
Способно ли возведение в квадрат двузначных чисел быть таким лёгким? Да, с использованием этого метода и небольшим количеством практики, может. И это работает в независимости от того, округляете ли вы исходное число в большую или меньшую сторону.
Например, давайте проверим 772, округлив его во время решения в обе стороны:
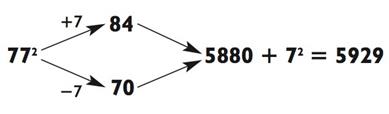
ИЛИ
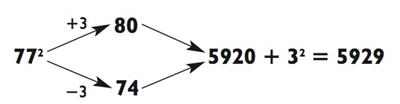
В данном примере преимущество округления в большую сторону состоит в том, что вы практически уже получили решение, осталось лишь просто прибавить 9 к числу с 0 на конце!
По сути, я всегда округляю по принципу большей близости к 10. Так, если возводимое в квадрат число оканчивается на 6, 7, 8, или 9, то округление в большую сторону. И если возводимое в квадрат число оканчивается на 1, 2, 3, или 4, то округление в меньшую сторону. (если число оканчивается на 5, то сразу оба!) Придерживаясь данной стратегии, вы ограничитесь лишь прибавлением чисел 1, 4, 9, 16 или 25 к результатам первой калькуляции.
Давайте рассмотрим другой пример. Вычислите 562 в уме самостоятельно, прежде чем смотреть на наше решение ниже:
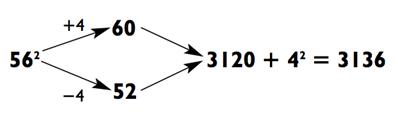
Возведение в квадрат чисел, оканчивающихся на 5 ещё легче. Так как вы каждый раз будете округлять в любую из сторон на величину 5; числа, которые нужно будет перемножить, будут кратны
10. Следовательно, умножение и сложение покажутся особенно простыми. Ниже представлены решения для 852 и 352:
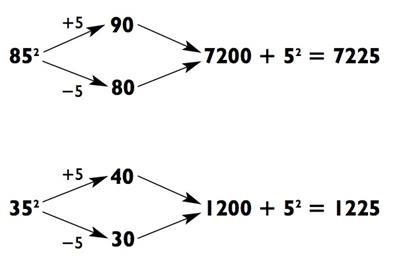
Как вы можете знать из Главы 0, когда происходит возведение в квадрат чисел, оканчивающихся на 5, округление в большую и меньшую стороны позволяет вам немедленно «выпаливать» первую часть ответа, а потом заканчивать его числом 25. Например, когда вы хотите посчитать 752, округление до 80 и 70 даст вам: «пятьсот шестьдесят (пятьдесят шесть сотен) и… двадцать пять!»
Что касается чисел, оканчивающихся на 5, у вас не должно возникнуть проблем с разгромом кого-либо с калькулятором в руке. А после небольшого количества практики с другими примерами на возведение в квадрат, момент, когда вы сможете победить калькулятор в борьбе по возведению в квадрат, не заставит себя долго ждать. Вы даже не испугаетесь больших чисел. Вы можете попросить кого-нибудь загадать вам действительно большое двузначное число, что-нибудь на подобие 90>, и это будет выглядеть, будто вы взяли на себя непосильную задачу.
Но на самом деле это ещё легче, потому что у вас будет возможность округлить до 100.
Давайте представим, что ваша аудитория задала вам 962.
Сначала попробуйте сами, а уже потом смотрите на наше решение:
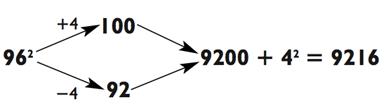
Не было ли это легко? Вам следовало округлить с помощью 4 до 100 и округлить с помощью 4 до 92, а затем умножить 100 х 92 для получения 9200. В этот момент вы можете проговорить вслух: «Девять
тысяч двести (девяносто две сотни)…» и после закончив, используя
«шестнадцать». И наслаждаться аплодисментами.
Одним из первых молниеносных вычислителей, который смог извлечь выгоду из своего таланта был Зера Колберн (1804-1839), сын американского фермера из Вермонта, который выучил таблицу умножения до 100 даже раньше, чем он начал читать и писать. В возрасте шести лет, отец молодого Зеры взял его с собой в тур, где его выступления создали достаточный капитал для того, чтобы отправить его в школу в Париже и Лондоне. В возрасте восьми лет он был известен во всём мире, выступал со своими молниеносными расчётами в Англии и был охарактеризован в Annual Register как
« возможно самый исключительный феномен в истории человеческого разума из когда - либо существующих ». В не меньшей степени Майкл Фарадей и Сэмюэл Морзе восхищались им .
Вне зависимости от того , куда он направлялся , Колберн встречал всех своих соперников со скоростью и точностью . Он рассказывает нам в своей автобиографии о наборе задачек , которые ему задали в Нью - Гемпшире в июне 1811: « Сколько дней и часов прошло с момента рождения Христа 1811 лет назад ? Ответил за двадцать секунд : 661 015 дней , 15 864 360 часов . Сколько секунд содержится в одиннадцати годах ? Ответил за четыре секунды : 346 896 000." Колберн использовал методы , описанные в этой книге , чтобы производить вычисления задчач , которые ему задают , полностью в уме . Например , он бы разложил большое число на более мелкие и затем умножал бы : однажды Колберн умножил 21734 х 543 путём разложения 543 как 181 х 3. Затем он умножил 21734 х 181, чтобы получить 3 933 854, и , наконец , умножил эту цифру на 3, чтобы получить итог в размере 11 801 562.
Как это часто бывает с молниеносными вычислителями , интерес к удивительным способностям Колберна уменьшилась со временем , и в возрасте двадцати он вернулся в Америку и стал проповедником - м е тоди с том . Он у мер в юном возрасте тридцати пяти лет . Подытоживая информацию о своих способностях молниеносного вычи сл ит ел я , и о преимуществах , к оторые та к ая с по с обно с ть предоставляет , Колберн размышлял : « Действительно , метод … тр ебуе т бол ь ше г о к ол ич ес т в а данных , ч е м общее пра в и ло . Н о запомниться то , что ручка , чернила и бумага обходились для Зеры в сумме очень дёшево »
Метод сложения
Чтобы использовать метод сложения для перемножения двух двузначных чисел, вам всего лишь необходимо решить две задачки на умножение типа «2-на-1» и сложить результаты. Например:
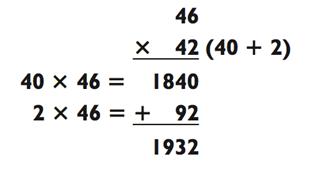
Здесь вы разбиваете 42 на 40 и 2: два числа, на которые легко потом умножать. После вы умножаете 40 х 46, а это всего лишь 4 х 46 с добавочным 0, или 1840. Затем вы умножаете 2 х 46 = 92. Наконец, вы складываете 1840 + 92 = 1932, как и показано выше.
Вот ещё один способ решения той же задачи:
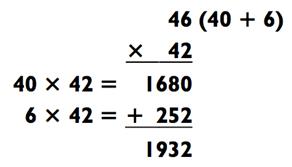
Подвох в том, что умножить 6 х 42 сложнее, чем умножить 2 х 46, как в первой задаче. Более того, прибавить 1680 + 252 сложнее, чем 1840 + 92. Так как определиться с тем, какое из чисел разбить на части? Я стараюсь выбирать число, действия над которым приведут к более простой задаче на сложение. В большинстве случаев, но не всегда, вам будет хотеться разбить число с наименьшей цифрой на конце, потому что это обычно выливается в меньшее число для сложения в будущем.
А сейчас попробуйте свои силы на следующих примерах:
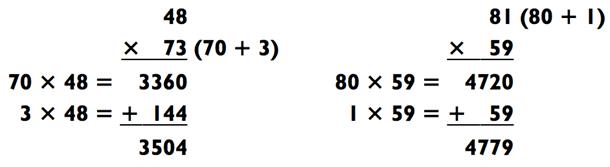
В последнем примере проиллюстрировано то, почему числа с 1 на конце так привлекательны для разбиения. Если оба числа оканчиваются на одинаковую цифру, вам следует делить на части более крупное число, как показано ниже:
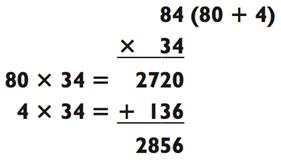
Если одно из чисел на много больше другого, то его разбиение часто оправдывает себя, даже если цифра на конце больше. Вы поймёте, что я имею в виду, когда прорешаете следующие задачи двумя разными способами:
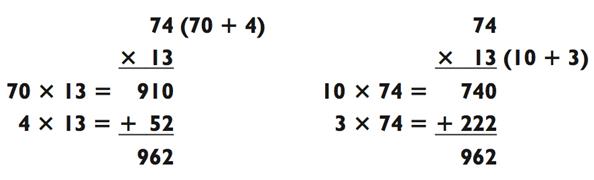
Показался ли вам первый способ быстрее второго? Мне показался. Вот ещё одно исключение из правила «разбивайте на части число с наименьшей цифрой на конце». Когда вы будете умножать число типа 50> на чётное число, вам захочется разбить на части именно число типа 50>:
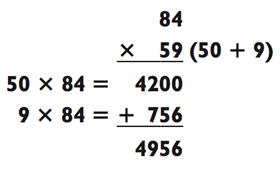
Цифра на конце у числа 84 меньше, чем у числа 59. Но если вы разделите на части 59, результаты умножения будут кратны 100, прямо как 4200 из примера выше. Это делает последующие задачи на сложение многим легче.
А теперь опробуйте лёгкую задачку другого типа:
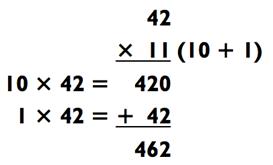
Хотя вычисления, показанные выше, достаточно простые, существует ещё более лёгкий и быстрый способ умножения числа на
11. Это матемагия во всей своей красе: вы не поверите своим глазам, когда увидите это! (если вы, конечно, ещё не забыли про Главу 0)
Вот как это работает. Представьте себе двузначное число, цифры которого в сумме дают 9 или меньше. Для умножения такого числа на 11, просто сложите эти две цифры и вставьте полученную сумму между двух исходных цифр. Например, чтобы умножить 42 х 11, сначала сложите 4 + 2 = 6. Если вы поместите 6 между 4 и 2, то получите 462, что и является решением!
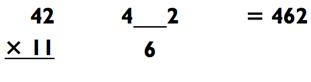
Решите 54 х 11, используя данный метод.
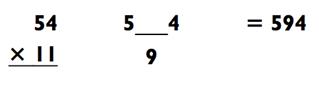
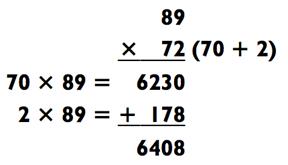
Если вы получили правильный ответ с первого или второго раза, похлопайте себя по спине. В действительности, не найдётся задач на умножение типа «2-на-2» труднее этой. Если вы не получили ответ сразу, не волнуйтесь. В следующих двух разделах я обучу вас гораздо более лёгким стратегиям для решения подобных задач. Но прежде, чем вы продолжите чтение, попрактикуйте метод сложения на следующих задачах на умножение.
Метод вычитания
Метод вычитания действительно может пригодиться, когда одно из умножаемых чисел заканчивается на 8 или 9. Следующий пример иллюстрирует то, что я имею в виду:
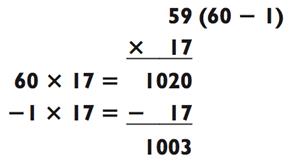
Хотя большинство людей находит сложение легче вычитания, обычно бывает легче отнять маленькое число, нежели прибавить большое. (Если бы мы решали эту задачу методом сложения, то прибавили бы 850 + 153 = 1003)
А теперь давайте возьмёмся за сложную задачу из концовки последнего раздела:
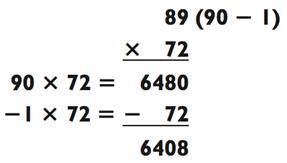
Разве это не намного проще? Теперь задача, где одно из чисел оканчивается на 8:
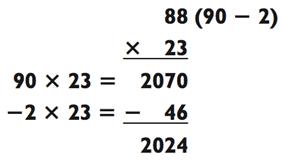
В данном случае вам следует поступить с 88 так: отнимите 90 - 2, затем умножьте 90 х 23 = 2070. Но вы умножили с перебором. Какой перебор? Его размер 2 х 23, или 46. Так что вычтите 46 из 2070 для получения итогового ответа 2024.
Я хочу подчеркнуть, что важным является прорешивание данных примеров в уме, а не просто изучение того, как мы это сделали на схемах. Пропускайте через себя эти задачки, обозначайте действия или даже проговаривайте вслух, дабы подкрепить ваши мысли.
Я использую метод вычитания не только для чисел, оканчивающихся на 8 или 9, но и для чисел типа 90>, потому что 100 является очень удобным числом для умножения. Например, если кто- то попросит меня умножить 96 х 73, я незамедлительно округлю 96 до 100:
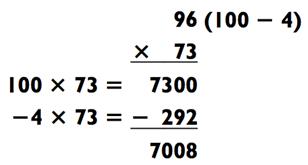
Когда действие на вычитание внутри задачи на умножение требует от вас держать числа в уме, использование дополнений (которые мы изучили в Главе 1) способно помочь вам ускорить получение ответа. Вы поймёте, о чём я говорю, когда поработаете над задачами ниже. Например, вычтите 340 - 78. Нам известно, что ответ будет в районе 200>. Разница между 40 и 78 это 38. Теперь используйте дополнение 38, чтобы получить 62. Это и будет ответ - 262!
|
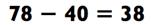
А теперь другая задачка:
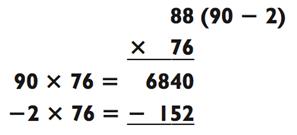
Существует два пути реализации действия на вычитания внутри данной задачи. «Длинный» путь состоит из вычитания 200 и прибавления 48:
Факторинговый метод
Факторинговый метод - мой любимый метод умножения двузначных чисел, так как он совсем не включает в себя ни сложение, ни вычитание. Вы используете его, когда одно из чисел в примере может быть разложено (факторизованно) на числа, состоящие из одной цифры.
Факторизовать число - значит разбить его на «одноцифровые» числа, которые при перемножении дадут исходное число. Например, число 24 может быть фактаризованно в виде 8 х 3 или 6 х 4. (Это также возможно в виде 12 х 2, но мы отдаём предпочтение использованию чисел, состоящих из одной цифры)
Вот несколько других примеров разложенных чисел:
|
|
Для того, чтобы увидет, как факторинг делает умножение легче, рассмотрим следующий пример:
Ранее мы уже решали этот пример путём умножения 46 х 40, 46 х
2 и их последующего сложения. Чтобы использовать метод факторинга, рассмотрим 42 как 7 х 6 и начнём с умножения 46 х 7, что равняется 322. Затем умножим 322 х 6 для получения итогового ответа 1932. Вы уже знаете, как решать задачки на умножение типа
«2-на-1» и «3-на-1», так что это не составит труда:
Конечно, эта задача может быть решена и с перестановкой множителей 42:
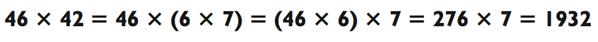
В данном случае легче умножить 322 х 6, чем 276 х 7. Чаще всего я предпочитаю использовать больший множитель при решении исходной задачи типа «2-на-1» и сохраняю меньший множитель для использования его в случае «3-на-1». Следствием факторинга является упрощение задачи на умножение типа «2-на-2» до более лёгкой «3-на-1» (иногда «2-на-1») задачки.
Преимущество метода факторинга для устных вычислений состоит в том, что вам не приходиться слишком многое держать в памяти. Давайте посмотрим на другой пример, 75 х 63:
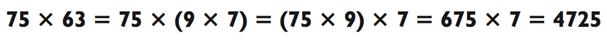
Как и прежде, вы упрощаете этот пример типа «2-на-2» путём разложения 63 на 9 х 7 и затем умножаете 75 на эти числа. (Кстати, причина, по которой мы можем переставить скобки на втором шаге - ассоциативный закон умножения)
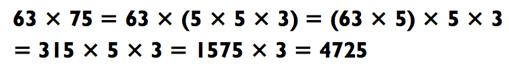
Потренируйтесь на следующем примере:
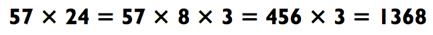
Вы могли бы разложить 24 как 6 х 4 для перехода к другому лёгкому вычислению:
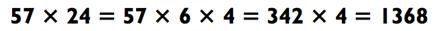
Сравните данный подход с методом сложения:
|
|
В рамках метода сложения, вам необходимо решить две задачи типа «2-на-1», а после сложить результаты. В рамках метода факторинга, перед вами только две задачи на умножение: «2-на-1» и
«3-на-1». И после вы свободны. Метод факторинга обычно снисходителен к вашей памяти.
|
Мы разобрались с этой задачкой достаточно легко, используя метод вычитания, но факторинг работает ещё быстрее:
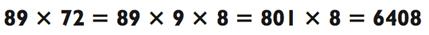
Задача особенно облегчается потому, что в середине 801 находится 0. Наш следующий пример показывает, что иногда разложение чисел с целью воспользоваться ситуацией оправдано. Давайте взглянем на два способа вычисления 67 х 42:
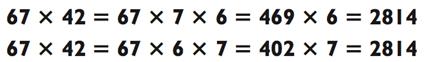
Обычно вам следует разложить 42 как 7 х 6, как в первом примере, и следовать правилу «используй больший множитель в первую очередь». Но задачу легче решить, если вы разложите 42 как 6 х 7, потому что это поспособствует созданию числа с 0 по середине, а это облегчит умножение. Я называю такие числа «дружелюбные произведения».
Ниже, поиски дружелюбного произведения в задаче проведены двумя способами:
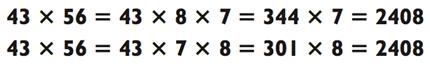
Не показался ли вам второй способ легче?
Во время использования метода факторинга, будет выгодым отыскать дружелюбное произведение где только можно. Следующий список должен помочь. Я жду от вас не столько его запоминания, как простого ознакомления с ним. С практикой вы научитесь чуять дружелюбные произведения, и этот список станет более значимым.
Что за дверью номер 1?
Математическая банальность 1991 года, которая сделала всех вне себя от ярости, была статьёй Мэрилин Вос Савант (женщина, зарегистрированная Книгой Рекордов Гиннесса как человек с самым высоким в мире IQ) в журнале
«Parade». Данный парадокс стали известен как « проблема Монти Холла », и он выглядит следующим образом .
Вы участник « Давайте совершать сделки » (Let’s Make a Deal). Монти Холл даёт вам возможность выбрать одну из трёх дверей : за одной из этих дверей большой приз , за двумя другими - козы . Вы выбираете Дверь № 2. Но прежде чем Монти показывает приз , который вы выбрали , он показывает вам то , что вы не выбрали за Дверью № 3. Это коза . Теперь , в своей дразнящей манере , Монти предоставляет вам другой выбор : вы хотите продолжить с Дверью № 2 или вымхотите рискнуть шансом увидеть , что находится за дверью № 1? Что вам следует сделать ? Если предположить , что Монти собирается показать место , где отсутствует главный приз , то он все г да будет открывать одну из « утешительных дверей ». Это оставляет нас с двумя дверями : одна с большим призом , а другая с утешением . Сейчас шансы 50-50 для вашего выбора , не так ли ?
Неверно ! Шансы , что вы правильно выбрали в первый раз остаются 1 к 3. Вероятность того , что большой приз стоит за другой двери увеличивается до 2 к 3, потому что вероятности в сумме должны давать 1.
Таким образом , путем изменения дверей , вы удвоите шансы на выигрыш ! ( задача предполагает , что Монти всегда будет давать игроку возможность сделать это , что он всегда будет показывать « невыигрышную » дверь и что , когда ваш первый выбор является правильным , он будет выбирать
« невыигрышную » дверь наугад ) Поразмышляйте об игре с десятью дверями . И после вашего выбора он раскрывает восемь других « невыигрышных » дверей . Здесь ваши инстинкты , скорее всего , подскажут вам поменять дверь . Люди путают эту проблему с вариантами : если Монти Холл не знает , где главный приз , и раскрывает Дверь № 3, которая , как оказалось , содержит козу ( хотя это мог бы быть и приз ), то Дверь № 1 будет иметь 50- ти процентный шанс быть правильной . Данный результат настоль ко противоречит здравому смыслу , что Мэрилин Вос Савант получила груды писем ( многие от ученых и даже математиков ), в которых говорилось , что ей не следовало писать о математике . Все они были неправы .
Возведение в куб
Мы закончим эту главу новым методом для возведения в куб двузначных чисел. (Воскресите в памяти тот факт, что куб числа - это число, умноженное на себя дважды. Например, 5 в кубе - обозначаемое 53 — будет равно 5 х 5 х 5 = 125) Как вы убедитесь сами, это не намного труднее, чем умножение двузначных чисел. Метод основан на алгебраическом наблюдении, которое выявило, что
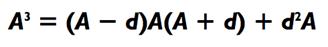
где d - любое число. Как и при возведении в квадрат двузначных чисел, я выбираю в качестве d так, чтобы оно было как можно ближе к кратному десяти. Например, когда возвожу в квадрат 13, то d = 3, а результате чего:
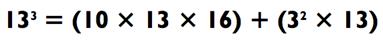
имеем
Так как 13 х 16 = 13 х 4 х 4 = 52 х 4 = 208, и 9 х 13 = 117, то мы
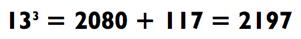
Как на счёт куба 35? Задавая d = 5, мы получаем
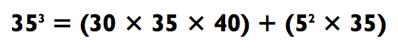
Так как 30 х 35 х 40 = 30 х 1400 = 42 000 и 35 х 5 х 5 = 175 х 5 =
875, мы получаем
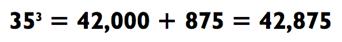
По ходу возведения 49 в куб, мы задаём d = 1 с целью округления до 50. Вот:
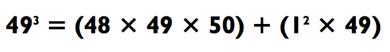
Мы можем решить 48 х 49 с использованием метода факторинга, но для задач такого типа я предпочитаю использовать метод
«совместной близости», который будет описан в Главе 8. (Можете забежать вперёд и взглянуть на него уже сейчас, если хотите!) Используя этот метод, мы получаем 48 х 49 = (50 х 47) + (1 х 2) = 2352. Умножив это число на 50, мы получаем 117 600 и вследствие этого
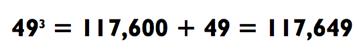
А вот задачка покрупнее. Попробуйте возвести в куб 92.
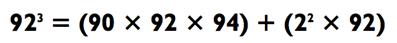
Если вы можете быстро возводить в квадрат двузначные числа, значит вы сможете решить 92 х 94 = 932 - 1 = 8648, или вы могли бы использовать метод «совмесной близости», следствие которого 92 х 94
= (90 х 96) + (2 х 4) = 8648. Умножив это число на 9 (как описано в
начале Главы 8), мы получим 9 х (8600 + 48) = 77 400 + 432 = 77 832, и,
следовательно, 90 х 92 х 94 = 778 320. Так как 4 х 92 = 368, то мы получаем
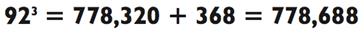
Отметим, что при использовании метода «совместной близости» для задач на умножение, возникающих при возведении в куб трёхзначного числа, малое произведение, которое нужно прибавить (в
зависимоти от того, равняется ли d = 1, 2, 3, 4, или 5), будет 1 х 2 = 2, 2
х 4 = 8, 3 х 6 = 18, 4 х 8 = 32 либо 5 х 10 = 50. Давайте закончим с кубом
96.
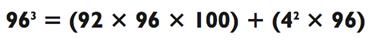
Произведение 92 х 96 = 8832 может быть посчитано множеством разных способов. Дабы отпраздновать окончание данной Главы, давайте используем некоторые из них. Я начну с самого сложного, на мой взгляд, а закончу наилегчайшим. По результатам метода сложения (90 + 2) х 96 = 8640 + 192 = 8832; по результатам метода вычитания 92 х
(100 - 4) = 9200 - 368 = 8832; по результатам метода факторинга 92 х 6 х
4 х 4 = 552 х 4 х 4 = 2208 х 4 = 8832; по результатам возведения в
квадрат 942 - 22 = 8836 - 4 = 8832; по результатам метода совмесной
близости с основой в виде 90, (90 х 98) + (2 х 6) = 8820 + 12 = 8832; и по результатам метода совмесной близости с основой в виде 100, (100 х 88) + (-8 х -4) = 8800 + 32 = 8832.
Произведение 42 х 96 = 1536 может быть так же посчитано несколькими способами, такими как 96 х 4 х 4 = 384 х 4 = 1536 или 16 х (100 -
4) = 1600 - 64 = 1536. И наконец, так как 8832 х 100 = 883 200, мы имеем
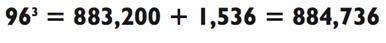
Правило большого пальца
Когда вы делите в уме, а не на бумаге, то вам может показаться сложным запоминание частей ответа, в то время как вы продолжаете вычислять. Один из вариантов, как вы видели ранее, проговаривать ответ вслух по ходу решения. Но для большего драматизма вы можете предпочесть, как и я, удерживать ответ в памяти с помощью пальцев и произносить его целиком в самом конце. В таком случае, вы можете столкнуться с проблемой при запоминании чисел, которые больше пяти, ведь, как и большинство из нас, вы располагаете лишь пятью пальцами на каждой руке. Решением является специальная техника, в основе которой язык жестов. Я называю её «Правило большого пальца». Она наиболее эффективна для запопинания чисел, состоящих из трёх и более цифр. Эта техника полезна не только в данной Главе, но также пригодиться и в последующих, где придётся иметь дело с задачками побольше и с числами подлиннее.
Вы уже знаете, что для представления чисел от 0 до 5, всё, что вам нужно сделать, это поднять эквивалентное количество пальцев на руке. Когда ваш большой палец вовлечён в процесс, лёгким становится представление чисел от 6 до 9. Вот список правил большого пальца:
Чтобы задать 6, разместите большой палец на верхней части вашего мизинца.
Чтобы задать 7, поместите большой палец на верхней части безымянного пальца.
Чтобы задать 8, поместите большой палец на верхней части среднего пальца.
Чтобы задать 9, поместите большой палец на верхней части указательного пальца.
При работе с трёхзначным числом, задайте цифры для сотен на левой руке и цифры для десятков на правой. Когда дело дойдёт до одной цифры, вы достигните конечной точки решения (за исключением возможного остатка). Теперь произнесите число на вашей левой руке, число на вашей правой руке, последнюю цифру, которую только что посчитали, и остаток (что у вас в голове). Вуаля - вы произнесли ответ!
В целях практики попробуйте решить следующую задачку на деление четырёхзначного числа:
|
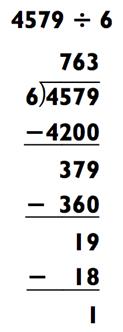
Используя правило большого пальца для запоминания ответа, вы зададите 7 на вашей левой руке, путём соединения большого пальца с безымянным, и зададите 6 на вашей правой руке с помощью соединения большого пальца с мизинцем. Как только вы вычислите последнюю цифру (которая равна 3) и остаток (который равен 1), вы
можете «зачитать» итоговый ответ с ваших рук слева направо: «семь…
шесть…три с остатком один, или одна шестая.»
Некоторые задачи на деление четырёхзначных цифр дают четырёхзначный ответ. В таком случае, раз уж у вас только две руки, вы будете вынуждены вслух произнести цифру для тысячи и использовать правило большого пальца для запоминания остального ответа. Например:
|
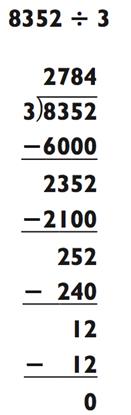
Для решения этой задачи, вы делите 8 на 3, чтобы получить цифру для тысячи в виде 2; произносите «две тысячи» вслух, затем делите 2352 на 3 привычным способом.
Деление на двузначные числа
К данному разделу мы подходим с предположением, что вы уже освоили искусство деления на одну цифру. Естественно, задачи на деление становятся сложнее с увеличением делителя. К счастью, я припас немного магии в рукаве, чтобы сделать вашу жизнь легче.
Давайте начнем с относительно легкой задачи:
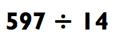
Так как 597 находится между 14 х 10 и 14 х 100, ответ (так же называемый как «частное») будет находится между 10 и 100. Чтобы определить ответ, вам в первую очередь нужно задаться вопросом:
«Сколько раз по 14 даст в сумме 590?» Потому что 14 х 40 = 560, вы будете знать, что ответ находится в районе 40>, так что вы можете произнести «сорок» вслух.
Далее, вычитаем 560 из 597, что даёт нам 37 и сводит задачу к делению 37 на 14. Так как 14 х 2 = 28, ваш ответ 42. Вычитая 28 из 37, мы получаем остаток 9. Процесс выведения решения задачи может быть показан на рисунке следующим образом:
|
|
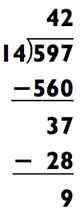
В данном примере ответ будет двузначным числом, так как 682 находится между 23 х 10 = 230 и 23 х 100 = 2300. Чтобы найти цифру для десятка двузначного числа, вам нужно спросить себя: «Сколько раз по 23 даст в сумме 680?» Если вы попробуете 30, то увидите, что это слегка перебор, так как 23 х 30 = 690. Теперь вы в курсе, что ответ находится в районе 20>, и вы можете произнести это. После вычтите 23 х 20 = 460 из 682 для получения 222. Так как 23 х 9 = 207, ответ
будет 29 с остатком 222 - 207 = 15.
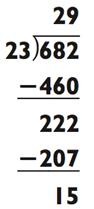
ОТВЕТ: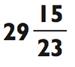 
Теперь рассмотрим:
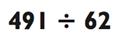
Так как 491 меньше, чем 62 х 10 = 620, ваш ответ будет просто цифрой с остатком. Вы можете попробовать угадать 8, но 62 х 8 = 496,
а это немножко больше. Так как 62 х 7 = 434, ответ будет 7 с остатком
491 - 434 = 57 или 7 и 57/62. 
ОТВЕТ: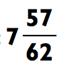 
В действительности, есть отличный трюк, который может облегчить решение таких задач. Помните, как вы сначала пытались перемножить 62 х 8, но обнаружили, что это больше, чем нужно? Ну, это было не напрасно. Помимо информации о том, что ответ будет 7, вы также можете сразу определить остаток. Так как 496 на 5 больше, чем 491, остаток будет на 5 меньше, чем 62, делитель. Раз уж 62 - 5 = 57, то ваш ответ 7 и 57/62. Причина, по которой данный трикс работает, в том, что 491 = (62 х 8) - 5 = 62 х (7 + 1) - 5 = (62 х 7 + 62) - 5 = (62 х 7) + (62 - 5) = 62 х 7 + 57.
Теперь попробуйте посчитать 380 ÷ 39, используя «срезку»,
которую только что выучили. Итак, 39 х 10 = 390, что больше на
10. Следовательно, ответ будет 9 с остатком 39 - 10 = 29.
Следующий вызов для вас - деление четырёхзначного числа на двузначное:
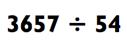
Так как 54 х 100 = 5400, вы знаете, что ваш ответ будет двузначным числом. Чтобы получить первую цифру ответа, вам необходимо выяснить, сколько раз по 54 даст в сумме 3657. Так как 54 х 70 = 3789 (это немножко больше), вы будете знать, что ответ где-то в районе 60>.
Далее, умножьте 54 х 60 = 3240 и вычтите 3657 - 3240 = 417.
Как только вы произнесёте 60, ваша задача будет упрощена до
417 ÷ 54. Раз уж 54 х 8 = 432 (что тоже слегка больше), ваша последняя цифра будет 7 с остатком 54 - 15 = 39.
|
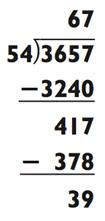
Теперь попробуйте свои силы на задачке с трёхзначным частным:
|
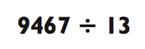
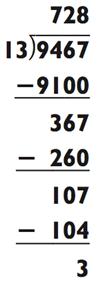
Упрощае м задачи на деление
Если к этому моменты вы страдаете мозгового перенапряжения, расслабьтесь. Как и было обещано, я хочу поделиться с вами несколькими приёмами для упрощения определённых задач на деление в уме. Эти приёмы основаны на принципе деления обоих частей задачи на общий множитель. Если оба числа в задаче чётные, вы можете вдвойне упростить проблему путём деления каждого числа на 2 перед тем как начать. Например, 858 ÷ 16 содержит два чётных числа, и деление их на 2 ведёт к значительно более простой задаче 429 ÷ 8:
|
|
|
|
Как вы сами видите, остатки 10 и 5 отличаются; но если вы запишите остаток в форме дроби, то получите 10/16, что и есть 5/8. Следовательно, используя данный метод, вы всегда должны выражать ответ в форме дроби.
Мы проделали оба типа вычислений для того, чтобы вы увидели, насколько это легче. Теперь ваша очередь практиковаться:
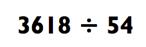
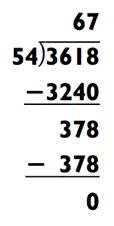РАЗДЕЛИМ НА 2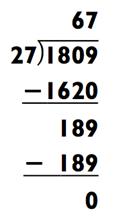 
ОТВЕТ: 67
Пример справа намного легче решить в уме. Если вы очень встревожены, то можете разделить обе части исходной задачи на 18 для получения ещё более простой задачи: 201 ÷ 3 = 67.
Выжидайте задачки, которые можно подвергнуть делению на 2
дважды, такие как:
Мне всегда кажется, что проще дважды разделить проблему на 2, чем делить каждое из чисел на 4. А теперь, когда оба числа оканчиваются на 0, вы можете разделить каждое на 10:
|
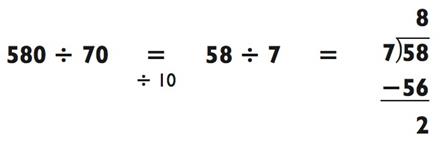
Если оба числа заканчиваются на 5, удвойте их, а затем разделите на 10 для упрощения задачи. Например:
|
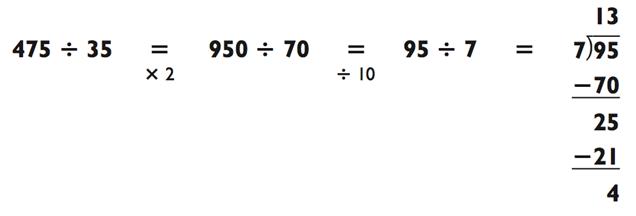
Наконец, если делитель оканчивается на 5, а делимое на 0, то умножьте оба на 2, а затем разделите на 10, прямо как мы делали выше:
|
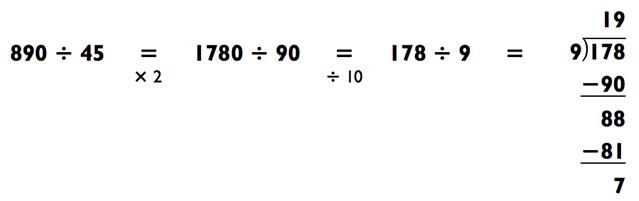
Тестирование на делимость
В последнем разделе мы увидели, как задачки на деление могут быть упрощены, если оба числа поделить на общий множитель. Мы закончим эту главу кратким обсуждением того, как определить, является ли одно число множитилем другого. Возможность определить множитель числа помогает нам упростить задачу на деление и может ускорить процесс решение многих задач на умножение. Это также будет очень полезным инструментом, когда мы доберёмся до продвинутого умножения, где вы частенько будете искать способы разложить на множители двух-, трех-, или даже пятизначный числа посреди решения задачки на умножение. Способность быстро разлагать эти числа будет весьма полезна. И кроме того, я думаю, что некоторые из правил просто сами по себе прекрасны.
Легко проверить, делится ли число на 2. Всё, что вам нужно сделать, это проверить, является ли последняя цифра чётной. Если последняя цифра 2, 4, 6, 8, или 0, то и число целиком делится на 2.
Чтобы протестировать число на способность делится на 4, проверьте, делится ли последняя цифра двузначного числа на 4. Число 57 852 кратно 4, потому что 52 = 13 х 4. Число 69 346 не кратно 4, поскольку 46 не кратно 4. Причина, по которой это работает, состоит в том, что 4 делит равномерно делит 100 и, следовательно, в любое кратное 100 число. Отсюда, так как 4 равномерно делит в 57 800, и 52
делится на 4, мы знаем, что 4 равномерно поделит их сумму, 57 852.
По такому же принципу, так как 1000 делится на 8, для теста на делимость 8, проверьте последние три цифры числа. Число 14 918 делится на 8 как 918. Но раз уж такое действие завещает нам остаток (918 ÷ 8 = 114 6/8), то это число не делится на 8. Вы также могли наблюдать это, если заметили, что 18 (последние две цифры 14 918) не
делится на 4, а так как 14 918 не делится на 4, оно не может делиться и на 8.
Когда дело доходит до делимости на 3, предлагаю вам воспользоваться классным правилом, которое легко запомнить: число делится на 3 тогда, и только тогда, когда сумма составляющих его цифр делятся на 3 (независимо от того, сколько цифр в числе). Для проверки того, делится ли 57 852 на 3, просто сложите 5 + 7 + 8 + 5 + 2
= 27. Так как 27 кратно 3, то мы теперь знаем, что 57 852 кратно 3. Такое же удивительное правило справедливо для делимости на 9. Число делится на 9 тогда, и только тогда, когда сумма составляющих его цифр кратна 9. Следовательно, 57 852 кратно 9 , тогда как число 31 416, которое в сумме даёт 15, вовсе нет. Причина, по которой это работает, основана на том, что числа 1, 10, 100, 1000, 10000, и так далее, всегда на единицу больше, чем кратное 9.
Число делится на 6 тогда, и только тогда, когда оно чётное и делится на 3. Так что легко провести тест на делимость на 6.
Установить, делится ли число на 5, ещё проще. Любое число, независимо от своей величины, кратно 5 тогда, и только тогда, когда оно оканчивается на 5 или 0.
Установление делимости на 11 почти такое же простое, как определение делимости на 3 или 9. Число делится на 11 тогда, и только тогда, когда вы придёте либо в 0, либо к кратному 11 в результате попеременного вычитания и сложения составляющих число цифр. Например, 73 958 не делится на 11 , так как 7 - 3 + 9 - 5 + 8
= 16. Однако числа 8492 и 73 194 кратны 11, так как 8 - 4 + 9 - 2 = 11 и 7
- 3 + 1 - 9 + 4 = 0. Причина, по которой это работает, основана, как и правило для 3 и 9, на том, что числа 1, 100, 10 000, 1 000 000 на
единицу больше, чем один кратное 11, в то время как числа 10, 1000, 100 000, и так далее на единицу меньше величины, кратной 11.
Тестирование делимости на 7 немного сложнее. Если вы прибавляете (вычитаете) число, которое кратно 7, к (из) числу(а), которое вы тестируете, и полученное число делится на 7, то результат теста положительный. Я всегда выбираю, чтобы прибавляемое или вычитаемое кратное 7, было таким, что в результате сумма или разность заканчивалась бы на 0. Например, для проверки числа 5292, я вычитаю 42 (кратное 7), чтобы получить 5250. Далее, я избавляюсь от 0 на конце (так как деление на десять не влияет проверку делимости на семь), получая в итоге 525. Затем я повторяю процесс, прибавляя 35 (кратное 7), что дает мне 560. Когда я удаляю 0, то остаюсь с числом 56, которое, как мне известно, кратно 7. Таким образом, исходное число 5292 является делимым на 7.
Этот метод работает не только для 7, но и для любого нечетного числа, которое не оканчивается на 5. Например, чтобы проверить, делится ли 8792 на 13, вычитаем 4 х 13 = 52 из 8792 для получения
8740. Опуская 0, имеем следствием 874. Затем прибавляем 2 х 13 = 26, чтобы получить 900. Удаление двух 0 оставляет вас с числом 9, которое, очевидно, не кратно 13. Таким образом, 8792 не кратно 13.
Обыкновенные дроби
Если вы в состоянии управиться с целыми числами, то арифмитические действия с дробями будет почти таким же лёгким. В этом разделе мы сделаем обзор основных методов сложения, вычитания, умножения, деления и упрощения обыкновенных дробей. Те, кто уже знаком с дробями, могут пропустить тот раздел без ущерба для целостности.
Деление обыкновенных дробей
Деление дробей такое же лёгкое, как и умножение. Тут только одно дополнительное действие. Сперва переверните левую дробь с ног на голову (это называется «обратная дробь»), а затем умножайте. Например, обратная дробь для 4/5 будет 5/4. Следовательно,
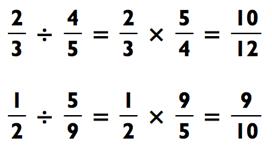
Упражнение: упрощение дроби
Можете ли вы найти равную дробь со знаменателем 12 для дробей, представленных ниже?
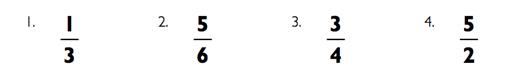
Упростите эти дроби.
Сложение дробей
Данное действие можно считать простым, когда знаменатели равны. Если это так, значит мы складываем числители и сохраняем прежний знаменатель.
Например,
Иногда мы можем упростить наш ответ. Например,
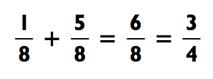
Вычитание дробей
Вычитание дробей довольно-таки похоже на их сложение. Мы проиллюстрировали это примерами и обеспечили вас тренировочными упражнениями.
Колонки чисел
Сложение длинных колонок чисел - как раз та самая задача, с которой вы можете столкнуться по работе или во время разбора личных финансов. Сложите числа из следующего столбика привычным способом и затем проверьте то, как я это сделал.
Когда у меня в распоряжении имеется ручка с бумагой, я складываю числа сверху вниз и справа налево - прямо как нас учили в школе. С практикой, вы сможете решать эти задачи в уме также быстро (или быстрее), как и на калькуляторе. Когда я суммирую цифры, единственный числа, которые я «слышу»,
- это частичные суммы. Это когда я сперва суммирую первую колонку (крайнюю справа) 8 + 4 + 0 + 7 + 7 + 5, я слышу 8…12 . . . 19 . . . 26 . . . 31. Затем я записываю 1, держу в уме 3 и вывожу результат. Следующая колонка бы звучала как 3 . . . 5 . . . 13 . . . 15 . . . 22 . . . 23 . . . 25. Как только я получаю итоговый ответ, я записываю его, затем проверяю свои вычисления путём сложения чисел снизу вверх и, я надеюсь, получаю такой же ответ.
Например, итоги первой колонки будут подведены снизу вверх в виде 5 + 7 + 7 + 0 + 4 + 8 (что у меня в голове звучит как 5 . . . 12 . . . 19 .
. . 23 . . . 31). Затем я мысленно переношу цифру 3 и складываю 3 + 2 + 1 + 7 + 2 + 8 + 2, и так далее. Через сложение чисел в другом порядке вы снижаете вероятность совершить одинаковую ошибку дважды. Конечно, если ответ отличается, тогда хотя бы одно из вычислений дожно быть неправильным.
Модульные суммы
Если я не уверен на счёт своего ответа, то иногда проверяю решение, используя метод, который я называю модульные суммы (потому что он основан на элегантной математике из раздела модульной арифметики). Этот метод также известен под именами
«цифровые корни» и «метод сравнений по модулю 9». Я признаю, что он не такой уж практичный, но зато лёгок в использовании.
С методом модульных сумм вы складываете цифры каждого из чисел до тох пор, пока не останетесь с одной единственной цифрой. Например, чтобы вычислить модульную сумму 4328, сложите 4 + 3 + 2 +
8 = 17. Затем сложите цифры числа 17, чтобы получить 1 + 7 = 8. Следовательно, модульная сумма 4328 будет 8. Для предыдущей задачки модульная сумма каждого из чисел вычисляется следующим образом:
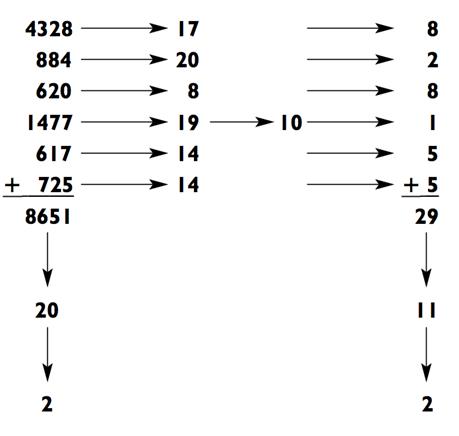
Как проиллюстрировано выше, следующий шаг - сложение всех модульных сумм вместе (8 + 2 + 8 + 1 + 5 + 5). Это даёт 29, что в сумме 11, что в свою очередь в сумме 2. Обратите внимание, что модульная сумма 8651, ваш набор цифр исходного числа, тоже равняется 2. Это не совпадение! Если вы посчитали ответ и модульную сумму правильно, то ваша итоговая модульная сумма должна быть такой же. Если они различаются, то вы определённо допустили где-то ошибку: существует шанс (около 1 к 9), совпадение модульных сумм будет случайным. Если существует ошибка, тогда этот метод позволит обнаружить её 8 раз из 9.
Метод модульных сумм в большинстве случаев известен математикам и бухгалтерам больше как «метод сравнений по модулю 9», потому что модульная сумма числа обыкновенно равняется остатку, полученному в результате деления на 9. В случае, когда ответ выше (8651), модульная сумма была 2. Если вы разделите 8651 на 9, ответ будет 961 с остатком 2. Другими словами, если вы будете отбрасывать
9 из 8651 в общей сумме 961 раз, то будете иметь остаток 2. Существует одно маленькое исключение. Напомним, что сумма цифр любого кратного 9 также является кратной 9. Отсюда, если число является кратным 9, оно будет иметь модульную сумму 9, даже если остаток равен 0.
Вычитание на бумаге
Вы, конечно, не можете вычитать колонки чисел таким же способом, как вы складываете их. Предпочтительнее вычитать их число за числом, что означает: все задачи на вычитание включают лишь два числа. Ещё раз: с карандашом и бумагой в нашем распоряжении легче вычитать справа налево. Чтобы проверить своий
ответ, просто прибавьте его ко второму числу. Если всё правильно, тогда вы должны получить верхнее число.
Если хотите, то также можете использовать модульные суммы для проверки вашего ответа. Ключ в том, чтобы вычитать полученные модульные суммы и затем сравнивать полученное число с модульной суммой вашего ответа:
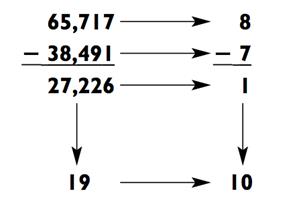
Существует ещё одно ухищрение. Если разница модульных сумм будет отрицательной или равна 0, прибавьте к ней 9. Например:
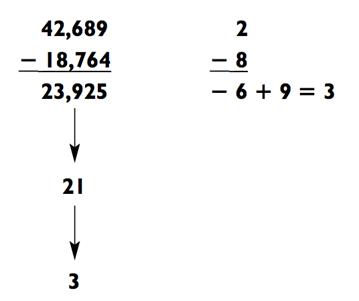
Квадратные корни на бумаге
С появлением карманных калькуляторов, метод ручки с бумагой для расчёта квадратного корня практически превратился в потерянное искусство. Вы уже видели как устно прикидывать квадратные корни.
Сейчас я покажу вам как это делать точно с использованием ручки и бумаги.
Помните, как при приближённой оценке квадратных корней вы рассчитывали квадратный корень девятнадцати? Давайте взглянем на проблему ещё раз, на этот раз используя метод, который даст вам точный квадратный корень.
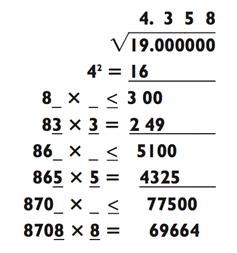
Я опишу его в общем случае, который годится для любой ситуации, и проиллюстрирую примером выше.
Шаг 1. Если количество цифр после запятой равно одному, трём, пяти, семи или любому другому нечётному числу, то первая цифра ответа (или частного) будет наибольшим числом, чей квадрат меньше половины первой цифры исходного числа. Если количество цифр после запятой равно двум, четырём, шести или любому другому чётному числу, то первая цифра частного будет наибольшим числом, чей квадрат меньше первых двух цифр делимого. В данном случае, 19 является двузначным числом, так что первая цифра частного будет наибольшим числом, чей корень квадратный меньше 19.
Шаг 2. Вычтите квадрат числа с Шага 1, затем снесите ещё две цифры. Так как 42 = 16, мы отнимаем 19 - 16 = 3. Мы переносим два 0, оставляя 300 в качестве текущего остатка.
Шаг 3. Удвойте существующее частное (игнорируя знаки после запятой) и оставьте пустое место после него. Здесь 4 х 2 = 8. Запишите 8_ х _ слева от текущего остатка (300 в данном случае).
Шаг 4. Следующая цифра частного будет наибольшим числом, которое может заполнить пропуски, so that the resulting multiplication problem is less than or equal to the current remainder. В данном случае, этим числом будет 3, потому что 83 х 3 = 249, тогда как 84 х 4 = 336, что слишком много. Запишите это число над второй цифрой следующих двух чисел; в данной ситуации цифра 3 будет находится над вторым 0. Теперь мы имеем частное в размере 4,3.
Шаг 5. Если вы хотите больше цифр, вычтите произведение из остатка (например, 300 - 249 = 51) и снесите следующие две цифры; в данном случае 51 превратиться в 5100, что станет текущим остатком. Теперь повторите шаги 3 и 4.
Для получения третьей цифры квадратного корня, удвойте частное, снова игнорируя всё после запятой (например, 43 х 2 = 86). Поместите 86_ х _ слева от 5100. Цифра 5 даст нам 865 х 5 = 4325, наибольшее произведение, которое меньше 5100. Пятёрка будет сверху над следующими двумя числами, в данном случае, двумя 0. Теперь мы имеем частное в размере 4,35. Для ещё большего количества цифр после запятой, повторите процедуру, как мы и сделали в примере.
Вот пример нечётного количества цифр поред запятой:
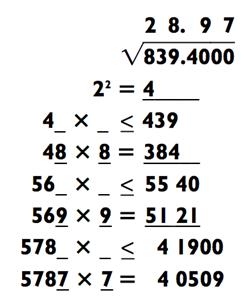
Далее мы вычислим квадратный корень четырёхзначного числа. В данном случае (как и с двузначными числами) мы учитываем первые две цифры примера для определения первой цифры квадратного корня:
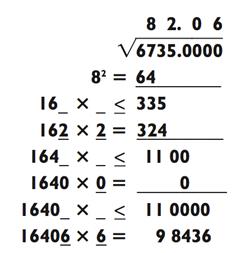
Наконец, если число, для которого вы рассчитывает квадратный корень, имеет правильный (полный) квадрат, вы узнаете об этом сразу же, как получите в итоге нулевой остаток и когда ничего не придётся сносить. Например:
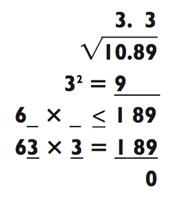
Умножение на бумаге
Для умножения с ручкой и бумагой я использую метод «крест- накрест», который позволяет мне записать весь ответ целиком в одну строчку, нигде не записывая промежуточные результаты! Это одна из самых впечатляющих демонстраций матемагии, когда в вашем распоряжении есть ручка с бумагой. Многие молниеносные вычислители из прошлого заработали себе репутацию этим методом. Они получали два громадных числа и записывали ответ почти мгновенно. Методу «крест-накрест» лучше всего обучаться на примере.
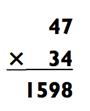
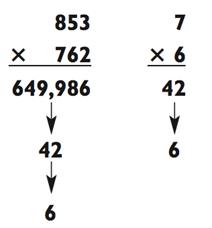
Шаг 1. Сначала умножьте 4 х 7 для получения 28, запишите 8 и мысленно перенесите 2 на следующее вычисление ниже.
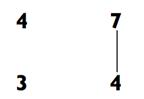
Шаг 2. Следуя схеме, сложите 2 + (4 х 4) + (3 х 7) = 39, запишите
9 и мысленное перенесите 3 на итоговую калькуляцию ниже.
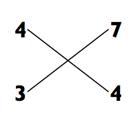
Шаг 3. Закончите сложением 3 + (3 х 4) = 15 и запишите 15 для получения итогового ответа.
Вы только что записали ответ: 1598.
Давайте решим другую задачу «2-на-2», используя метод «крест-
накрест»:
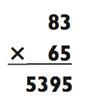
Список шагов и схемы выглядят следующим образом:
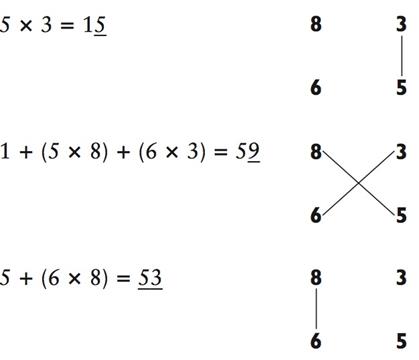
Ответ: 5395
|
ниже:
Мы поступили так, как предложено в нашей собственной модели
Ответ: 649 986
Обратите внимание, что количество умножений на каждой стадии составляет 1, 2, 3, 2 и 1 соответственно. Математика, лежащая в основе метода «крест-накрест», не более чем распределительный закон. Например, 853 х 762 = (800 + 50 + 3) х (700 + 60 + 2) = (3 х 2) + [(5
х 2) + (3 х 6)] х 10 + [(8 х 2) + (5 х 6) + (3 х 7)] х 100 + [(8 х 6) + (5 х 7)] х
1000 + (8 х 7) х 10 000, что в точности является вычислением по методу
«крест-накрест».
|
Если модульные суммы не совпадают, то вы допустили ошибку.
Данный метод распознаёт ошибку, в среднем, 8 раз из 9.
В случае с примером «3-на-2», процедура такая же, за исключением того, что вы рассматриваете цифры-сотни второго числа как нули:
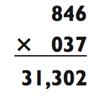
Ответ: 31 302
Конечно на практике, вы, как правило, просто проигнорируете умножение на нуль. Вы можете использовать метод «крест-накрест» для решения задачек любого размера. Для получения ответа на задачу
|
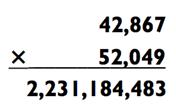
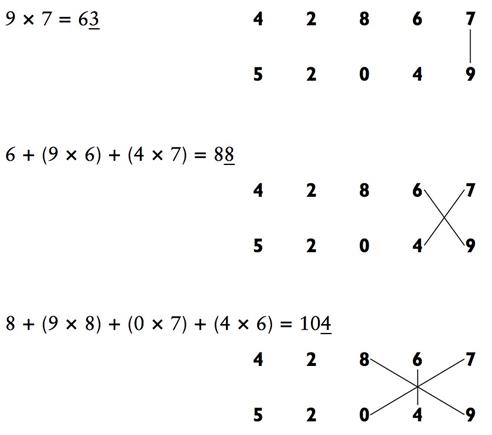
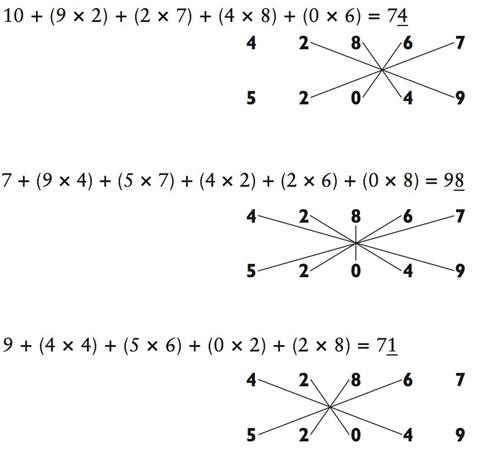
Ответ: 2 231 184 483
Вы можете проверить себя, используя метод модульных сумм.
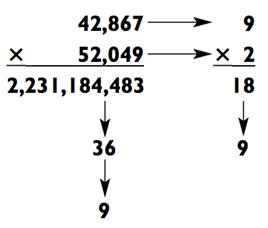
Умно ж ение «3- на -2»
Мы уже видели во время решение задачек типа «2-на-2», что существует несколько разных путей решения одного и того же примера. Многообразие методов увеличивается, когда вы увеличиваете количество цифр в задаче. При умножения «3-на-2» я нахожу выгодным «предварительный осмотр» примера для определения метода расчёта, который подвергнет мозг наименьшей нагрузке.
Факторинговый метод
Самые лёгкие задачи «3-на-2» это те, в которых двузначные числа можно разложить.
Например:
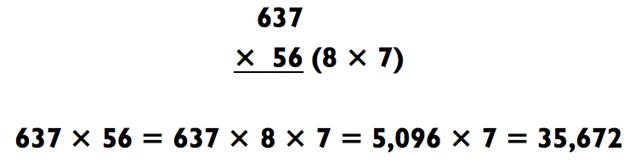
Они потрясные, потому что вам не нужно ничего прибавлять. Вы просто раскладываете 56 как 8 х 7, затем решаете пример «3-
на-1» (637 х 8 = 5096) и, наконец, пример «4-на-1» (5096 х 7 = 35 672).
Больше нет никаких дополнительных действий, и отсутствует нужда в запоминании промежуточных результатов.
Больше половины всех двузначных чисел можно разложить на числа типа 11 и ниже, так что вы будете в состоянии использовать данный метод для многих задач. Вот пример:
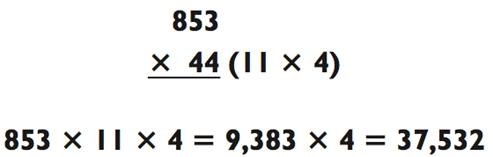
Чтобы умножить 853 х 11, представьте 853 в виде 850 + 3 и продолжайте в следующем ключе:
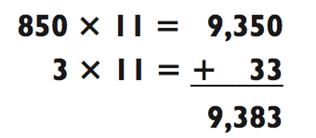
Теперь умножьте 9383 х 4, представив 9383 как 9300 + 83
следующим образом:
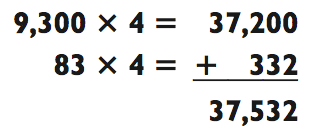
Если двузначное число не раскладывается на меньшие числа, изучите трёхзначное на предмет такой возможности:
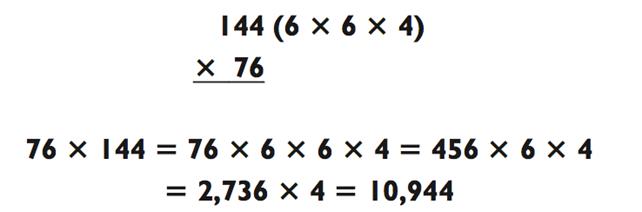
Обратите внимание на то, что последовательность умножения выстроилась из задач «2-на-1», «3-на-1» и, наконец, «4-на-1». Раз уж это все те задачи, которые сейчас уже можете решать значительной легкостью, такой тип задач «3-на-2» в принципе не должен стать проблемой для вас.
Вот ещё один пример, где двузначное число не подвергается факторизации, но зато трёхзначное число - да:
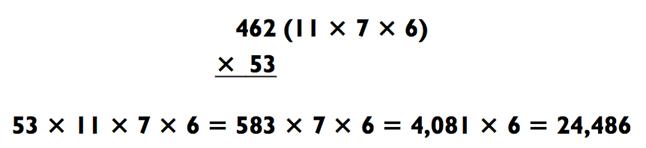
Здесь последовательность «2-на-2», «3-на-1» и «4-на-1», хотя, когда трёхзначное число разлагается на 11, вы можете использовать метод умножения на 11 и получить легкий пример «2-на-2» (53 х 11 = 583). В данном случае, признание возможности разделить число на 11 оправдывает себя (как было описано в Главе 4).
Если двузначное число не раскладывается, а трёхзначное раскладывается только в виде «2-на-1», с задачей всё ещё можно легко найти общий язык путём умножения «2-на-2», а затем «4-на-1»:
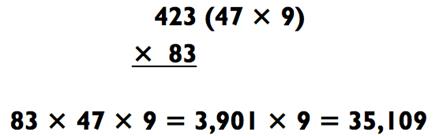
Здесь вам необходимо будет увидеть то, что 423 делится на 9, ставя перед нами задачу 83 х 47 х 9. Такая задача «2-на-2» не такая уж и простая, но если представить 83 как 80 +3, то вы получите:
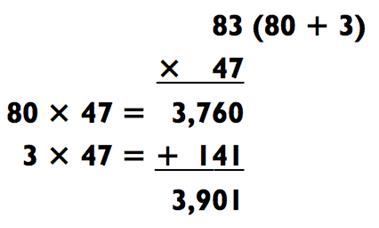
Затем решите задачу «4-на-1» в виде 3901 х 9 для получения итогового ответа в размере 35 109.
Метод сложения
Если двух и трёхзначное числа в задаче «3-на-2» не поддаются простому разложению, вы всегда можете прибегнуть к методу сложения:
Данный метод требует от вас сложения результатов задачи «2- на-2» и «2-на-1». Такого рода задачи имеют в себе более сожные элементы (нежели те, которые могут быть факторизованы) так как вы вынуждены решить пример «2-на-1», держа в уме пятизначное число, а затем сложить результаты вместе. В действительности, возможно даже будет проще решить эту задачу путём разложения 721 как 103 х 7 и последующего вычисления 37 х 103 х 7 = 3811 х 7 = 26 677.
Вот другой пример:
Хотя вы обычно будете разбивать трёхзначное число во время использования метода сложения, порой разбитие двузначного числа вместо этого бывает более выгодным, в особенности когда последние цифры двузначного числа это 1 или 2, как в следующем примере:
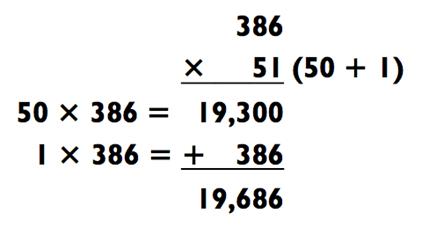
Это сокращает «3-на-2» до «3-на-1», делая нашу задачу особенно лёгкой, так как второе действие на умножение включает 1. Заметьте также, что нам была оказана помощь в виде умножения 5 на чётное число, что принесло дополнительный 0 в ответ, так что только одна цифра перекрывается в задаче на сложение.
Другой пример умножения 5 на чётное число проиллюстрирован на следующей задаче:
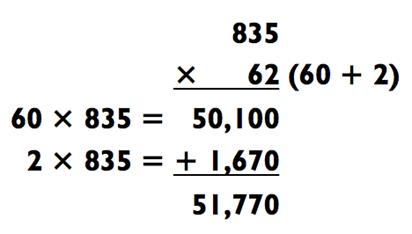
Когда вы умножаете 6 (из 60) на 5 и получаете 835, это порождает появление дополнительного 0 в ответе, делая задачу на сложение в особенности лёгкой.
Метод вычитания
Как и с примерами «2-на-2», бывает иногда проще решить задачу
«3-на-2» путём вычитания вместо сложения, как в следующих задачках:
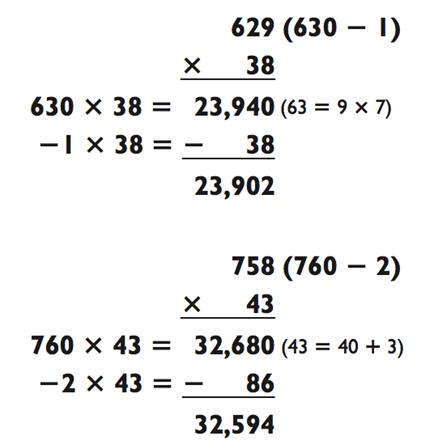
В отличии от этого, вы можете сравнить методы вычитания и сложения ниже, применив их к одной и той же задаче:
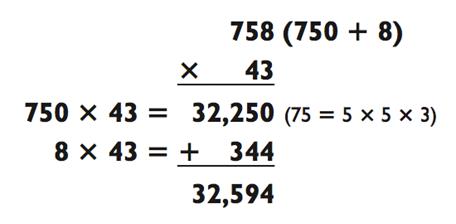
Мое предпочтение при решении данной задачи - использование метода вычитания, потому что я всегда стараюсь оставить себе максимально лёгкую задачу на сложение или вычитание на самый конец. В данном случае, я бы лучше вычел 86, чем прибавил 344, даже при том, что решение задачи типа «2-на-2» (см. выше) методом вычитания слегка тяжелее, чем методом сложения.
Метод вычитания также может быть использован с трёхзначными числами, которые меньше кратного 100 или близки к кратному 1000, как в следующих двух примерах:
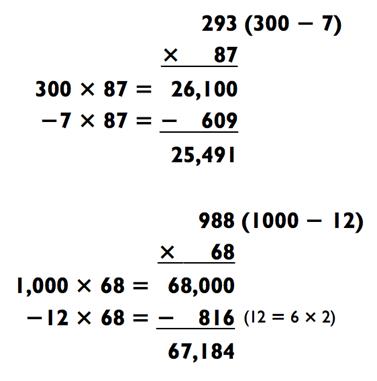
Последние три цифры ответа были получены путём использования дополнений 609 - 100 = 509 и 816, соответственно.
Наконец, на следующей иллюстрации мы поделили двузначное число с помощью метода вычитания. Обратите внимание, как мы отняли 736 путём вычитания 1000 и обратного прибавления дополнения:
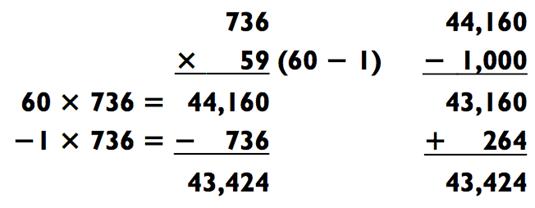
Умно ж ение «3- на -3»
На пути к продвижению к нашему грандиозному финалу в виде умножения «5-на-5», задачки типа «3-на-3» наше последний барьер. Как и в случае с «3-на-2», существует многообразие методов, которые могут быть использованы для упрощения процесса в целом.
Метод факторинга
Мы начнём с метода факторинга. К несчастью, большинство трёхзначных чисел не раскладываются на единичные цифры, но если всё-таки раскладываются, процесс вычисления будет не таким уж и плохим.
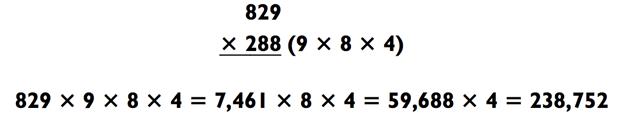
Обратите внимание на последовательность действий. Вы упрощаете задачу «3-на-3» (829 х 288) до «3-на-1-на-1-на-1». путём разложения 288 на 9 х 8 х 4. Далее это превращается в «4-на-1- на-1» (7461 х 8 х 4) и, наконец, в «5-на-1» для получения итогового ответа 238 752. Прелесть данного процесса заключается в отсутствии каких-либо действий на сложение и в том, что ничего не нужно хранить в памяти. Когда вы получили пример «5-на-1», то встали в одном шаге от выполнения задания.
Задача типа «5-на-1» может быть решена в два действия, если принять 59 688 как 59 000 + 688, а затем сложить результаты задач «2-
на-1» (59 000 х 4) и «3-на-1» (688 х 4), как показано ниже:
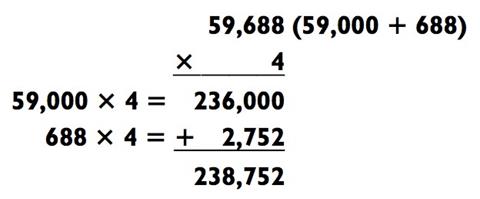
Если оба трёхзначных числа могут быть разложены как «2-на-1», тогда задача «3-на-3» может быть упрощена до «2-на-2-на-1-на-1», как в следующей задаче:
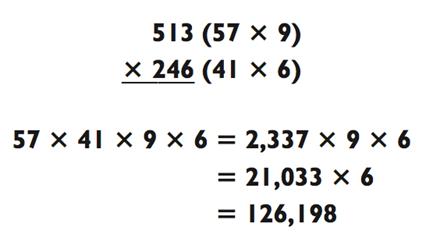
Как обычно, лучше всего сразу избавиться от тяжёлого элемента задачи (2-на-2). Как только вы сделали это, она будет сведена к «4- на-1», а затем к «5-на-1».
Почти всегда, только одно из чисел будет раскладываться. В таком случае, можно будет свести задачу к «3-на-2-на-1», как в следующем примере:
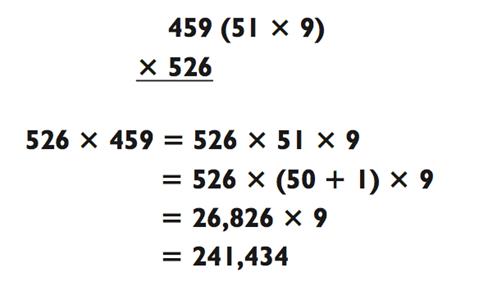
Следующая задача «3-на-3», в действительности, просто замаскированная «3-на-2»:
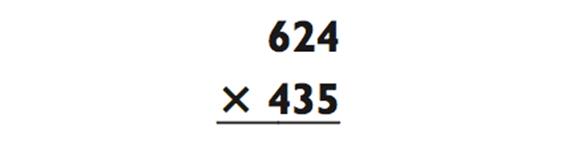
Путём удвоения 435 и сокращения 624 на половину, мы получаем эквивалентную задачу:
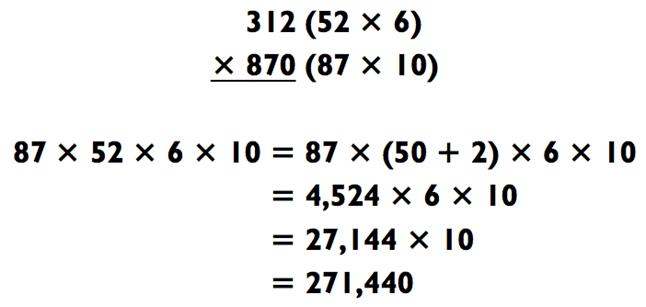
Метод совместной близости
Вы готовы к кое-чему полегче? Следующая «срезка», которую мы представили в Главе 0, основана на следующей алгебраической формуле:
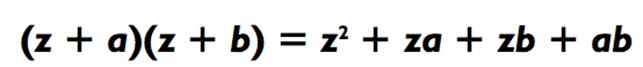
Что мы переписываем как:
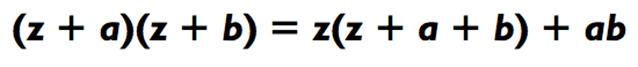
Эта формула правомерна для любых значений z, a и b. Мы будем пользоваться этим всякий раз, когда трёхзначные числа, которые нужно перемножить (z х a и z х b), находятся близко к лёгкому числу z (типичный случай - число с кучей нулей). Например, умножим:
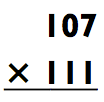
Мы будем рассматривать эту задачу как (100 х 7)(100 х 11).
Благодаря использованию z х 100, a х 7, b x 11 наша формула даёт нам:
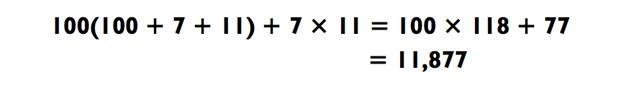
Я схематически изобразил задачу вот так:
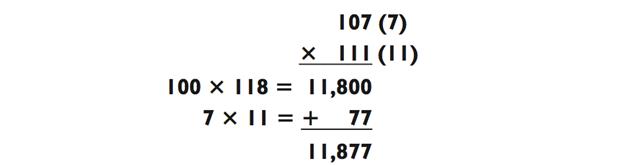
Цифры в скобках обозначают разницу между числом и нашим удобным «базовым числом» (здесь, z = 100). Число 118 может быть получено либо через сложение 107 + 11, либо через 111 + 7. По законам алгебры, обе эти суммы эквивалентны, так как (z x a) b (z x b) a.
В этот раз без лишней болтовни, вот вам ещё одна «ускорялка»:
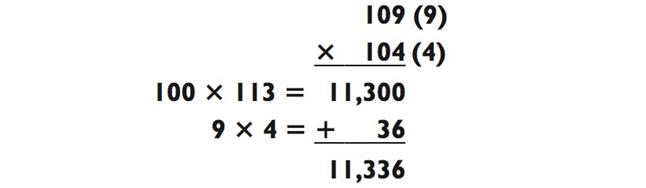
Всё чётко!
Давайте слегка поднимем ставке и возьмём базовое число побольше.
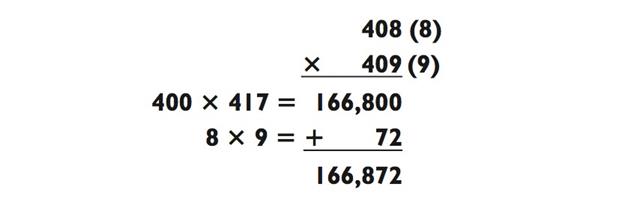
Хотя данный метод обычно и используется для умножения трёхзначных чисел, мы также можем применить его для задачи «2- на-2»:
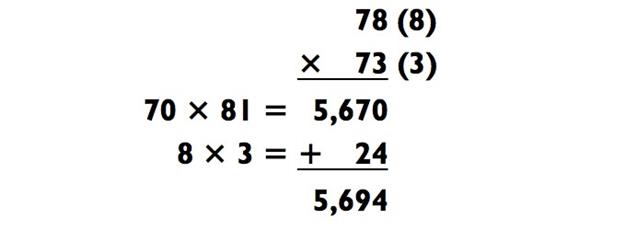
Здесь базовое число 70, его мы умножаем на 81 (78 + 3). Даже действие на сложение обычно очень простое.
Мы также можем применить данный метод, когда два числа оба меньше, чем базовое. Как, например, в следующей задачке, где оба числа меньше 400:
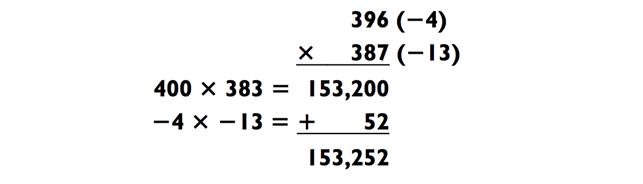
Число 383 может быть получено действием 396 - 13, или 387 - 4. Я буду использовать данный метод для задач типа «2-на-2», таких как эти:
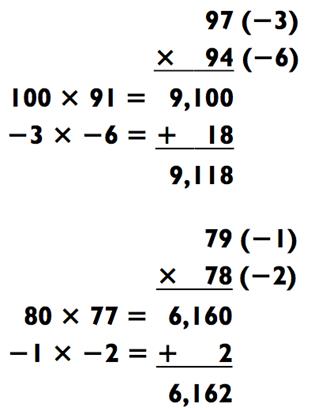
В нашем следующем примере базовое число находится между перемножаемыми числами:
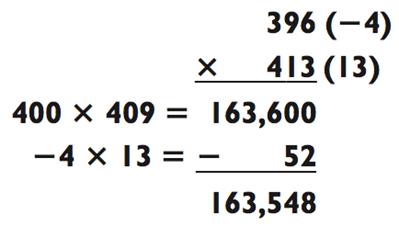
Число 409 получено по результатам 396 + 13, или 413 - 4. Обратите внимание, что с тех пор, как -4 и 13 имеют противоположные знаки, мы должны вычесть 52.
Давайте поднимем ставки ещё выше, до уровня, где второе действие требует умножения «2-на-2»:
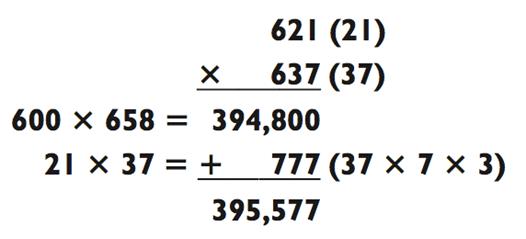
Здесь мы обращаем внимание на то, что первое действие в задачке (600 х 658) уже само по себе является разумной оценкой. Наш метод позволяет вам перейти от оценки к точному ответу.
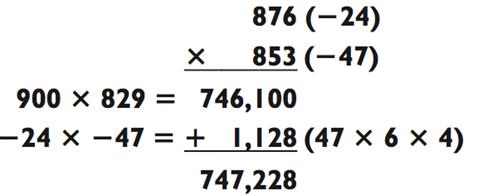
Также обратите внимание, что во всех этих примерах числа, которые мы перемножаем в первом действии, обладают такой же суммой, как и исходные числа. Например, в задачке выше, 900 + 829 = 1729, как и 876 + 853 = 1729. Это потому, что:
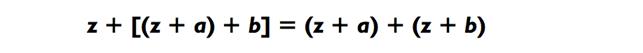
Следовательно, чтобы получить число, которое будет умножено на 900 (которое, как вы знаете, будет в районе 800>), вам всего лишь нужно взглянуть на последние две цифры 76 х 53 = 129, чтобы определить 829.
В следующем примере, сложение 827 + 761 = 1588 подсказывает нам, что следует просто умножить 800 х 788, а затем вычесть 27 х 39 следующим образом:
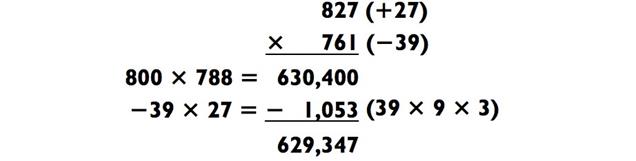
Этот метод настолько эффективен, что если задача «3-на-3», над которой вы сидите в настоящий момент, состоит из чисел далёких друг от друга, то вы можете иногда видоизменить проблему путём деления одного и умножения другого чисел на одинаковую величину (тем самым приблизив их друг к другу). Например, задача 672 х 157 может быть решена так:
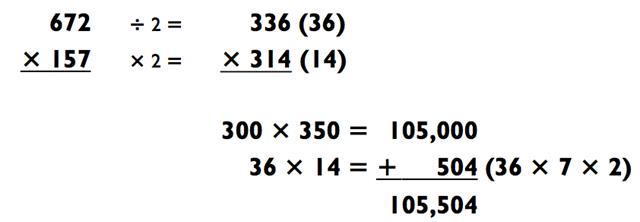
Когда умножаемые числа одинаковые (ближе друг к другу уже некуда!), обратите внимание, что вычисления методом «close-together» генерируют в точности такие же вычисления, какие вы выполняете во время традиционной процедуры возведения в квадрат:
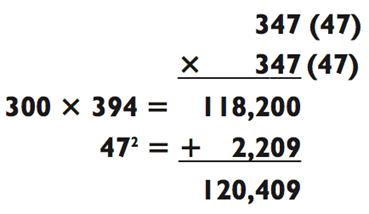
Метод сложения
Когда ни один из предыдущих методов не работает, я ищу возможность использовать метод сложения, в особенности, когда первые две цифры одного из трёхзначных чисел легки в обращении. Например, в задаче ниже, «64» из 641 раскладывается на 8 х 8, так что я бы решил её следующим образом:
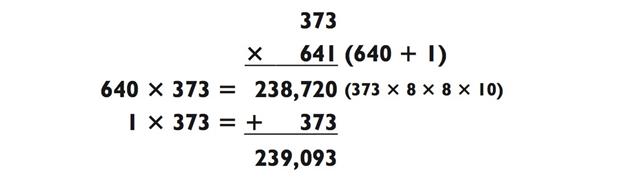
Схожим образом, в следующем примере «42» из 427 раскладывается как 8 х 8, так что вы можете использовать метод сложения и представить 427 в виде 420 + 7:
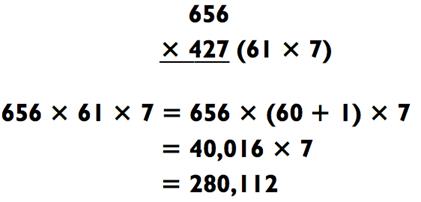
Часто я разбиваю последнюю задачку на сложение на два этапа, как здесь:
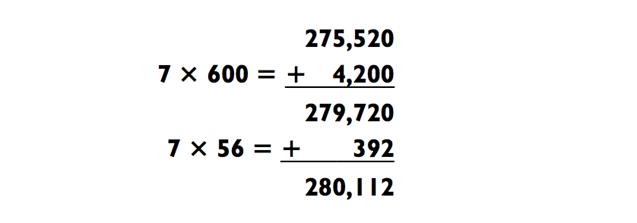
Так как задачки, которые могут быть решены методом сложения, требуют определённых усилий, я обычно сворачиваю с данной дорожки с целью найти способ, который в результате приведёт к простым вычисления в концовке. Например, задача выше могла быть решена с использованием факторинга. По сути, вот какое бы я выбрал решение:
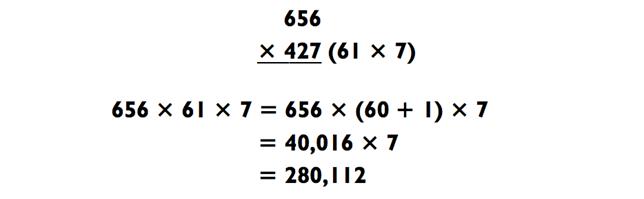
Самые простые задачи, которые могут быть решены методом сложения, содержат одно число с 0 в середине, как показано ниже:
Такие задачи, как правило, намного проще, чем другие, которые тоже можно решить таким способом. Так что стоит вглядываться в пример «3-на-3» на предмет его конвертации в такую задачу. Это окупается. Например, 732 х 308 можно было бы получить с помощью любого из «безнулевых» примеров ниже:
Мы упоминали, что другой способ решения данной задачи состоит в действии 308 х 366 х 2, и использовании преимущества близости нахождения 308 и 366. Давайте прорешаем ещё «крепкий орешек»:
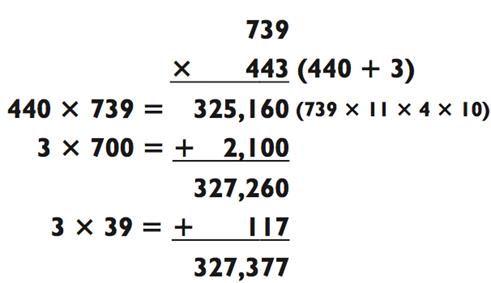
Метод вычитания
Метод вычитания - то самое орудие, которое я время от времени использую, когда одно из трёхзначных чисел может быть округлено до простого двузначного число с 0 на конце, как в следующем примере:
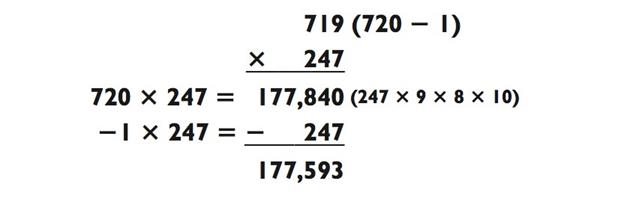
Аналогично в следующей задачке:
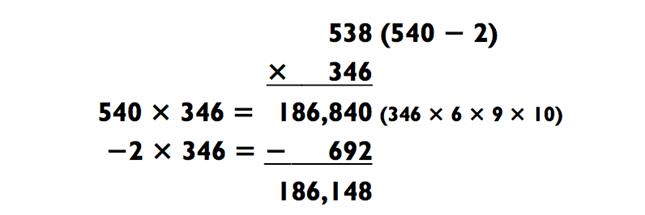
Умножение «5-на-5»
Самая огромная задача, которую мы попытаемся решить в уме, состоит из двух пятизначных чисел. Для выполнения «5-на-5» вам необходимо в совершенстве овладеть умением решать «2-на-2», «2- на-3» и «3-на-3» (а также уметь применять фонетический код). Теперь это просто вопрос соединения всего воедино. Как и при возведении в к в а д р а т п я т и з н а ч н ы х ч и с е л , в ы б у д е т е и с п о л ь з о в а т ь распределительный закон для разбития чисел на составные части. Например:
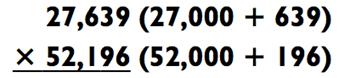
Основываясь на этом, вы можете разбить задачу на четыре более лёгких примера на умножение (что я и проиллюстрировал ниже, в стиле «крест-накрест», как «2-на-2», два «3-на-2» и, наконец, «3- на-3», просуммировав общий итог). То есть,
Как и при возведении пятизначных чисел в квадрат, я начинаю с середины, берясь за «3-на-2» (с тяжелейшего из них):
Вверив 33 228 нашей памяти с помощью кода, вы далее переключаетесь на вторую задачу «3-на-2»:
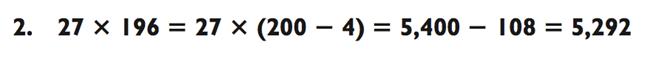
и прибавляете к числу, которое уже храните в памяти:
для получения новой суммы, которую мы храним как:
Удерживая данный код, решаем задучу «2-на-2»:
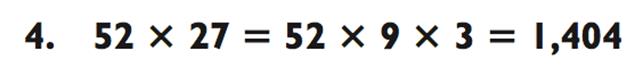
На данной стадии вы уже можете дать частичный ответ. Так как наша задача «2-на-2» представляет собой 52 х 27 миллионов, то 1404 представляет собой 1 миллиард 404 миллиона. Раз уж 404 миллиона не подразумевают переноса чисел, вы можете спокойно произнести
«Один миллиард…»
На данном этапе вы прибавляете 404 к первой половине кода (38), дабы получить 442. В этот момент вы можете сказать «…442 миллиона…» Вы можете так сделать потому, что вы знаете: на 442 не будет переноса чисел. Вы посмотрели вперёд на задачу «3-на-3», чтобы увидеть, будет ли причина для, которая к этому приведёт. Если да, то вы бы сказали «443 миллиона». Но так как предыдущий код - это 520 000, и результаты задачи «3-на-3» (639 х 196) не перевалили за 500 000 (грубая оценка 600 х 200 демонстрирует это), вы в безопасности.
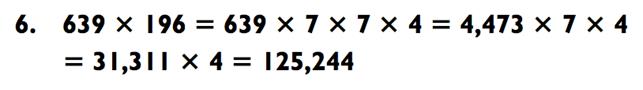
Всё ещё удерживая 520 000 (и код) в голове, вы теперь решаете
«3-на-3», используя метод факторинга, чтобы получить 125 244. Вы также могли бы перевести 244 в какой-либо код. Итоговое действие представляет собой простое сложение:
Это позволяет вам произнести оставшуюся часть ответа: «… 645 244» Так как одна картинка стоит тысячи калькуляций, вот наше изображение того, как это должно выглядеть:
Мне следует сделать здесь вставленную мимоходом заметку касательно моего предположения о том, при решении задачи типа «5- на-5» у вас есть возможность записать условия на доске или бумаге. Если нет, то вам придётся задавать мнемонический код для каждых четырёх чисел. Например, в прошлой задаче, вы могли хранить условия в виде:
Потом вы бы умножили (в соответствии с заданным кодом) 52 х 639, 196 х 27, 52 х 27 и, наконец, 196 х 639. Очевидно, это бы слегка замедлило вас, но если вас привлекают дополнительные трудности в виде отсутствия текста с числами, вы всё ещё будете в состоянии решить задачу.
Закончим главу ещё одним примером «5-на-5»:
Шаги такие же, как при решении прошлой задачи. Вы начинаете с самого сложного примера «3-на-2» и сохраняете ответ в виде кода:
Затем проводите расчёты для другого «3-на-2».
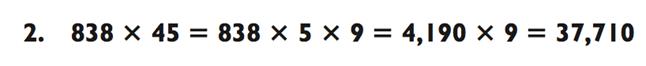
Суммируете полученное, и вверяете итог своей памяти.
Результат задачи « 2 - на- 2 » даёт вам первую цифру окончательного ответа, которую вы с уверенностью можете произнести вслух: «Три миллиарда…»
Миллионы в ответе содержат перенос цифр с 635 до 636, потому что ко второй части кода (923) достаточно лишь прибавить 77 000, чтобы бы вызвать перенос чисел. А задача «3-на-3» (838 х 547) с лёгкостью перевалит за это значение. Так что проговорите: «…636 миллионов…»
Задача «3-на-3» была посчитана с использованием метода сложения:
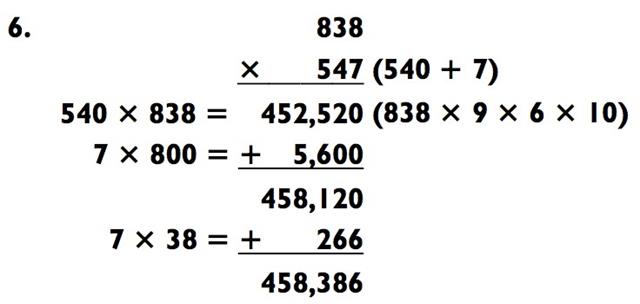
На следующем этапе вы прибавляете общую сумму ко второй части кода (923,000):
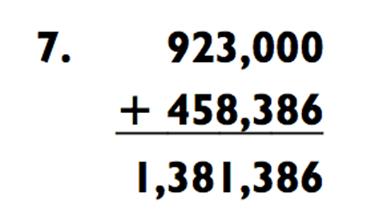
Так как вы уже использовали 1 для переноса и получения 636 миллионов, вам лишь осталось проговорить тысячи: «…381 тысяча… 386» и насладиться аплодисментами!
Данная задача может быть проиллюстрирована следующим образом:
Экстрасенсорная математика
Скажите добровольцу в аудитории: «Загадайте число, любое число». Вам также следует произнести: «Но чтобы не утруждать себя, придумайте число из одной-двух цифр». После того, как вы напомнили добровольцу, что вы никоим образом не можете знать число у него в голове, попросите следующее:
➡ Удвойте число
➡ Прибавьте 12
➡ Разделите сумму на 2
➡ Вычтите из неё исходное число
Затем скажите: «Думаете ли вы сейчас о цифре 6?» Опробуйте это сначала на себе и вы увидите, что данная последовательность всегда в итоге приводит к цифре 6, несмотря на то, какое число было изначально выбрано.
Почему это работает
Данный трюк целиком основан на простой алгебре. В действительности, я иногда использую его как способ представить алгебру студентам. Секретное число, которое выбирает ваш волонтёр,
|
(в том порядке, в котором вы их совершали):
✓ 2Х (удвоить число)
✓ 2Х + 12 (прибавить 12)
✓ (2Х + 12)/2 = Х + 6 (разделите на 2)
✓ Х + 6 - Х (вычтите исходное число)
Так что неважно, какое число выберет доброволец: итоговый ответ всегда будет 6. Если вы будете повторять данный приём, попросите добровольца прибавить другое число на втором шаге (скажем, 18). Итоговый ответ будет половиной этого числа (а именно 9).
Магическое 1089!
А вот трикс, существующий уже который век. Сделайте так, чтобы человек из аудитории достал ручку с бумагой и:
Тайно записал трёхзначное число, цифры которого идут в порядке уменьшения (как 851 или 973).
Перевернул число задом наперёд и отнял это значение из исходного числа
Полученный ответ прибавил к исходному числу, записанному задом наперёд
В конце последовательности, магическим образом появится ответ 1089, несмотря на то, какое число выбрал ваш доброволец. Например:
Почему это работает
Неважно, какое трёхзначное число вы или кто-либо другой выберете в этой игре, окончательный ответ всегда будет 1089. Почему? Обозначим АВС как неизвестное трёхзначное число. Алгебраически, это равняется:
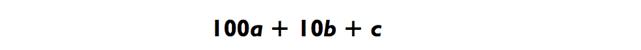
Когда вы переворачивает число и вычитаете его из исходника, то получаете число СВА, которое алгебраически равно:
После вычитания СВА из АВС, вы получаете:
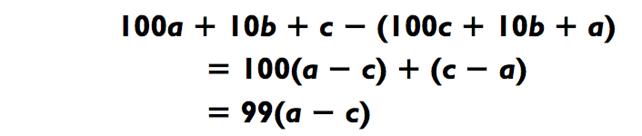
Следовательно, после вычитания на шаге 2, мы должны получить одно из следующих кратных 99: 297, 396, 495, 594, 693, 792 или 891, каждое из которых в итоге даст 1089 после прибавления к нему своей перевёрнутой версии, как мы и поступаем на шаге 3.
Трюк с пропущенной цифрой
Используя 1089 из прошлого действия, вручите добровольцу калькулятор и попросите его умножить 1089 на трёхзначное число (на
его вкус), но не говорить вам, что это за число. (скажем, он тайно умножит 1089 х 256 = 278 784) Теперь спросите, сколько цифр в полученном ответе. Ответ будет: «Шесть».
Дальше вы говорите: «Громко назовите пять из этих шести цифр в любом порядке. Я попытаюсь определить недостающую». Предположим, волонтёр выкрикивает: «Два…четыре…семь…восемь… восемь». Вы вежливо говорите ему, что он пропустил цифру 7. Секрет основан на том факте, что число кратно 9 тогда, и только тогда, когда его цифры в сумме дают кратное 9. Так как 1 + 0 + 8 + 9 = 18 кратно 9, значит и 1089 кратно 9. Таким образом, 1089 при умножении на любое целое число даст кратное 9. И раз уж прозвучавшие цифры в сумме дают 29, и следующее кратное 9, которое больше 29, это 36, то наш доброволец должно быть не учёл число 7 (так как 29 + 7 = 36). Есть более утончённые способы заставить добровольца в конечном итоге прийти к кратному 9. Вот некоторые из моих любимых:
Пусть он наугад выберет шестизначное число, перемешает его цифры, затем отнимет меньшее из шестизначных чисел из большего. Так как мы производим вычитание двух чисел с одинаковой модульной суммой (в самом деле, сумма цифр идентична), полученная в итоге разница будет иметь модульную сумму в размере 0, и, следовательно, число будет кратно 9. Далее продолжайте как и раньше, чтобы найти недостающую цифру.
Пусть он тайно выберет четырёхзначное число, перевернёт его задом наперёд, а потом вычтет меньшее из чисел из большего. (получится кратное 9) Затем пусть умножит полученное число на 3, а вы продолжайте как и раньше.
Попросите его умножать цифры друг на друга до тех пор, пока их произведение не превратится в семизначное число. Это будет не «гарантированное» кратное 9, но на практике так получается не меньше, чем в 90% случаев (шансы высоки, что перемножаемые цифры будут включать 9-ки или две 3-ки, или две 6-ки, или 3 и 6). Я часто использую данный способ, когда выступаю перед математически продвинутой аудиторией, которая может раскусить другие методы.
Существует кое-какая проблема, за которой нужен глаз да глаз. Предположим, прозвучавшие числа в сумме дают кратное 9 (скажем, 18). После такого у вас не будет возможности определить, пропущен ли 0 или 9. Как исправить это? Легко - сжульничайте! Просто скажите:
«Вы ведь не пропустили 0, не так ли?» Если был пропущен 0, то вы успешно провернули свой трюк. Если нет, то скажите: «Оу, просто казалось, будто в голове у вас пусто! Вы не пропустили один, два, три или четыре, не так ли?» Доброволец либо покачает головой, либо скажет «нет». Затем вы продолжаете: «Как и не пропустили вы пять, шесть, семь или восемь. Вы не включили девять, не так ли?» Доброволец ответит утвердительно, и вы получите ваши заслуженные аплодисменты!
Сложение-чехарда
Данный приём сочетает в себе быстрые ментальные вычисления и поразительные предсказания. Вручите зрителю карту с десятью линиями на ней, пронумерованными от 1 до 10. Пусть зритель загадает два положительных числа от 1 до 20 и подпишет ими линии 1 и 2.
Далее попросите его записать сумму 1 и 2 линий на линии 3. Затем сумму линии 2 и 3 на линии 4, и так далее, как проиллюстрировано ниже.
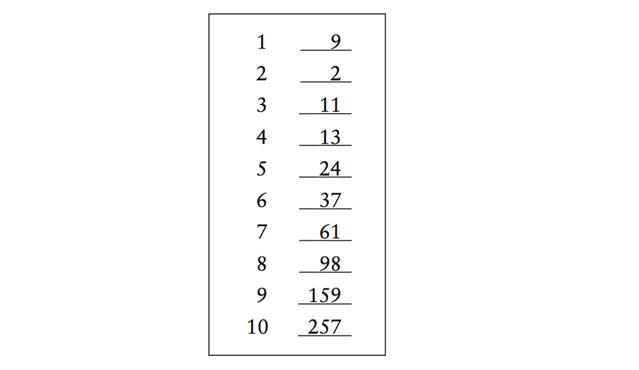
Наконец зритель показывает вам карту. Вы сразу же можете сказать ему сумму всех чисел на карточке. Например, в нашем случае, вы могли бы мгновенно объявить, что числа в сумме дают 671, даже быстрее, чем зритель сделал бы это с калькулятором. В качестве
«нежданчика», вручите зрителю калькулятор и и попросите его разделить число на линии 10 на число с линии 9. В нашем примере, частное 257/159 = 1,616. Пусть он озвучит первые три цифры частного, а после перевернёт карточку (там вы уже написали своё предсказание). Зритель будет очень удивлён тому, что вы уже записали число 1,61!
Почему это работает
Для проведения быстрых вычислений вам просто нужно умножить число с линии 7 на 11. Здесь 61 х 11 = 671. Причина, по
|
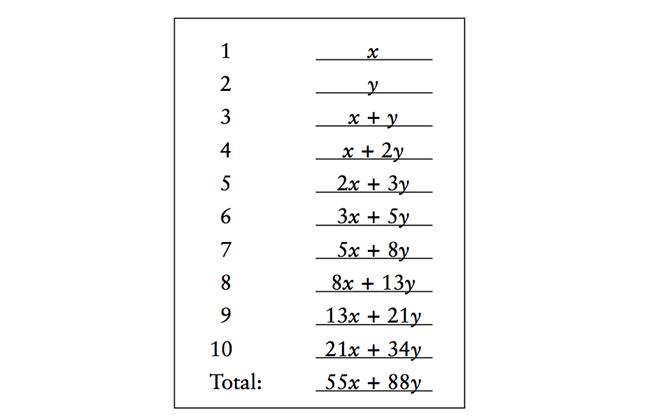
Что касается предсказания, мы используем тот факт, что для любого положительного числа (a, b, c, d), если a/b < c/d, дробь, которую вы получите путём «ошибочного сложения дробей» (например, сложение числителей и сложение знаминателей), будет находиться между двумя исходными дробями. То есть,
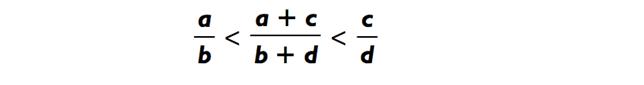
Таким образом, частное линии 10, делённой на линию 9, (21х + 34у)/(13х + 21у), должно лежать между
Следовательно, пропорция должна начинаться с цифр 1,61, как и было предсказано.
По сути, если вы продолжите такую «чехарду» вплоть до бесконечности, отношение последовательно идущих значений будет подбираться все ближе и ближе к
числу с таким огромным количеством удивительно красивых и загадочных свойств, что его часто называют золотое отношение (золотое сечение).
Магичиские квадраты
Вы готовы к испытанию совершенно другого порядка? Ниже вы найдёте то, что называют «магичиский квадрат». Столько всего было написано на данную тему и о том, как составлять их (вплоть до времен Древнего Китая). Здесь мы описываем способ презентации магических квадратов в развлекательном стиле. Вот заученная схема, которую я исполнял годами.
Я показываю визитку со следующей надписью на задней стороне:
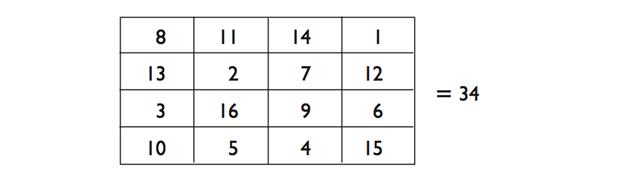
Я говорю : «Это называется магический квадрат. По сути, это самый маленький магический квадрат, который вы можете создать, используя числа от одного до шестнадцати. Вы заметите, что каждая строка и каждый столбец при сложении всех элементов дают одно и то же число - тридцать четыре. Сейчас, когда я провёл такое обширное исследование на тему магических квадратов, я предлагаю создать один для вас прямо у вас на глазах».
Затем я прошу кого-либо из аудитории дать мне любое число больше 34. Давайте предположим, что мне назвали 67.
|
Я продолжаю: «В случае с первым магическим квадратом, каждая строка и каждый столбец при сложении давали тридцать четыре. (на данной стадии, я обычно откладываю карточку с этим квадратом в сторону) Давайте посмотрим, что у нас получилось с новым квадратом». После проверки того, что кадая строка и каждый столбец в сумме равняются 67, я говорю: «Но я не останавливаюсь на этом. Специально для вас, я решил зайти ещё на один шаг дальше. Обратите внимание, обе диагонали при сложении дают шестьдесят семь!» Затем я указываю, что четыре квадратика в левом верхнем углу
в сумме дают 67 (16 + 19 + 22 + 10 = 64), как и все остальные строки и столбцы такого размера! «Они все в сумму равны шестидесяти семи. Но не верьте мне наслово. Пожалуйста, оставьте себе магический квадрат в качестве сувенира от меня и проверьте его потом сами!»
Почему это работает
Причина, по которой данный метод работает, основана на том факте, что каждая строка, столбец, диагональ из изначально
показанного магического квадрата при сложение даёт 34. Предположим, заданное число 82. Так как 82 - 34 = 48 (и 48/4 = 12), мы будет прибавлять 12 к каждому числу в квадратике. Затем каджая
«группа четвёрок», которая до этого равнялась 34, будет при сложении давать 34 + 48 = 82. Рассмотрите магический квадрат ниже.
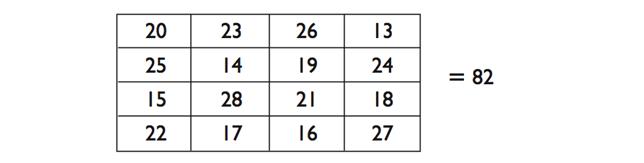
С другой стороны, если заданное число было бы 85, наши магические числа были бы 12 и 15. Так что нам мы бы прибавляли на 3 больше к квадратикам, которые содержат числа 13, 14, 15 и 16. Так как каждая строка, столбец и группа четвёрок содержит в точности одно из этих чисел, каждая группа четвёрок теперь будет при сложении давать 34 + 48 + 3 = 85, как в следующем магическом квадрате.
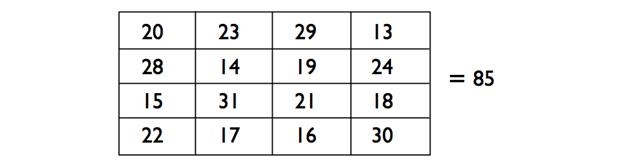
В качестве интересного матемагического пустячка, позвольте мне отметить еще одно удивительное свойство знаменитого магического квадрата 3-на-3 ниже.
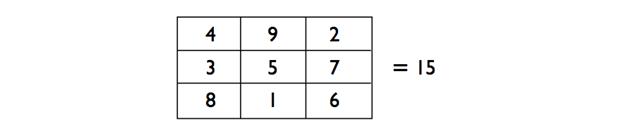
Не только строки, столбцы и диагонали суммируются до 15, но если вы представите строки магического квадрата как трёхзначные числа, то сможете удостовериться на калькуляторе, что 4922 + 3572 + 8162 = 2942 + 7532 + 6182. Также 4382 + 9512 + 2762 = 8342 + 1592 + 6722. Если вам
любопытно, почему так происходит, вы возможно захотите изучить мою статью «В самом деле «магические» квадраты!»
Быстрые кубические корни
Попросите кого-нибудь выбрать двузначное число и сохранить его в секрете. Затем попросите его возвести число в куб, то есть умножить его само на себя дважды (используя калькулятор). Например, если секретное число 68, пусть доброволец посчитает 68 х 68 х 68 = 314 432. Затем попросите его сказать вам ответ. Как только он назовёт вам куб, 314 432, вы можете мгновенно раскрыть секрет исходного числа - кубический корень, 68. Как?
Чтобы рассчитывать кубические корни, вам нужно выучить кубы чисел от 1 до 10:
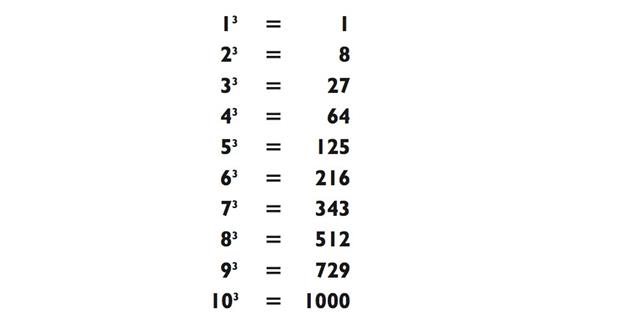
Как только вы выучите эти значения, расчёт кубических корней станет таким же лёгким, как назвать значение числа π . Например, в данном случае:
Упрощенные квадратные корни
Квадратные корни также могут быть легко посчитаны, если вам задали полный квадрат. Например, если кто-то сказал вам, что квадрат двузначного числа будет 7569, то вы в состоянии мгновенно ответить, что исходное число (квадратный корень) это 87. Вот как:
◆ Посмотрите на величину сотен (цифры, предшествующие
последним двум), 75 в данном примере
◆ Так как 75 находится между 82 (8 х 8 = 64) и 92 (9 х 9 = 81), то нам известно, что квадратный корень будет где-то в районе 80>. Следовательно, первая цифра квадратного корня будет 8. Существует два числа, чьи квадраты заканчиваются на 9: 32 = 9, 72 =
49. Так что последня цифра должна быть 3 или 7. Таким образом, квадратный корень либо 83, либо 87. Какой из них?
◆ Сравните исходное число с квадратом 85 (который мы можем
легко посчитать как 80 х 90 + 25 = 7225). Так как 7569 больше, чем
7225, квадратный корень будет большим числом, 87.
Давайте решим ещё один пример.
Удивительная сумма
Следующий трикс впервые был показан мне Джеймсом
«Удивительным» Рэнди, который его эффективно использовал в своей магии. Здесь волшебник может предсказать сумму четырёх случайно выбранных трёхзначных чисел.
Дабы подготовить данный фокус, вам понадобятся три комплекта колод из девяти карт каждая и кусок бумаги с записанным числом 2247 на нём, который вы запечатаете в конверт. Далее, над каждым комплектом карт произведите следующие действия:
★ На колоде А запишите следующие цифры (одно на каждую
карту):
★ На колоде В запишите следующие числа:
★ На колоде С запишите следующие числа:
Выбирете трёх человек из аудитории и дайте каждому колоду карт. Пусть каждый из ваших добровольцев наугад выберет одну из девяти карт, которые они держат в руках. Допустим, они выбрали числа 4286, 5792 и 5435. Теперь, соблюдая последовательность, пусть каждый громко назовёт одну из цифр четырёхзначного числа: сначала человек А, потом человек В и, наконец, человек С. Скажем, они
назвали цифры 8, 9 и 5. Запишите цифры 8, 9 и 5 (895) и скажите: «Вы должны признать, что данное число было выбрано полностью наугад и не могло быть возможности заранее предсказать его».
Далее, пусть три человека выкрикнут другие цифры со своих карт. Скажем, были названы 4, 5 и 3. Запишите 453 ниже числа 895. Затем повторите данную процедуру ещё два раза для двух оставшихся чисел, получив в итоге четыре трёхзначных числа, что-то вроде:
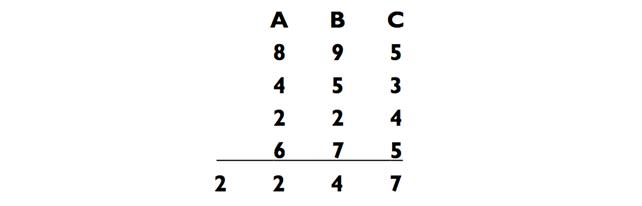
После пусть кто-нибудь сложит эти четыре числа и озвучит сумму. А дальше пусть кто-нибудь откроет конверт, дабы показать ваше предсказание. Наслаждайтесь аплодисментами!
Почему это работает
Взгляните на числа на картах каждой из колод и посмотрите, сможете ли вы найти каку-либо последовательность. Каждый набор чисел в сумме даёт одинаковую величину. Набор чисел А при сложении даёт 20. Набор В - 23. Набор С - 17. С цифрами из колоды
«С», которые в правом столбике дают в сумме 17, вы всегда будете записывать 7 и переносить 1. С числами из колоды «В», которые в сумме дают 23 (плюс 1), вы всегда будете записывать 4 и переносить 2. Наконец, с числами из колоды «А», которые в сумме дают 20, после прибавления 2 вы получите общий итог 2247!
День для любой даты
Мы завершим нашу книгу одним из проверенных временем подвигов ментальных калькуляций: как узнать на какой день недели приходится чей-либо день рождения. Это действительно очень практичный навык. Не каждый денькто-то будет просить вас возвести в квадрат трёхзначное число, но едва ли один день проходит без того, что кто-то упоминает дату из прошлого или будущего. Всего лишь немного практики, и вы сможете быстро и легко определять день недели практически любой исторической даты. Сначала мы присвоим кодовый номер каждому дню недели. Их легко запомнить:
| ПОНЕДЕЛЬНИК | ВТОРНИК | СРЕДА | ЧЕТВЕРГ | ПЯТНИЦА | СУББОТА | ВОСКРЕСЕНИЕ |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 или 0 |
Далее нам понадобится код для каждого месяца. Коды будут использоваться для каждого года за двумя исключениями. Во время високосного года (например, 2000-2004-2008 и так далее) код месяца для Января будет 5, а для Февраля 1.
| Январь | Февраль | Март | Апрель | Май | Июнь | Июль | Август | Сентябрь | Октябрь | Ноябрь | Декабрь |
| 6 (5) | 2 (1) | 2 | 5 | 0 | 3 | 5 | 1 | 4 | 6 | 2 | 4 |
Теперь давайте вычислим день недели для любой даты в 2006 году. После этого, мы опишем 2007, затем 2008, и так далее, до конца вашей жизни. Когда все даты из будущего будут разобраны, мы сможем заглянуть назад в прошлое и определить дни недели для любой даты из 1900-ых или любого другого века.
Каждому году присвоен кодовый номер, и в случае 2006 года таковым будет 0 (см. страницу).
Теперь, чтобы вычислить день недели, вы просто складываете код месяца плюс код даты плюс код года. Таким образом, для 3 Декабря 2006 года, мы рассчитываем
Код месяца + Дата + Код года = 4 + 3 + 0 = 7
Следовательно, эта дата приходится на День 7, что есть Воскресенье.
Как на счёт 18 Ноября 2006? Так как Ноябрь имеет код месяца 2,
мы имеем
Код месяца + Дата + Код года = 2 + 18 + 0 = 20
Теперь, раз уж неделя повторяется каждые семь дней, мы можем отнять любое кратное 7 от нашего ответа (7, 14, 21, 28, 35, . . .) и это никак не повлияет на день недели. Итак, наше заключительное действие представляет собой вычитание наибольшего кратного 7, чтобы получить 20 - 14 = 6. Следовательно, 18 Ноября 2006 года выпадает на Субботу.
Как на счёт 2007? Ну, что происходит с днём вашего рождения, когда вы переходите от одного года к следующему? Большинство из них состоит из 365 дней, и, так как 364 кратно 7 (7 х 52 = 364), то день недели вашего рождения передвинется вперёд на один (в случаях, когда 1 год = 365 дней). Если между вашими днями рождения 366 дней, тогда день недели вашего рождения передвинется на два вперёд. Следовательно, для 2007 года мы вычислили день недели как и раньше, но сейчас мы использовали код года 1. Далее, 2008 - високосный год. (Високосный год приходится на каждый четыре года, так что 2000, 2004, 2008, 2012, . . . , 2096 - високосные года двадцать первого века) Отсюда, для 2008, код года увеличивается на два, так что он теперь будет 3. Следующий год, 2009, не является високосным, так что код увеличивается на 1 (и будет 4).
Таким образом, 2 Мая 2007 года, например, будет
Код месяца + Дата + Код года = 0 + 2 + 1 = 3
так что эта дата приходится на Среду.
Для 9 Сентября 2008 года мы имеем
Код месяца + Дата + Код года = 4 + 9 + 3 = 16
Отнимая наибольшее кратное 7, мы получаем 16 - 14 = 2, так что дата приходится на Вторник.
С другой стороны, 16 Января 2008 года - високосный период, так что код месяца будет 5, вместо 6. Мы имеем
Код месяца + Дата + Код года = 5 + 16 + 3 = 24
и вследствие этого приходится на день 24 - 21 = 3, который является Средой. Для справки, мы перечислили все коды для каждого года двадцать первого века на рисунке на следующей странице. Хорошая новость заключается в том, что вам не нужно запоминать данную таблицу. Мы может устно посчитать код года для любой даты в промежутке от 2000 до 2099. Для определения кода 2000 + x, мы просто берём число х/4 (игнорируя остаток) и прибавляем частное к х. Код года может быть сокращён путём вычитания из него кратного 7. Например, в случае с 2061, мы видим, что 61/4 = 15 (с остатком 1, который мы не учитываем). Таким образом, 2061 имеет код года в размере 61 + 15 = 76. И раз уж мы можем отнять любое кратное 7, то давайте используем упрощённый код года в виде 76 - 70 = 6.
Феноменов , как и старое ?
Скептики ВИЧ-СПИДа утверждают, что образ жизни, а не ВИЧ, вызывает СПИД. Тем не менее, чтобы сделать такое утверждение, они должны проигнорировать конвергенцию доказательств в поддержку ВИЧ как причину переноса инфекции СПИД, и одновременно проигнорировать такое очевидное свидетельство как серьёзная зависимость между ростом распространения СПИДа среди больных гемофилией, вскоре после того, как ВИЧ по невнимательности был внесён в систему кровоснабжения. Вдобавок к этому, их альтернативная теория и близко не объясняет такое количество фактов, как теория ВИЧ.
СЕКРЕТЫ МЕНТАЛЬНОЙ МАТЕМАТИКИ
|
|
Мгновенное умножение
Давайте начнём с одного из моих любимых подвигов устной математики: как умножать в уме любое двузначное число на 11. Это очень легко, если вы знаете секрет.
Представьте следую задачу:
Х 11
Для решения данной задачи нужно просто сложить цифры, 3 + 2
= 5, а затем поместить 5-ку между 2-ой и 3-ой. Вот и ваше решение:
352
Что может быть легче? Теперь попробуйте:
Х 11
С тех пор, как 5 + 3 = 8, ответ достаточно простой:
583
Ещё пример. Не подглядывая и ничего не записывая, чему будет равно:
Х 11?
У вас получилось 891? Поздравляю!
Пока вы ещё не через чур воодушевились: я показал вам лишь половину того, что необходимо знать. Допустим задача следующая:
Х 11
Несмотря на то, что 8 + 5 = 13, ответ НЕ 8135!
Как и прежде, цифра 3 ставится между, но 1 добавляется к цифре 8 для получения правильного ответа: 935
Представляйте задачу следующим образом:
Вот ещё пример. Попробуйте 57 х 11.
Так как 5 + 7 = 12, решением будет:
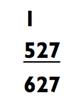
Так, теперь ваша очередь. Как можно быстрее, сколько будет
77 х 11?
Если вы получили ответ 847, то можете похлопать себя по спине.
Вы на пути к превращению в матемага.
Я знаю по опыту, что если вы скажете другу или учителю, что можете в уме умножить любое двузначное число на 11, просьба умножить 99 на 11 не заставит себя долго ждать. Так давайте сделаем это прямо сейчас, чтобы вы были готовы.
Раз уж 9 + 9 = 18, то ответ:
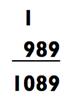
Хорошо попрактикуйте свой новый навык какое-то время, а затем начинайте выпендриваться. Вы будете удивлены тому, какую реакцию это вызовет. (раскрывать или нет свои секреты - решайте сами!)
Добро пожаловать назад. К этому моменту у вас, должно быть, появилось несколько вопросов, таких как:
«Можем ли мы использовать данный метод для умножения трёхзначных (или больше) чисел на 11?»
Безусловно. Например, для задачки 314 х 11 ответ всё ещё будет начинаться с 3 и заканчиваться на 4. Так как 3 +1 = 4, а 1 + 4 = 5, ответ будет 3454. Но мы отложим задачи посерьёзнее напотом.
Вероятнее всего, вы должно быть спрашиваете себя:
«Ну, это хорошо, что можно умножать на 11. Но как на счёт больших цифр? Как умножить цисла на 12, 13 или 36?»
Мой ответ на это: ТЕРПЕНИЕ! Об этом рассказано дальше в книге. В главах 2, 3, 6 и 8 вы изучите методы умножения, позволяющие перемножать любые 2 числа. А ещё лучше то, что вам не придётся запоминать специальные правила для каждого случая. Пригоршня методов - вот всё, что вам понадобится для умножения чисел в уме быстро и с лёгкостью.
Дата: 2018-12-21, просмотров: 669.
