Работа по учебнику (раздел «Мозаика заданий»).
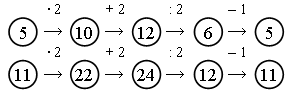
Задание 1. Вычислите по цепочке.

Задание 2. Посчитайте сумму на чеке.
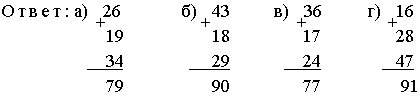
Задание 3. Какой домик выше и на сколько?
а) 23 + 18 = 41 (м) – 1-й дом. в) 17 + 26 = 43 (м) – 1-й дом.
37 + 9 = 46 (м) – 2-й дом. 8 + 37 = 45 (м) – 2-й дом.
46 – 41 = 5 (м) – на столько 45 – 43 = 2 (м) – на столько
выше 2-й дом. выше 2-й дом.
б) 12 + 29 = 41 (м) – 1-й дом. г) 8 + 16 + 25 = 49 (м) – 1-й дом.
18 + 22 = 40 (м) – 2-й дом. 16 + 16 + 17 = 49 (м) – 2-й дом.
41 – 40 = 1 (м) – на столько Высота домов одинаковая.
выше 1-й дом.
Задание 4. Восстановите задачи и решите их.
а) Всего – 96 км Решение:
Проехали – 37 км и 36 км 1) 37 + 36 = 73 (км) – проехали.
Осталось – ? км 2) 96 – 73 = 23 (км) – осталось.
б) Всего – 84 км Решение:
Проехали – 27 км и 28 км 1) 27 + 28 = 55 (км) – проехали.
Осталось – ? км 2) 84 – 55 = 29 (км) – осталось.
в) Всего – ? км Решение:
1-я и 2-я машины – 64 км 1) 64 – 23 = 41 (км) – 1-я машина.
2-я машина – 23 км 2) 56 – 23 = 33 (км) – 3-я машина.
2-я и 3-я машины – 56 км 3) 41 + 23 + 33 = 97 (км) – всего.
г) Всего – 94 км Решение:
1-я машина – 66 км 1) 66 + 57 = 123 (км) – проехали
2-я машина – 57 км обе машины вместе.
Проехали после встречи – ? км 2) 123 – 94 = 29 (км) – между
машинами.
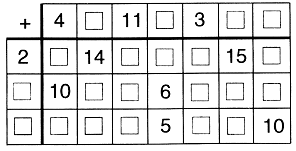
Задание 5. В сумме должно быть 100. Какое число в пустой клетке?
Ответ:
а) 100 – 23 – 18 – 27 – 5 = 27 в) 100 – 9 – 26 – 25 – 17 = 23
б) 100 – 19 – 24 – 33 – 8 = 16 г) 100 – 31 – 29 – 15 – 7 = 18
Задание 6. Сумма должна равняться 66. Какую плитку надо убрать?
Ответ:
а) 12 + 15 + 17 + 13 + 26 = 83 в) 18 + 9 + 21 + 18 + 19 = 85
83 – 66 = 17 85 – 66 = 19
б) 22 + 23 + 7 + 24 + 14 = 90 г) 22 + 8 + 9 + 25 + 27 = 91
90 – 66 = 24 91 – 66 = 25
Урок 67
Смысл действия умножения
Цели деятельности учителя: создать условия для понимания смысла действия умножения; способствовать формированию понятия о том, что знак умножения используется для записи суммы одинаковых слагаемых, развитию умения решать текстовые задачи, записывать равенства с помощью знака умножения.
Планируемые результаты образования.
Предметные: имеют представление о том, как используется знак умножения для записи суммы одинаковых слагаемых; знают, что вычисление чисел производят с помощью сложения; умеют записывать решение задачи двумя способами (используя сложение и умножение), восстанавливать пропущенные числа в равенствах, проверять верность записанных равенств, наблюдать за переместительным свойством умножения.
Личностные УУД: понимают ценность человека как разумного существа, стремящегося к познанию мира и самосовершенствованию; имеют адекватное представление о школе, об учении и поведении в процессе учебной деятельности; могут объяснить, для чего нужно изучать математику, где пригодятся эти знания; испытывают желание оказания помощи в обучении товарища.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: определяют и формулируют цель деятельности на уроке с помощью учителя; высказывают свое предположение на основе работы с учебником; контролируют свои действия; познавательные: ориентируются в своей системе знаний; отличают новое от уже известного с помощью учителя; добывают новые знания, находят ответы на вопросы, используя учебник, иллюстрации, свой жизненный опыт, информацию, полученную на уроке; перерабатывают полученную информацию; делают выводы в результате совместной работы всего класса; коммуникативные: доносят свою позицию до всех участников образовательного процесса; оформляют свою мысль в устной и письменной речи; слушают и понимают речь других (одноклассников, учителя); решают поставленную задачу.
Ход урока
I. Устный счет.
1. Найдите слагаемые и значения сумм.
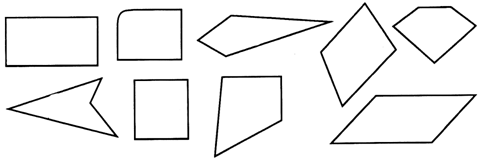
2. Чего на чертеже больше – четырёхугольников или прямоугольников? На сколько больше?
3. «Сколько девочек в вашем классе?» – спросил Игорь у Коли. Коля, немного подумав, ответил: «Если отнять от наибольшего двузначного числа число, записанное двумя семёрками, и от полученного результата отнять наименьшее двузначное число, то получится столько, сколько девочек в нашем классе». Сколько же девочек в классе, где учится Коля?
4. Назовите пропущенные числа.
20, 21, 22, 23, … , … , … , 27, … , 29;
30, … , … , 33, … , 35, … , … , … , 39;
… , … , 42, … , … , … , 46, … , … , … ;
… , … , … , … , 54, … , … , … , … , … .
II. Сообщение темы урока.
– Прочитайте записи на доске:
5 + 3 + 9 5 + 5 + 5 3 + 8 + 4
– Какая запись является «лишней»?
– Сегодня на уроке будем работать с суммой, записанной одинаковыми слагаемыми.
III. Работа по учебнику.
Задание 1. Сколько рядов коробок? (4 ряда.)
– Сколько коробок в каждом ряду? (5 коробок.)
– Сколько всего коробок привезли в магазин?
5 + 5 + 5 + 5 = 20 4 + 4 + 4 + 4 + 4 = 20
– Сложение одинаковых чисел называется умножением. Знак умножения «·».
Сумму одинаковых чисел можно записать короче:
5 + 5 + 5 + 5 = 5 · 4.
Пять умножить на четыре.
4 + 4 + 4 + 4 + 4 = 4 · 5.
Четыре умножить на пять.
Задание 2. Выполните запись по образцу:
6 + 6 + 6 = 6 · 3 = 18
5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 5 · 10 = 50
2 + 2 + 2 + 2 + 2 = 2 · 5 = 10
9 + 9 + 9 + 9 = 9 · 4 = 36
– Прочитайте задачу 3. Что известно? Что требуется узнать? Выполните краткую запись и решите задачу. Запишите все суммы с помощью знака умножения.
а) Вера – 4 ш. по 3 р.
Галя – 6 ш. по 3 р.
Даша – 7 ш. по 3 р.
Решение: 1) 3 + 3 + 3 + 3 = 3 · 4 = 12 (р.) – заплатила Вера;
2) 3 + 3 + 3 + 3 + 3 + 3 = 3 · 6 = 18 (р.) – заплатила Галя;
3) 3 + 3 + 3 + 3 + 3 + 3 + 3 = 3 · 7 = 21 (р.) – заплатила Даша.
Задание 4. Какие суммы можно записать с помощью знака умножения?
8 + 8 = 8 · 2 = 16 6 + 6 = 6 · 2 = 12 7 + 7 = 7 · 2 = 14
– Прочитайте задачу 5. Что известно? Что требуется узнать? Запишите решение с помощью знака умножения.
1 день – 4 урока. Решение:
7 дней – ? уроков. 4 + 4 + 4 + 4 + 4 + 4 + 4 = 28 (ур.);
4 · 7 = 28 (ур.).
Задание 6. Выполните запись. (4 · 3 = 4 + 4 + 4 = 12.)
Задание 7. Выполните вычисления, записывая промежуточные результаты.
13 + 13 + 13 = 26 + 13 = 39.
20 + 20 + 20 + 20 +20 = 40 + 20 + 20 + 20 = 60 + 20 + 20 = 80 + 20 = 100.
25 + 25 + 25 + 25 = 50 + 25 + 25 = 75 + 25 = 100.
17 + 17 + 17 = 34 + 17 = 51.
– Составьте и решите задачу 8.
1-я корзина – 6 кг. Решение:
4 корзины – ? кг. 6 + 6 + 6 + 6 = 24 (кг);
6 · 4 = 24 (кг).
Задание 9 (работа в парах). Прибавляйте по очереди пятерки, пока не получится 100.
5 + 5 = 10 5 · 2 = 10
5 + 5 + 5 = 15 5 · 3 = 15
5 + 5 + 5 + 5 = 20 5 · 4 = 20
5 + 5 + 5 + 5 + 5 = 25 5 · 5 = 25
5 + 5 + 5 + 5 + 5 + 5 = 30 и т. д. 5 · 6 = 30 и т. д.
IV. Итог урока.
– Что нового узнали на уроке? Что называют умножением?
Урок 68
Перестановка множителей
Цели деятельности учителя: содействовать успешному усвоению понятий «множители», «произведение»; помочь практически освоить переместительное свойство умножения; создать условия для формирования навыков решения примеров с переместительным свойством умножения, нахождения площади фигур разными способами; способствовать развитию умений читать выражения, записывать сложение с помощью умножения, находить равные произведения.
Планируемые результаты образования.
Предметные: имеют представление о том, как используются понятия «множители», «произведение»; знают переместительное свойство умножения; умеют решать примеры с применением переместительного свойства умножения, находить площадь фигуры разными способами, равные произведения, записывать сложение с помощью умножения.
Личностные УУД: понимают значение знаний для человека и принимают его; адекватно оценивают собственную учебную деятельность.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: планируют решение учебной задачи, выстраивают алгоритм действий; корректируют деятельность, вносят изменения в процесс с учетом возникших трудностей; познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; формулируют ответы на вопросы учителя; коммуникативные: планируют цели и способы взаимодействия; обмениваются мнениями, слушают друг друга, понимают позицию партнера, в том числе и отличную от своей, согласовывают действия с партнером.
Ход урока
I. Устный счет.
1. Там, где возможно, поставьте знаки сравнения между числами (вместо  может стоять любая цифра).
может стоять любая цифра).
5  … 8
… 8  3
3  … 3
… 3  7
7  … 2
… 2 
 …
… 

2. Игорь ниже Вити. Коля выше Вити. Миша ниже Игоря. Назовите имена мальчиков с меньшего до высшего роста.
3. Винни-Пух сочинил 36 шумелок, 39 пыхтелок и 17 сопелок. Сколько всего песенок сочинил Винни-Пух?
4. Винни-Пух, Кролик и Пятачок собрали с огорода 16 кабачков, что на 7 больше, чем патиссонов. Сколько патиссонов собрали друзья?
II. Сообщение темы урока.
– Как называются числа при сложении? (Слагаемые, сумма.) 5 + 3 = 8.
– Как называются числа при вычитании? (Уменьшаемое, вычитаемое, разность.) 5 – 3 = 2.
III. Работа по учебнику.
Задание 1. Какие геометрические фигуры расположены в таблице? Сколько всего фигур?
– Объясните, как считал Коля. (В каждом ряду по 3 фигуры. Всего 5 рядов.) 3 + 3 + 3 + 3 + 3 = 3 · 5 = 15.
– Объясните, как считал Вася. (В каждом столбике по 5 фигур. Всего 3 столбика.) 5 + 5 + 5 = 5 · 3 = 15.
– Числа, которые перемножают, называют множителями. Результат умножения чисел называют произведением.
3 · 5 = 15 – произведение множители
– Рассмотрите вычисления Коли и Васи. Что вы заметили?
(3 · 5 = 5 · · 3.)
– При перестановке множителей произведение не меняется.
Задание 2. Сколько утят на картинке? Посчитайте двумя способами. Запишите суммы с помощью знака умножения.
4 + 4 + 4 = 4 · 3 = 12
3 + 3 + 3 + 3 = 3 · 4 = 12
Задание 3. Запишите сложение с помощью умножения.
4 + 4 + 4 + 4 + 4 = 4 · 5 = 20 7 + 7 + 7 = 7 · 3 = 21
5 + 5 + 5 + 5 = 5 · 4 = 20 3 + 3 + 3 + 3 + 3 + 3 + 3 = 3 · 7 = 21
Задание 4. Найдите звёздочки, на которых произведения равны.
3 · 9 = 3 · 9 5 · 9 = 9 · 5
3 · 6 = 6 · 3 7 · 4 = 4 · 7
5 · 9 = 9 · 5
– Прочитайте задачу 5. Что известно? Что требуется узнать? Выполните краткую запись и решите задачу.
Коля – 2 к. по 5 ор. Решение:
Вася – 5 к. по 2 ор. 1) 5 · 2 = 10 (ор.) – у Коли;
Всего – ? кг 2) 2 · 5 = 10 (ор.) – у Васи.
Задание 6. Найдите произведения с помощью сложения.
3 · 6 = 3 + 3 + 3 + 3 + 3 + 3 = 18.
3 · 20 = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 +
+ 3 + 3 + 3 = 60.
7 · 10 = 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 70.
4 · 7 = 4 + 4 + 4 + 4 + 4 + 4 + 4 = 28.
2 · 18 = 18 · 2 = 18 + 18 = 36.
Задание 7. Решение логических задач.
– Запишите число клеток в прямоугольниках разными способами.
6 + 6 + 6 + 6 = 6 · 4 = 24.
4 + 4 + 4 + 4 + 4 + 4 = 4 · 6 = 24.
3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 =3 · 11 = 33.
11 + 11 + 11 = 11 · 3 = 33.
– Вычислите площадь каждого прямоугольника.
– У какого прямоугольника площадь больше? На сколько больше?
Задание 8. Какие равенства верные, а какие нет?
5 + 7 = 7 + 5 – верно 5 · 7 = 7 · 5 – верно
4 + 8 = 8 · 4 – неверно 3 · 4 = 4 + 3 – неверно
IV. Работа по карточкам.
1. Запишите примером:
а) число 2 повторите слагаемым 4 раза;
б) число 3 повторите слагаемым 5 раз;
в) число 9 повторите слагаемым 3 раза;
г) число 45 повторите слагаемым 2 раза.
2. Сравните:
5 + 5 + 5 … 5 + 5 + 5 + 5
3 + 3 + 3 + 3 … 3 + 3 + 3
9 + 9 + 9 … 9 + 9
8 + 8 + 8 + 8 … 8 + 8 + 8 + 8 + 8
V. Итог урока.
– Как называются числа при умножении?
Урок 69
Использование действия умножения
при выполнении заданий
Цели деятельности учителя: способствовать формированию навыков использования знака умножения при записи суммы одинаковых слагаемых, перестановке множителей при вычислениях; создать условия для совершенствования умения восстанавливать равенства, решать текстовые задачи.
Планируемые результаты образования.
Предметные: имеют представление о том, как используется знак умножения для записи суммы одинаковых слагаемых; знают, что вычисление чисел производят с помощью сложения; умеют записывать решение задачи двумя способами (используя сложение и умножение), восстанавливать пропущенные числа в равенствах, проверять верность записанных равенств, наблюдать за переместительным свойством умножения, составлять задачи на нахождение произведения.
Личностные УУД: сохраняют мотивацию к учебной деятельности; проявляют интерес к новому учебному материалу.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: принимают и сохраняют учебную задачу; определяют и формулируют цель деятельности на уроке с помощью учителя; познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; формулируют ответы на вопросы учителя; коммуникативные: участвуют в коллективном обсуждении проблем; обмениваются мнениями, слушают друг друга, понимают позицию партнера, в том числе и отличную от своей, согласовывают действия с партнером.
Ход урока
I. Устный счет.
1. Назовите номера рамок, в которых изображены:
а) ломаные; в) многоугольники;
б) кривые линии; г) замкнутые линии.
2. Найдите и исправьте ошибки.
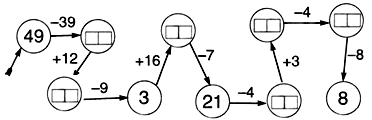
3. Барон Мюнхгаузен поймал 15 медведей, лисиц на 7 больше, а кабанов столько же, сколько лисиц. Сколько всего зверей поймал барон Мюнхгаузен?
4. Заполните пустые клетки «магического» квадрата.
| 26 | ||
| 20 | 21 | |
| 14 |
II. Работа по учебнику.
– Сегодня на уроке будем подсчитывать фигуры разными способами.
Задание 1. Сколько стульев на рисунке? (6.) Найдите общее число ножек. (4 · 6 = 6 · 4.)
– Прочитайте задачу 2. Что известно? Что требуется узнать?
11 + 11 + 11 + 11 = 11 · 4 = 44
Задание 3. Придумайте разные способы подсчёта фигурок на каждом рисунке.
5 + 5 + 5 + 5 = 5 · 4 = 20 4 + 4 + 4 + 4 + 4 = 4 · 5 = 20
3 + 3 + 3 + 3 = 3 · 4 = 12 4 + 4 + 4 = 4 · 3 = 12
2 + 2 + 2 + 2 = 2 · 4 = 8 4 + 4 = 4 · 2 = 8
Задание 4. Рассмотрите прямоугольник. Сколько умещается клеток в длине прямоугольника? (4 клетки.)
– Сколько умещается клеток в ширине? (3 клетки.)
– Сколько всего клеток?
3 + 3 + 3 + 3 = 4 + 4 + 4
3 · 4 = 4 · 3
12 = 12
– Объясните, что обозначают записи 4 · 3 и 3 · 4.
Задание 5. Выполните сложение. Запишите, если возможно, сложение чисел с помощью знака умножения.
24 + 24 = 48 = 24 · 2 16 + 16 + 16 = 48 = 16 · 3
37 + 37 = 74 = 37 · 2 15 + 15 + 15 + 15 = 60 = 15 · 4
64 + 46 = 110 29 + 29 + 21 = 79
Задание 6.
– Сколько барабанщиков в первой колонне? (5 · 7 = 35.)
– Сколько барабанщиков во второй колонне? (10 · 4 = 40.)
– Сколько всего барабанщиков? (35 + 40 = 75.)
– В какой колонне меньше барабанщиков? (Во второй.) На сколько меньше? (40 – 35 = 5.)
Задание 7.
– Вычислите сначала произведение. Затем прибавьте к нему число или отнимите число.
5 · 2 + 12 = 10 + 12 = 22 2 · 18 – 7 = 36 – 7 = 29
4 · 5 – 20 = 20 – 20 = 0 10 · 4 – 32 = 40 – 32 = 8
4 · 3 + 19 = 12 + 19 = 31 6 · 2 – 9 = 18 – 9 = 9
– Прочитайте задачу 3. Что известно? Что требуется узнать?
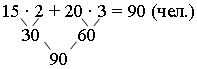
Задание 9. Восстановите пропущенные цифры.
4 · 7 = 7 · 4 9 · 2 = 9 + 9
3 · 5 = 5 · 3 12 = 6 · 2 = 2 · 6
3 · 2 = 3 + 3 2 · 7 = 2 + 12
III. Работа по карточкам.
1. Разбейте примеры на две группы. Запишите каждую группу в отдельный столбик. Вычислите.

2. В цветочном магазине продали 3 букета по 5 роз в каждом букете. Сколько цветов во всех букетах? Запишите решение.
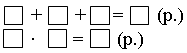
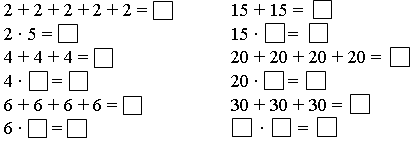
3. Замените сложение умножением.
Урок 70
Увеличение в 2 раза
Цели деятельности учителя: создать условия для формирования умений увеличивать числа вдвое и различать действия в случаях «увеличить на 2» и «увеличить в два раза» в текстовых задачах; способствовать формированию навыка самостоятельно придумывать задачу по данному решению, сравнивать числа и выражения.
Планируемые результаты образования.
Предметные: имеют представления о том, как записывать результат с помощью знака деления; умеют увеличивать числа (величины) вдвое, решать задачи на увеличение / уменьшение «на 2» и «в 2 раза», сравнивать результаты вычислений, делить на равные части, доказывать, составляя равенства, что умножение и деление – взаимно обратные действия.
Личностные УУД: понимают значение знаний для человека и принимают его; имеют адекватное представление о поведении в процессе учебной деятельности.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: определяют и формулируют цель деятельности на уроке с помощью учителя; умеют оценивать свою работу на уроке; познавательные: ориентируются в своей системе знаний; самостоятельно наблюдают над свойствами четных чисел; коммуникативные: планируют цели и способы взаимодействия; обмениваются мнениями, слушают друг друга, понимают позицию партнера, в том числе и отличную от своей, согласовывают действия с партнером.
Ход урока
I. Устный счет.
1. Проверьте, верно ли найден результат. Если нужно, исправьте его.
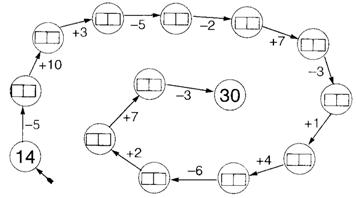
2. Три девицы под окном
Пряли поздно вечерком. (А. С. Пушкин.)
Старшая сестра напряла за вечер 20 граммов пряжи, средняя сестра на 8 граммов меньше, а младшая сестра – на 9 граммов больше, чем средняя. Сколько граммов пряжи напряла за вечер младшая сестра?
3. Кот учёный за день рассказал 16 волшебных сказок и 9 сказок о животных. До полудня он рассказал 12 сказок. Сколько сказок рассказал кот после полудня?
4. Пушки с пристани палят,
Кораблю пристать велят. (А. С. Пушкин.)
Всего прозвучало 8 выстрелов. Сколько было пушек, если каждая из них стреляла дважды?
II. Работа по учебнику.
Задание 1.
– Сколько пирожных съел Малыш? (3.) Сколько пирожных съел Карлсон? (Вдвое больше.) Что означает выражение «вдвое больше»? (Надо умножить на 2.)
3 + 3 = 3 · 2 = 6 (п.) – съел Карлсон.
Задание 2.
7 + 7 = 14 5 + 5 = 10 6 + 6 = 12
9 + 9 = 18 8 + 8 = 16 4 + 4 = 8
– Чем похожи эти суммы? Выполните умножение на 2.
7 · 2 = 14 5· 2 = 10 6 · 2 = 12
9 · 2 = 18 8 · 2 = 16 4 · 2 = 8
Задание 3. Восстановите записи.
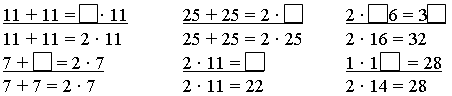
Задание 4.
– Сколько раз подтянулся Антон? (14 раз.) Сколько раз подтянулся Борис? (14 + 2 = 16 раз.) Сколько раз подтянулся Виктор? (14 · 2 = 28 раз.) Кто подтянулся больше всех?
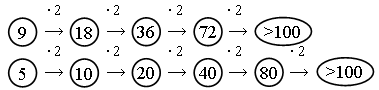
Задание 5 (работа в парах).
Задание 6. Поставьте знаки «>», «<» или «=» так, чтобы получилось верное равенство или неравенство.
8 · 2 … 16 19 · 2 … 19 2 + 2 … 2 · 2
16 · 2 … 16 35 · 2 … 80 34 · 2 … 34 + 2
16 · 2 … 34 42 · 2 … 80 2 + 29 … 29 · 2
Задание 7.
– Сколько грибов нашёл Антон? (12 грибов.) Сколько грибов нашёл Борис? (12 + 7 = 19 (гр.).) Сколько грибов нашёл Витя? (19 · 2 = 38 (гр.).) Сколько грибов нашли трое приятелей? (12 + 19 + 38 = 69 (гр.).) На сколько грибов меньше нашёл Антон, чем Витя? (38 – 12 = 26 (гр.).)
Задание 8. Составьте задачи и решите их.
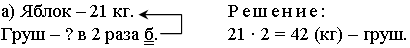
Задание 9. Учащиеся заполняют цепочки, прибавляя двойки.
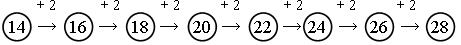
– Сколько шагов потребовалось, чтобы добраться до числа, вдвое большего, чем 14? (За 7 шагов.)
III. Работа по карточкам.
1. Составьте по рисункам произведения и найдите их значения:
а) б)


2. Ответьте на вопросы.
а) В пакете 3 кг картошки. Сколько картошки в 5 таких пакетах?
б) Сколько литров молока войдёт в 4 двухлитровые банки?
в) У жука 6 лапок. Сколько лапок у 3 жуков?
г) У паука 8 лапок. Сколько лапок у 5 пауков?
3. Сравните выражения:
36 · 3 … 36 + 3 29 · 2 … 30 + 30
17 · 4 … 17 + 17 + 17 8 · 5 … 8 + 8 + 8 + 8
IV. Итог урока.
– Что значит выражение «вдвое больше»?
Урок 71
знакомство с действием делением
Цели деятельности учителя: способствовать раскрытию смысла действия деления, знакомству со знаком деления; создавать условия для формирования навыка деления на 2, уменьшения числа вдвое; содействовать формированию умений решать задачи на время и текстовые задачи.
Планируемые результаты образования.
Предметные: имеют представления о том, как находить половину числа подбором, записывать результат с помощью знака деления; умеют увеличивать числа (величины) вдвое, решать задачи на увеличение / уменьшение «на 2» и «в 2 раза», сравнивать результаты вычислений, делить на равные части, доказывать, составляя равенства, что умножение и деление – взаимно обратные действия.
Личностные УУД: проявляют интерес к новому учебному материалу; применяют правила делового сотрудничества; сравнивают разные точки зрения.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: принимают и сохраняют учебную задачу; самостоятельно выделяют и формулируют цель; составляют план последовательности действий; познавательные: устанавливают причинно-следственные связи; воспроизводят по памяти информацию, необходимую для решения учебной задачи; коммуникативные: слушают и понимают речь других (одноклассников, учителя); решают поставленную задачу.
Ход урока
I. Устный счет.
1. Поставьте числа в пустых клетках так, чтобы суммы любых трёх чисел подряд были одинаковыми.
| 3 | 5 | 4 | |||||||||
| 7 | 8 | 4 | |||||||||
| 13 | 9 | 19 |
2. Назовите номера линий, которым подходят эти названия.
а) прямая: ___________; в) кривая: _____________;
б) ломаная: __________; г) замкнутая: __________.
3. В одной корзине 40 кг яблок, а в другой 15 кг. На сколько килограммов яблок меньше во второй корзине, чем в первой?
II. Сообщение темы урока.
– Рассмотрите записи на доске:
16 + 2 16 – 2 16 · 2 16 : 2
– Что означает каждое действие? Сегодня на уроке узнаем, как называется действие 16 : 2.
III. Работа по учебнику.
Задание 1. Сколько рыб поймал Вася? Сколько рыб Вася отдал кошке? (Половину.) Сколько рыб осталось у Васи? (6 + 6 = 12.)
– Мы разделили 12 пополам, то есть на 2. Это можно записать так: 12 : 2 = 6.
В результате получилось вдвое меньшее число.
Можно сказать, что мы уменьшили число в 2 раза.
Задание 2. Как разрезать каждый рисунок на две части так, чтобы в каждой оказалась половина фигурок?
14 : 2 = 7 24 : 2 = 12 16 : 2 = 8
В каких случаях это сделать невозможно? (15 : 2, 25 : 2.)
Задание 3. Сколько минут в половине часа? (60 : 2 = 30 (мин).) Сколько сантиметров в половине метра? (100 : 2 = 50 (см).) Сколько дней в половине апреля? (30 : 2 = 15 (дн.).) Придумайте похожие вопросы.
Задание 4. Выполните записи:
16 : 2 = 8 24 : 2 = 12 40 : 2 = 20
Задание 5. Выполните деление пополам с проверкой.
8 : 2 = 414 : 2 = 718 : 2 = 922 : 2 = 11
4 + 4 = 8 7 + 7 = 14 9 + 9 = 18 11 + 11 = 22
4 · 2 = 8 7 · 2 = 14 9 · 2 = 18 11 · 2 = 22
26 : 2 = 13 30 : 2 = 15
13 + 13 = 26 15 + 15 = 30
13 · 2 = 26 15 · 2 = 30
Задание 6. Сколько принес Вася? (16 грибов.) Сколько грибов обещал принести Коля? (16 · 2 = 32.) Сколько принес грибов Коля? (16 : 2 = 8.) На сколько меньше принес Коля грибов, чем обещал?
(32 – – 8 = 24.)
Задание 7 (работа в парах).
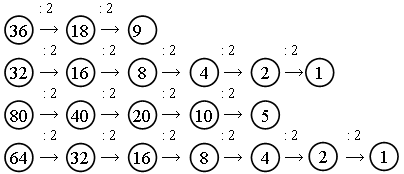
Задание 8. Выпишите числа, которые нельзя разделить пополам. (23, 35, 73, 37, 41.) Как они называются? (Нечетными.) Как называются числа, которые можно разделить пополам? (Четные.)
Задание 9. Задумайте число. Удвойте его. Прибавьте к результату 2. Разделите полученное число на 2. Отнимите 1. Какое число вы получили? (Нечетное число.)
IV. Фронтальная работа.
1. Заполните таблицу.
| Множитель | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Множитель | 5 | 3 | 8 | 6 | 4 | 9 | 7 | 2 |
| Произведение |
2. Запишите выражения и найдите их значения.
а) Из суммы чисел 47 и 18 вычесть 39.
б) Число 2 умножить на 6.
в) К разности чисел 80 и 27 прибавить 29.
3. Вдоль бортов яхты «Беда» висит 5 пар спасательных кругов. Сколько всего кругов висит вдоль бортов яхты?
4. Решите примеры:
17 – 9 + 8 32 + 32 – 47 + 77 – 69
14 – 5 + 7 27 + 33 – 24 + 59 – 72
V. Итог урока.
– Как найти половину числа?
Урок 72
ДЕЛение НА РАВНЫЕ ЧАСТИ
Цели деятельности учителя: способствовать рассмотрению деления на равные части; создавать условия для формирования навыка деления на равные части по рисунку; содействовать совершенствованию умения выполнять сложение нескольких слагаемых, делить отрезок на равные части.
Планируемые результаты образования.
Предметные: имеют представления о том, как находить половину числа подбором, записывать результат с помощью знака деления; умеют увеличивать числа (величины) вдвое, решать задачи на увеличение / уменьшение «на 2» и «в 2 раза», сравнивать результаты вычислений, делить на равные части, доказывать, составляя равенства, что умножение и деление – взаимно обратные действия.
Личностные УУД: анализируют и характеризуют эмоциональное состояние и чувства окружающих, строят свои взаимоотношения с их учетом.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: самостоятельно выделяют и формулируют цель; составляют план последовательности действий; познавательные: ориентируются в своей системе знаний; корректируют деятельность, вносят изменения в процесс с учетом возникших трудностей; коммуникативные: доносят свою позицию до всех участников образовательного процесса – оформляют свою мысль в устной и письменной речи; слушают и понимают речь других (одноклассников, учителя); решают поставленную задачу.
Ход урока
I. Устный счет.
1. На первой грядке выросло 16 кабачков, а на второй – на 4 кабачка больше.

– Соедините линией карточку с вопросом задачи и карточку с выражением для её решения.
2. Вставьте пропущенные знаки («+» и «–») так, чтобы получились верные равенства:
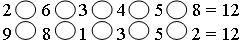
II. Сообщение темы урока.
– Рассмотрите фигуры на доске.
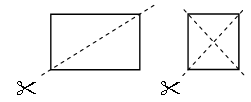
– На сколько равных частей разделили прямоугольник? На сколько равных частей разделили квадрат? Сегодня на уроке будем делить группу предметов на равные части.
III. Работа по учебнику.
Задание 1. Сколько мешков у разбойников? (15 мешков.) На сколько кучек они раскладывают эти мешки? (На 3 кучки.) Смогут ли разбойники разделить мешки поровну? Сколько мешков достанется каждому?
IV. Работа по карточкам.
– Прочитайте задачу 4. Что известно? Что требуется узнать? Выполните краткую запись и решите задачу.
1-й ряд ○ ○ ○ ○ ○
2-й ряд ○ ○ ○ ○ ○
3-й ряд ○ ○ ○ ○ ○
– Запишите результат деления. (15 : 3 = 5 (м.).) Проверьте себя сложением или умножением. (5 + 5 + 5 = 15; 5 · 3 = 15.)
Задание 2. Разделите каждый прямоугольник на две части так, чтобы количество фигурок в них было одинаково.
12 : 2 = 6 20 : 2 = 10

– Разделите эти же прямоугольники на 4 части с одинаковым количеством фигурок. Запишите равенства.

– На сколько ещё частей можно разделить каждый прямоугольник?
12 : 3 = 4 20 : 5 = 4
12 : 6 = 2 20 : 10 = 2
Задание 3. Возьмите 16 карандашей. Разделите их на 2 одинаковые кучки. Сколько карандашей в каждой кучке? (16 : 2 = 8 (к.).) Разделите карандаши на 8 одинаковых кучек. (16 : 8 = 2 (к.).)
Задание 4. Выполните деление. Проверьте себя сложением одинаковых чисел.
10 : 2 = 5 20 : 2 = 10 30 : 3 = 10 9 : 3 = 3
5 + 5 = 10 10 + 10 = 20 10 + 10 + 10 = 30 3 + 3 + 3 = 9 и т. д.
Задание 5. Разделите отрезок примерно пополам. Проверьте себя с помощью линейки. Измерьте длину отрезка и запишите равенство. 8 : 2 = = 4 (см); 4 + 4 = 8 (см).
– Разделите этот же отрезок на 4 равные части. 8 : 4 = 2 (см); 2 + 2 + + 2 + 2 = 8 (см).
– Начертите в тетради отрезок длиной 12 см. Разделите его на 3 одинаковые части. Разделите этот же отрезок на 6 одинаковых частей. Запишите равенства.
12 : 3 = 4 (см) 12 : 6 = 2 (см)
4 + 4 + 4 = 12 (см) 2 + 2 + 2 + 2 + 2 + 2 = 12 (см)
Задание 6. Выполните сложение.
10 + 10 + 10 + 10 + 10 = 10 · 5 = 50
18 + 18 + 18 = 18 · 3 = 54
23 + 23 + 23 + 23 = 23 · 4 = 92
8 + 8 + 8 + 8 + 8 = 8 · 5 = 40
Задание 7. Сколько квадратов на чертеже? (5 квадратов.) Сколько кустов надо высадить в каждый квадрат, чтобы растений было поровну? Ответ: 100 : 5 = 20 (к.).
– В центре посадили 60 кустов. Остальные высадили поровну в боковые квадраты. Сколько розовых кустов в каждом из них? Ответ: 100 – – 60 = 40 (к.); 40 : 4 = 10 (к.).
– В центральном квадрате посадили 60 растений рядами по 10. Сколько получилось рядов? Ответ: 60 : 10 = 6 (р.).
V. Фронтальная работа.
– Составьте выражения и найдите их значения.
а) Бабушка связала внукам 5 пар рукавиц. Сколько рукавиц связала бабушка внукам?
б) Купили 2 марки по 6 р., 2 марки по 4 р. и 2 марки по 9 р. Сколько денег заплатили?
в) Папа несёт 2 коробки по 8 кг, а Петя – 2 сетки по 3 кг. На сколько килограммов папин груз тяжелее?
г) Васе надо купить карандаш за 8 р. Он дал кассиру две 5-рублевые монеты. Сколько сдачи он получит?
VI. Итог урока.
– Как разделить предметы на равные части?
Урок 73
Деление – действие, обратное умножению
Цели деятельности учителя: способствовать раскрытию смысла действия деления (представление о делении как о действии, обратном умножению); создавать условия для формирования навыка умножения; содействовать совершенствованию умения составлять верные равенства из данных чисел, сравнивать и делать выводы.
Планируемые результаты образования.
Предметные: имеют представления о том, как находить половину числа подбором, записывать результат с помощью знака деления; умеют увеличивать числа (величины) вдвое, решать задачи на увеличение / уменьшение «на 2» и «в 2 раза», сравнивать результаты вычислений, делить на равные части, доказывать, составляя равенства, что умножение и деление – взаимно обратные действия.
Личностные УУД: применяют правила делового сотрудничества; сравнивают разные точки зрения; оценивают собственную учебную деятельность.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: планируют решение учебной задачи, выстраивают алгоритм действий; определяют и формулируют цель деятельности на уроке с помощью учителя; познавательные: привлекают информацию, полученную ранее, для решения учебной задачи; ориентируются в своей системе знаний; коммуникативные: участвуют в коллективном обсуждении проблем; обмениваются мнениями, слушают друг друга, понимают позицию партнера, в том числе и отличную от своей, согласовывают действия с партнером.
Ход урока
I. Устный счет.
1. Выполните действия.
48 + 30 – 26 = 54 + 45 – 80 = 5 + 44 + 30 =
90 – 6 – 43 = 20 + 69 – 37 = 65 – 22 + 27 =
97 – 26 + 20 = 30 + 43 – 52 = 78 – 54 + 24 =
80 – 31 – 20 =
2. Выполните действия и заполните таблицу.
| Слагаемое | 80 | 13 | 48 | 20 | 26 | 72 | 50 | 60 | |||||
| Слагаемое | 5 | 12 | 15 | 70 | 33 | 22 | 20 | 25 | 16 | 31 | 47 | ||
| Сумма | 37 | 69 | 90 | 80 | 40 | 70 | 80 |
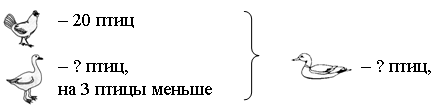
– Составьте задачу по краткой записи и решите ее.
II. Сообщение темы урока.
– Рассмотрите записи на доске:
□ + Δ = ○ 5 + 3 = 8
○ – □ = Δ 8 – 5 = 3
○ – Δ = □ 8 – 3 = 5
– Что обозначают эти записи? Как называют сложение и вычитание? (Взаимно обратными действиями.)
– Сегодня на уроке узнаем, можно ли умножение и деление назвать взаимно обратными действиями.
III. Работа по учебнику.
Задание 1. Сосчитайте двумя способами число кусочков в плитке шоколада. 5 + 5 + 5 + 5 = 20; 4 + 4 + 4 + 4 + 4 = 20.
– Запишите вычисления с помощью умножения. 5 · 4 = 20 или 4 · 5 =
= 20.
– Как разделить эту плитку между четырьмя детьми поровну? Нужно разделить её на 4 одинаковые части. (20 : 4 = 5.)
– А если детей пять? Сколько кусочков достанется каждому? (20 : 5 = = 4.)
Дата: 2018-12-21, просмотров: 579.