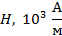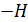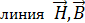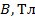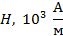Энергия магнитного поля
План решения задач
1. При анализе явления электромагнитной индукции (ЭМИ) в каждой конкретной задаче необходимо выяснять причину появления ЭДС индукции 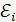 и индукционного тока. Согласно закону Фарадея:
и индукционного тока. Согласно закону Фарадея: 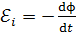 , – причиной появления ЭДС индукции является изменение магнитного потока
, – причиной появления ЭДС индукции является изменение магнитного потока 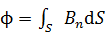 . Изменение магнитного потока может выполняться различными способами: а) изменением площади контура
. Изменение магнитного потока может выполняться различными способами: а) изменением площади контура 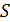 или площади
или площади 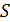 , которую описывает проводник при движении в магнитном поле; б) изменением проекции
, которую описывает проводник при движении в магнитном поле; б) изменением проекции 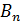 вектора магнитной индукции путем поворота контура; в) изменением величины магнитной индукции
вектора магнитной индукции путем поворота контура; в) изменением величины магнитной индукции  при перемещении постоянного магнита относительно контура или посредством изменения тока, создающего магнитное поле с индукцией
при перемещении постоянного магнита относительно контура или посредством изменения тока, создающего магнитное поле с индукцией  , и другими способами. Определение конкретной причины появления ЭДС индукции и индукционного тока позволяет определить его направление.
, и другими способами. Определение конкретной причины появления ЭДС индукции и индукционного тока позволяет определить его направление.
2. Направление индукционного тока в замкнутом проводнике определяют с помощью правила Ленца: индукционный ток  своим магнитным полем
своим магнитным полем 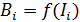 препятствует причине своего появления, т. е. тому изменению магнитного потока
препятствует причине своего появления, т. е. тому изменению магнитного потока 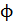 , которое вызвало появление ЭДС индукции и индукционного тока. Например, если магнитный поток
, которое вызвало появление ЭДС индукции и индукционного тока. Например, если магнитный поток 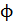 через площадь контура снижается, то магнитное поле индукционного тока
через площадь контура снижается, то магнитное поле индукционного тока 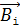 стремится поддержать неизменным магнитный поток, а для этого будет
стремится поддержать неизменным магнитный поток, а для этого будет 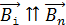 , – нормальной составляющей магнитной индукции, которая снижается. Правило Ленца трактуется и в более широком смысле: если причиной возникновения индукционного тока явилось движение магнита относительно проводящего контура или движение проводника в магнитном поле, то индукционный ток будет препятствовать движению, т. е. тормозить движущийся проводник путем отталкивания одноименных магнитных полюсов магнитных полей
, – нормальной составляющей магнитной индукции, которая снижается. Правило Ленца трактуется и в более широком смысле: если причиной возникновения индукционного тока явилось движение магнита относительно проводящего контура или движение проводника в магнитном поле, то индукционный ток будет препятствовать движению, т. е. тормозить движущийся проводник путем отталкивания одноименных магнитных полюсов магнитных полей 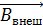 и
и 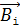 . Другой пример проявления правила Ленца наблюдаем в явлении самоиндукции: если ток в катушке индуктивности возрастает, например, при подключении в контур источника ЭДС, то при этом увеличивается собственное потокосцепление катушки; следовательно, индукционный ток
. Другой пример проявления правила Ленца наблюдаем в явлении самоиндукции: если ток в катушке индуктивности возрастает, например, при подключении в контур источника ЭДС, то при этом увеличивается собственное потокосцепление катушки; следовательно, индукционный ток  будет направлен противоположно току от внешнего источника ЭДС, чтобы препятствовать возрастанию тока; и наоборот, – при снижении тока в катушке индуктивности в ней появится индукционный ток
будет направлен противоположно току от внешнего источника ЭДС, чтобы препятствовать возрастанию тока; и наоборот, – при снижении тока в катушке индуктивности в ней появится индукционный ток  , сонаправленный снижающемуся току
, сонаправленный снижающемуся току 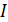 .
.
3. Отметим, что если движение проводника равномерное, то скорость изменения магнитного потока постоянна: 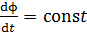 . В этом случае справедливо равенство
. В этом случае справедливо равенство 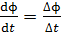 и для определения ЭДС индукции
и для определения ЭДС индукции 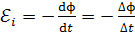 можно взять изменение магнитного потока
можно взять изменение магнитного потока 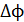 за конечный промежуток времени
за конечный промежуток времени 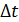 (см. задачу 47).
(см. задачу 47).
Задача 47. В однородном магнитном поле с индукцией 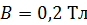 равномерно с частотой
равномерно с частотой 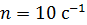 вращается медный стержень длиной
вращается медный стержень длиной 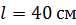 так, что плоскость его вращения перпендикулярна линиям магнитной индукции, а ось вращения проходит через один из концов стержня. Определите разность потенциалов
так, что плоскость его вращения перпендикулярна линиям магнитной индукции, а ось вращения проходит через один из концов стержня. Определите разность потенциалов 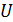 на концах стержня.
на концах стержня.
Дано Решение
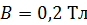 ; ;
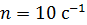 ; ;
 . .
|
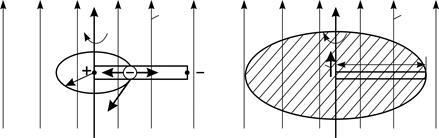
а б Рис. 79 |
Данную задачу можно решить одним из двух следующих способов.
Первый способ
В металлическом стержне имеются свободные электроны; рассмотрим один из них, движущийся со скоростью 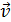 в магнитном поле (рис. 79 а). На электрон действует сила Лоренца:
в магнитном поле (рис. 79 а). На электрон действует сила Лоренца: 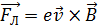 , где
, где 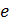 – заряд электрона;
– заряд электрона; 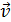 – линейная скорость его движения по окружности радиусом
– линейная скорость его движения по окружности радиусом 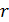 :
:
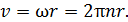
Модуль силы Лоренца
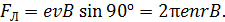 (1)
(1)
Направление силы Лоренца определим по правилу левой руки, располагая ладонь перпендикулярно плоскости рисунка. Полученное направление вектора силы, которая действовала бы на положительный заряд, изменяем на противоположное, так как электрон имеет отрицательный заряд. Силой Лоренца свободные электроны смещаются к точке 2 на конце стержня, удаленном от оси вращения (см. рис. 79 а). На другом конце стержня – в точке 1, вследствие недостатка свободных электронов, имеется избыточный положительный заряд ионов кристаллической решетки металла.
Избыточные заряды, сосредоточенные на концах стержня, создают электрическое поле с напряженностью 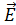 , направленной вдоль стержня. Это поле действует на свободные электроны электрической силой
, направленной вдоль стержня. Это поле действует на свободные электроны электрической силой
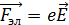 , (2)
, (2)
величина которой возрастает по мере накопления избыточных зарядов на концах стержня. Направление электрической силы противоположно силе Лоренца: 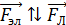 (см. рис. 79 а). Поэтому через достаточно малое время (
(см. рис. 79 а). Поэтому через достаточно малое время ( 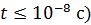 сумма этих сил
сумма этих сил 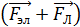 станет равна нулю и направленное движение электронов к концу вращающегося стержня прекратится. При этом на его концах будут находиться индуцированные заряды определенной величины и установится постоянная разность потенциалов между концами стержня:
станет равна нулю и направленное движение электронов к концу вращающегося стержня прекратится. При этом на его концах будут находиться индуцированные заряды определенной величины и установится постоянная разность потенциалов между концами стержня: 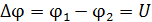 .
.
Запишем условие статического равновесия свободных электронов в металлическом стержне – 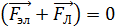 , которое означает равенство модулей этих сил:
, которое означает равенство модулей этих сил:
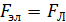 , или
, или 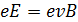 ;
; 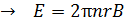 . (3)
. (3)
Напряженность электростатического поля 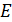 численно равна градиенту потенциала:
численно равна градиенту потенциала:
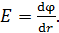 (4)
(4)
Приравняем значения напряженности 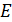 ЭСП в стержне по формулам (3) и (4) и выразим бесконечно малую разность потенциалов
ЭСП в стержне по формулам (3) и (4) и выразим бесконечно малую разность потенциалов 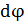 между точками стержня, находящимися на расстоянии
между точками стержня, находящимися на расстоянии 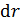 друг от друга:
друг от друга:
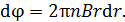 (5)
(5)
Определим разность потенциалов на концах стержня (между точками 1 и 2), суммируя элементарные значения 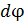 :
:
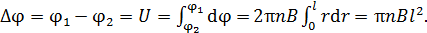 (6)
(6)
Вычислим разность потенциалов на концах стержня по формуле (6):
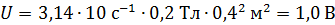 .
.
Второй способ
Используем закон Фарадея для электромагнитной индукции – ЭДС индукции 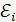 равна скорости изменения магнитного потока:
равна скорости изменения магнитного потока:
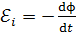 , (7)
, (7)
где 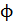 – магнитный поток через поверхность, которую описывает стержень при вращении:
– магнитный поток через поверхность, которую описывает стержень при вращении:
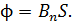 (8)
(8)
Здесь проекция вектора  на нормаль
на нормаль 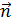 к описанной площади круга
к описанной площади круга  , так как вектор
, так как вектор 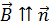 (рис. 79 б).
(рис. 79 б).
Стержень вращается равномерно, поэтому закон Фарадея (7) примет следующий вид:
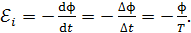 (9)
(9)
Здесь 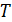 – период вращения стержня:
– период вращения стержня: 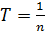 ; промежуток времени
; промежуток времени 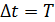 удобен тем, что стержень, совершая за период один оборот, описывает поверхность в форме круга площадью
удобен тем, что стержень, совершая за период один оборот, описывает поверхность в форме круга площадью 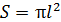 (см. рис. 79 б). С учетом этих замечаний и формулы (8) запишем закон ЭМИ (9) в виде:
(см. рис. 79 б). С учетом этих замечаний и формулы (8) запишем закон ЭМИ (9) в виде:
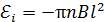 . (10)
. (10)
Так как стержень, в котором имеется ЭДС индукции, является неоднородным участком электрической цепи, запишем для него закон Ома в следующем виде:
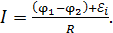 (11)
(11)
При постоянной скорости вращения устанавливается постоянная разность потенциалов на концах стержня, а ток в стержне 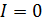 . Следовательно, согласно закону (11), получаем равенство
. Следовательно, согласно закону (11), получаем равенство
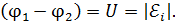 (12)
(12)
Учитывая выражение (10) для ЭДС индукции, преобразуем последнюю формулу в расчетную формулу разности потенциалов на концах стержня:
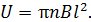
Эта формула совпадает с формулой, полученной выше первым способом.
Отметим, что первый способ позволил определить полярность напряжения (знаки потенциалов 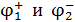 ), так как в нем рассмотрен механизм появления индуцированных зарядов на концах стержня посредством действия силы Лоренца на движущиеся со стержнем свободные электроны. Эта сила является сторонней силой
), так как в нем рассмотрен механизм появления индуцированных зарядов на концах стержня посредством действия силы Лоренца на движущиеся со стержнем свободные электроны. Эта сила является сторонней силой 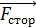 , благодаря действию которой возникает ЭДС индукции:
, благодаря действию которой возникает ЭДС индукции: 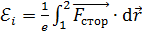 .
.
Задача 48. Рамка, содержащая 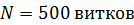 площадью
площадью 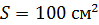 , вращается с частотой
, вращается с частотой 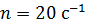 относительно оси
относительно оси 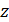 , совпадающей с диаметром рамки. Рамка находится в однородном поле с магнитной индукцией
, совпадающей с диаметром рамки. Рамка находится в однородном поле с магнитной индукцией 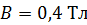 , которая направлена перпендикулярно оси вращения. Определите закон изменения ЭДС индукции
, которая направлена перпендикулярно оси вращения. Определите закон изменения ЭДС индукции 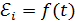 , максимальное значение ЭДС индукции
, максимальное значение ЭДС индукции 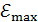 и направление индукционного тока
и направление индукционного тока  в момент времени
в момент времени 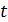 , соответствующий положению рамки, показанному на рис. 80.
, соответствующий положению рамки, показанному на рис. 80.
|
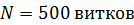 ; ;
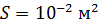 ; ;
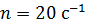 ; ;
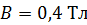 . .
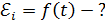 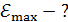 Направление
Направление 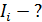
|
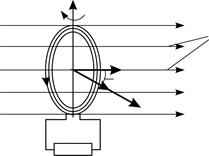
Рис. 80 |
Пусть в начальный момент времени 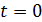 плоскость рамки была перпендикулярна линиям магнитного поля, а вектор
плоскость рамки была перпендикулярна линиям магнитного поля, а вектор 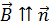 – нормали к плоскости рамки. Вращение рамки с постоянной частотой
– нормали к плоскости рамки. Вращение рамки с постоянной частотой 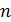 и с угловой скоростью
и с угловой скоростью 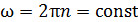 – равномерное. При этом угол поворота
– равномерное. При этом угол поворота 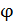 нормали
нормали 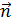 (см. рис. 80) изменяется с течением времени по закону
(см. рис. 80) изменяется с течением времени по закону 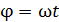 . Соответственно изменяется проекция на нормаль вектора магнитной индукции:
. Соответственно изменяется проекция на нормаль вектора магнитной индукции:
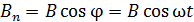 , (1)
, (1)
и полный магнитный поток через витки рамки, или потокосцепление ψ:
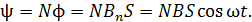 (2)
(2)
Электродвижущая сила индукции 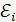 , возникающая в рамке при изменении ее потокосцепления по закону (2), определяется законом Фарадея:
, возникающая в рамке при изменении ее потокосцепления по закону (2), определяется законом Фарадея:
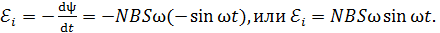 (3)
(3)
Согласно полученному уравнению (3), ЭДС индукции изменяется с течением времени по гармоническому закону.
Максимальное значение ЭДС индукции 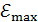 – амплитуда колебаний величины ЭДС, достигается периодически при
– амплитуда колебаний величины ЭДС, достигается периодически при 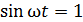 и, как следует из уравнения (3), определяется формулой
и, как следует из уравнения (3), определяется формулой
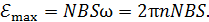 (4)
(4)
Вычислим величину 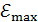 :
:
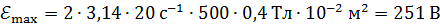 .
.
Если рамку замкнуть на внешнее сопротивление 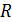 , то в ней потечет индукционный ток. К моменту времени
, то в ней потечет индукционный ток. К моменту времени 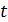 , как показано на рис. 80, рамка и нормаль к ней повернулись на угол
, как показано на рис. 80, рамка и нормаль к ней повернулись на угол 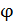 от начального положения нормали, в котором угол
от начального положения нормали, в котором угол 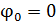 , а проекция
, а проекция  и потокосцепление
и потокосцепление 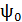 были максимальными. Согласно уравнению (2), величина потокосцепления
были максимальными. Согласно уравнению (2), величина потокосцепления 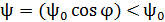 . Это уменьшение магнитного потока приведет к возникновению индукционного тока
. Это уменьшение магнитного потока приведет к возникновению индукционного тока  . Направление этого тока таково, чтобы создаваемое им магнитное поле с индукцией
. Направление этого тока таково, чтобы создаваемое им магнитное поле с индукцией 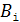 препятствовало бы уменьшению величин
препятствовало бы уменьшению величин 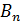 и потокосцепления
и потокосцепления 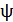 . Для этого необходимо, чтобы вектор
. Для этого необходимо, чтобы вектор 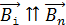 ; покажем на рис. 80 такой вектор
; покажем на рис. 80 такой вектор 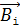 . Направление индукционного тока и создаваемое им магнитное поле
. Направление индукционного тока и создаваемое им магнитное поле 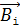 связаны правилом буравчика; ток
связаны правилом буравчика; ток  будет направлен против часовой стрелки.
будет направлен против часовой стрелки.
Через четверть периода вращения рамки угол 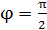 и величина
и величина 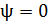 .
.
В течение второй четверти периода поворота рамки потокосцепление 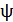 будет увеличиваться. Поле индукционного тока
будет увеличиваться. Поле индукционного тока 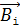 , препятствующее этому увеличению, имеет направление
, препятствующее этому увеличению, имеет направление 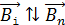 (это
(это 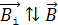 ), т. е. вектор
), т. е. вектор 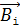 останется сонаправленным с нормалью
останется сонаправленным с нормалью 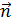 , так как индукция внешнего магнитного поля
, так как индукция внешнего магнитного поля 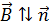 . В третьей четверти периода будет уменьшаться вектор
. В третьей четверти периода будет уменьшаться вектор 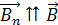 , при этом установится
, при этом установится 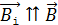 (согласно правилу Ленца), а индукционный ток изменит свое направление на противоположное. В связи с этим заметим, что согласно рассмотренной модели работает промышленный генератор переменного тока.
(согласно правилу Ленца), а индукционный ток изменит свое направление на противоположное. В связи с этим заметим, что согласно рассмотренной модели работает промышленный генератор переменного тока.
Задача 49. Проводящий стержень длиной 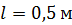 находится в однородном магнитном поле с индукцией
находится в однородном магнитном поле с индукцией 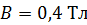 . Концы стержня замкнуты проводом, находящимся вне поля. Сопротивление всей цепи
. Концы стержня замкнуты проводом, находящимся вне поля. Сопротивление всей цепи 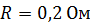 . Определите направление индукционного тока и мощность
. Определите направление индукционного тока и мощность 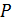 , необходимую для равномерного движения стержня со скоростью
, необходимую для равномерного движения стержня со скоростью 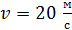 , направленной перпендикулярно линиям магнитной индукции.
, направленной перпендикулярно линиям магнитной индукции.
Дано Решение
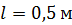 ; ;
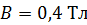 ; ;
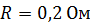 ; ;
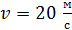 ; ;
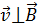 .
Направление .
Направление 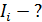
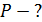
|
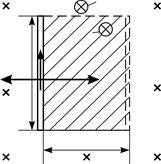
Рис. 81 |
При движении стержень пересекает линии магнитной индукции, и через площадь прямоугольника  , описанную проводником (рис. 81), имеется магнитный поток
, описанную проводником (рис. 81), имеется магнитный поток
 , (1)
, (1)
где проекция вектора  на нормаль
на нормаль  к площадке
к площадке  равна
равна  , так как вектор
, так как вектор 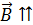
 ; площадь
; площадь 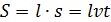 , увеличивается с течением времени
, увеличивается с течением времени 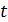 движения стержня и соответственно, согласно формуле (1), увеличивается магнитный поток
движения стержня и соответственно, согласно формуле (1), увеличивается магнитный поток 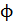 . Поэтому в стержне возникает ЭДС индукции, равная скорости изменения магнитного потока:
. Поэтому в стержне возникает ЭДС индукции, равная скорости изменения магнитного потока:
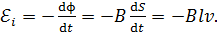 (2)
(2)
Модуль этой ЭДС 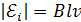 , а в замкнутой цепи сопротивлением
, а в замкнутой цепи сопротивлением 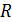 протекает индукционный ток, величина которого, согласно закону Ома:
протекает индукционный ток, величина которого, согласно закону Ома:
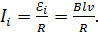 (3)
(3)
Направление индукционного тока  определим по правилу Ленца. Поскольку причина появления тока
определим по правилу Ленца. Поскольку причина появления тока  – движение стержня, то направление тока будет таким, чтобы препятствовать движению путем торможения стержня силой Ампера:
– движение стержня, то направление тока будет таким, чтобы препятствовать движению путем торможения стержня силой Ампера: 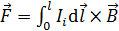 , – действующей на стержень с индукционным током. Покажем на рис. 81 тормозящую силу, как вектор
, – действующей на стержень с индукционным током. Покажем на рис. 81 тормозящую силу, как вектор 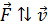 , и по правилу левой руки, размещая ладонь в плоскости рисунка, определим направление индукционного тока
, и по правилу левой руки, размещая ладонь в плоскости рисунка, определим направление индукционного тока  , соответствующее указанной силе Ампера
, соответствующее указанной силе Ампера  (см. рис. 81).
(см. рис. 81).
Мощность 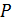 , необходимую для движения стержня с постоянной скоростью
, необходимую для движения стержня с постоянной скоростью 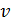 , при которой ЭДС индукции и индукционный ток, согласно формулам (2) и (3), постоянны, найдем по закону Джоуля – Ленца:
, при которой ЭДС индукции и индукционный ток, согласно формулам (2) и (3), постоянны, найдем по закону Джоуля – Ленца:
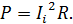 (4)
(4)
С учетом закона Ома (3) получаем расчетную формулу мощности:
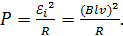 (5)
(5)
Вычисляем величину мощности
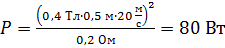 .
.
Задача 50. В проволочное кольцо, подключенное к интегратору тока (ИТ) (рис. 82), вставили прямой магнит. При этом по цепи сопротивлением 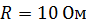 прошел заряд
прошел заряд 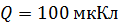 . Покажите направление индукционного тока
. Покажите направление индукционного тока  в кольце и определите магнитный поток
в кольце и определите магнитный поток 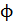 через площадь кольца.
через площадь кольца.
Дано Решение
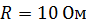 ; ;
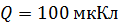 .
Направление .
Направление 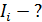
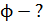
|
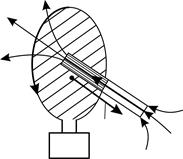
Рис. 82 |
При внесении магнита линии магнитной индукции  , создаваемой магнитом, пересекают площадь, ограниченную кольцом, и создают магнитный поток
, создаваемой магнитом, пересекают площадь, ограниченную кольцом, и создают магнитный поток 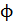 через эту площадь. Увеличение магнитного потока от начального значения
через эту площадь. Увеличение магнитного потока от начального значения 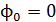 до величины
до величины 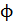 приводит к появлению ЭДС индукции
приводит к появлению ЭДС индукции 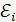 в кольце, которая определяется законом Фарадея:
в кольце, которая определяется законом Фарадея:
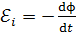 . (1)
. (1)
В замкнутой цепи сопротивлением 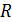 протекает индукционный ток
протекает индукционный ток  , величина которого, в соответствии с законом Ома:
, величина которого, в соответствии с законом Ома:
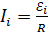 . (2)
. (2)
Протекающий в кольце индукционный ток переносит в цепи за время 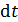 элементарный заряд
элементарный заряд 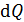 – через поперечное сечение проволоки и через интегратор тока. Сила тока, согласно определительной формуле:
– через поперечное сечение проволоки и через интегратор тока. Сила тока, согласно определительной формуле:
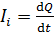 . (3)
. (3)
В интеграторе тока суммируются элементарные заряды 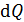 за все время протекания тока от
за все время протекания тока от 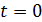 до
до 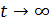 :
:
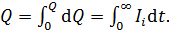 (4)
(4)
Преобразуем подинтегральное выражение (4) с учетом формул (2) и (3):
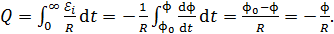 (5)
(5)
В соответствии с полученным выражением (5) записываем расчетную формулу магнитного потока через площадь кольца:
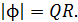
Вычисляем величину магнитного потока
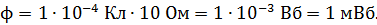
Определим направление индукционного тока  . В момент внесения магнита в кольцо увеличивается магнитный поток от нуля до некоторого значения
. В момент внесения магнита в кольцо увеличивается магнитный поток от нуля до некоторого значения 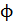 . При этом индукционный ток, согласно правилу Ленца, будет препятствовать увеличению потока
. При этом индукционный ток, согласно правилу Ленца, будет препятствовать увеличению потока 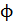 магнитным полем
магнитным полем 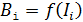 , создаваемым этим током. Чтобы уменьшать результирующее поле
, создаваемым этим током. Чтобы уменьшать результирующее поле 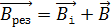 , и тем самым уменьшать магнитный поток
, и тем самым уменьшать магнитный поток 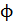 , следует быть направлению
, следует быть направлению 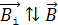 магнита. Покажем на рис. 82 направление
магнита. Покажем на рис. 82 направление 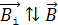 магнита, а затем, в соответствии с правилом буравчика, направим индукционный ток
магнита, а затем, в соответствии с правилом буравчика, направим индукционный ток  в кольце – против часовой стрелки.
в кольце – против часовой стрелки.
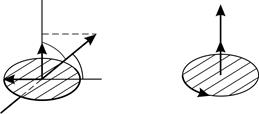
Задача 51. Кольцо массой 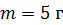 из медной проволоки расположено в однородном магнитном поле с индукцией
из медной проволоки расположено в однородном магнитном поле с индукцией 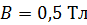 так, что плоскость кольца составляет угол
так, что плоскость кольца составляет угол 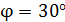 с линиями магнитной индукции. Покажите направление индукционного тока
с линиями магнитной индукции. Покажите направление индукционного тока  и определите заряд
и определите заряд 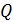 , который пройдет по кольцу, если снять магнитное поле.
, который пройдет по кольцу, если снять магнитное поле.
Дано Решение
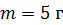 ; ;
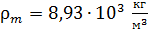 ; ;
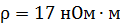 ; ;
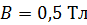 ; ;
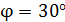 .
Направление .
Направление 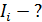
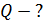
|
а б Рис. 83 |
Линии магнитной индукции однородного магнитного поля, пронизывая площадь круга 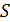 , ограниченную кольцом, создают магнитный поток
, ограниченную кольцом, создают магнитный поток 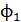 , определяемый формулой:
, определяемый формулой:
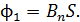 (1)
(1)
Здесь 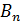 – проекция вектора
– проекция вектора  на нормаль
на нормаль 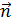 к площадке
к площадке 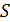 ; величина
; величина 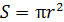 , где
, где 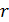 – радиус кольца. Проекция вектора
– радиус кольца. Проекция вектора  , согласно рис. 83 а:
, согласно рис. 83 а:
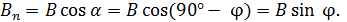 (2)
(2)
С учетом этого магнитный поток, определяемый формулой (1) запишется в виде:
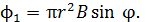 (3)
(3)
Если снять магнитное поле, например, отключив ток в обмотке электромагнита, то магнитный поток уменьшится до нуля: 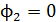 . При уменьшении магнитного потока в кольце индуцируется ЭДС
. При уменьшении магнитного потока в кольце индуцируется ЭДС 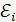 , величина которой, согласно закону Фарадея:
, величина которой, согласно закону Фарадея:
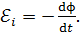 (4)
(4)
В замкнутом кольце потечет индукционный ток  , величина которого определяется законом Ома:
, величина которого определяется законом Ома:
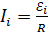 , (5)
, (5)
где 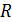 – сопротивление проволочного кольца длиной
– сопротивление проволочного кольца длиной 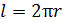 и площадью сечения проволоки
и площадью сечения проволоки 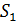 . Величина сопротивления определяется формулой
. Величина сопротивления определяется формулой
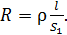 (6)
(6)
При протекании индукционного тока по кольцу переносится заряд величиной 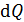 за время
за время 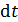 :
:
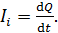 (7)
(7)
Весь заряд 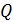 , который пройдет по кольцу, найдем, суммируя элементарные заряды
, который пройдет по кольцу, найдем, суммируя элементарные заряды 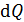 за все время протекания тока:
за все время протекания тока:
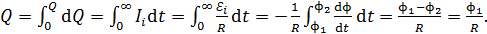 (8)
(8)
С учетом формул (3) и (6) формула (8) для определения заряда принимает следующий вид:
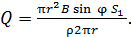 (9)
(9)
Размеры кольца – длина 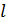 , радиус
, радиус 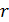 , а также площадь сечения проволоки
, а также площадь сечения проволоки 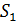 связаны с массой кольца
связаны с массой кольца 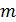 , его объемом
, его объемом 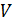 и плотностью меди
и плотностью меди 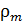 следующими соотношениями:
следующими соотношениями:
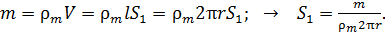
Подставляя величину 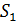 в формулу (9), получаем следующую расчетную формулу искомой величины заряда:
в формулу (9), получаем следующую расчетную формулу искомой величины заряда:
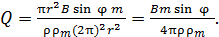 (10)
(10)
Проверим полученную формулу по единицам величин, в нее входящих:
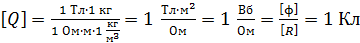 .
.
Вычислим по формуле (10) заряд, прошедший по кольцу при снятии магнитного поля:
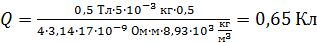 .
.
Определим направление индукционного тока по правилу Ленца. При уменьшении величины магнитной индукции  и проекции вектора
и проекции вектора 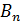 индукционный ток
индукционный ток  будет препятствовать этому уменьшению, создавая магнитное поле с индукцией
будет препятствовать этому уменьшению, создавая магнитное поле с индукцией 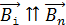 (рис. 83 б), чтобы сохранить прежний магнитный поток. Покажем на рисунке вектор
(рис. 83 б), чтобы сохранить прежний магнитный поток. Покажем на рисунке вектор 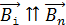 и по правилу буравчика определим направление индукционного тока в кольце: он течет против часовой стрелки, если смотреть на кольцо сверху.
и по правилу буравчика определим направление индукционного тока в кольце: он течет против часовой стрелки, если смотреть на кольцо сверху.
Задача 52. Соленоид, имеющий сердечник площадью сечения 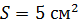 и обмотку, содержащую
и обмотку, содержащую 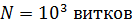 , при токе
, при токе 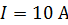 создает внутри сердечника магнитное поле с индукцией
создает внутри сердечника магнитное поле с индукцией 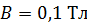 . Определите индуктивность
. Определите индуктивность 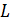 соленоида и энергию
соленоида и энергию 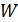 его магнитного поля.
его магнитного поля.
Дано Решение
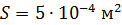 ; ;
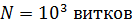 ; ;
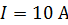 ; ;
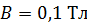 . .
|
Индуктивность соленоида 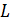 характеризует его способность создавать собственный магнитный поток
характеризует его способность создавать собственный магнитный поток 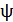 . Индуктивность
. Индуктивность 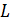 является коэффициентом пропорциональности между потокосцеплением
является коэффициентом пропорциональности между потокосцеплением 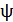 соленоида и током
соленоида и током 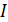 в его обмотке:
в его обмотке:
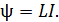 (1)
(1)
Формулу (1) используем для расчета индуктивности; с этой целью определим потокосцепление соленоида:
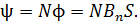 (2)
(2)
Здесь 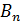 – проекция вектора
– проекция вектора  на нормаль
на нормаль 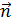 к сечению
к сечению 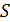 , ее величина
, ее величина  . Определяем индуктивность соленоида
. Определяем индуктивность соленоида 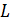 из формулы (1) с учетом формулы (2) для потокосцепления
из формулы (1) с учетом формулы (2) для потокосцепления 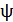 :
:
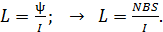 (3)
(3)
Вычисляем индуктивность заданного соленоида:
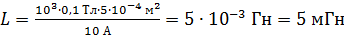 .
.
Энергию магнитного поля соленоида с током 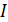 в его обмотке определяем по следующей формуле:
в его обмотке определяем по следующей формуле:
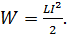 (4)
(4)
Вычисляем величину энергии магнитного поля соленоида:
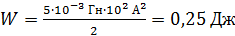 .
.
Задача 53. Электрическая цепь, схема которой приведена на рис. 84, содержит катушку индуктивностью 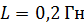 и сопротивлением
и сопротивлением 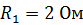 и резистор сопротивлением
и резистор сопротивлением 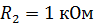 . В цепи течет ток
. В цепи течет ток 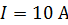 . Определите силу тока
. Определите силу тока 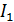 в катушке и
в катушке и 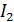 – в резисторе в трех случаях: 1) до размыкания цепи, 2) в момент размыкания (
– в резисторе в трех случаях: 1) до размыкания цепи, 2) в момент размыкания ( 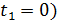 , 3) через
, 3) через 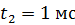 после размыкания. Покажите направление индукционного тока в цепи после размыкания. Сопротивлением источника тока можно пренебречь.
после размыкания. Покажите направление индукционного тока в цепи после размыкания. Сопротивлением источника тока можно пренебречь.
Дано Решение
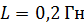 ; ;
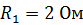 ; ;
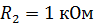 ; ;
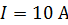 . .
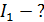 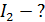 В трех случаях:
1) ключ К замкнут; В трех случаях:
1) ключ К замкнут;
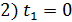 ; 3) ; 3) 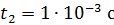 .
Направление .
Направление 
|
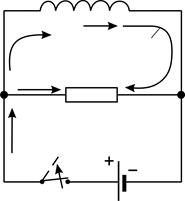
Рис. 84 |
Катушка и параллельно соединенный с ней резистор подключены к источнику тока. Потребляемый от источника ток в узле  (см. рис. 84) разветвляется на два, удовлетворяющих первому правилу Кирхгофа:
(см. рис. 84) разветвляется на два, удовлетворяющих первому правилу Кирхгофа:
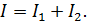 (1)
(1)
Чтобы найти токи 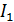 и
и 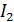 , запишем второе правило Кирхгофа для двух контуров, содержащих а) катушку и источник тока:
, запишем второе правило Кирхгофа для двух контуров, содержащих а) катушку и источник тока: 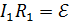 , б) резистор и источник тока:
, б) резистор и источник тока: 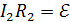 . Приравнивая последние уравнения, находим соотношение токов:
. Приравнивая последние уравнения, находим соотношение токов:
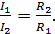 (2)
(2)
Решая совместно уравнения (1) и (2), определяем токи 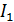 и
и 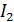 до размыкания цепи ключом
до размыкания цепи ключом 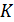 :
:
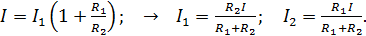 (3)
(3)
Вычисляем силу тока в ветвях до размыкания цепи:
а) через резистор: 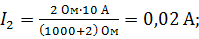
б) через катушку: 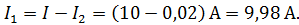
2) После отключения источника тока размыканием ключа 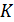 в замкнутом контуре, содержащем катушку индуктивностью
в замкнутом контуре, содержащем катушку индуктивностью 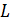 и резистор, ток снижается. Следовательно, в катушке возникает ЭДС самоиндукции
и резистор, ток снижается. Следовательно, в катушке возникает ЭДС самоиндукции 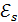 , которая в случае постоянной индуктивности
, которая в случае постоянной индуктивности 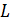 определяется формулой:
определяется формулой:
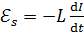 . (4)
. (4)
Ток в контуре, создаваемый этой ЭДС, определяется законом Ома:
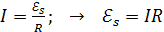 . (5)
. (5)
Здесь 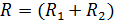 – сопротивление контура, в котором катушка и резистор соединены последовательно. Величина
– сопротивление контура, в котором катушка и резистор соединены последовательно. Величина 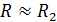 , так как первым слагаемым в формуле можно пренебречь из-за его малости:
, так как первым слагаемым в формуле можно пренебречь из-за его малости: 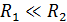 .
.
Ток в контуре 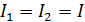 – это индукционный ток
– это индукционный ток  . Его направление определяем по правилу Ленца: так как ток
. Его направление определяем по правилу Ленца: так как ток 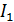 в катушке снижается (что приводит к снижению магнитного потока), то индукционный ток, препятствуя этому снижению, будет направлен так же, как и снижающийся ток
в катушке снижается (что приводит к снижению магнитного потока), то индукционный ток, препятствуя этому снижению, будет направлен так же, как и снижающийся ток 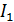 (см. рис. 84). При этом ток через резистор изменит направление на противоположное тому, которое было с подключенным источником тока.
(см. рис. 84). При этом ток через резистор изменит направление на противоположное тому, которое было с подключенным источником тока.
Найдем силу индукционного тока 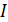 , как функцию времени
, как функцию времени 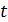 . Для этого приравняем величину ЭДС самоиндукции
. Для этого приравняем величину ЭДС самоиндукции 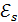 по формулам (4) и (5):
по формулам (4) и (5):
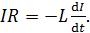 (6)
(6)
Это простое дифференциальное уравнение решаем, разделяя переменные:
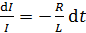 .
.
Интегрируем равенство со следующими пределами: от тока в катушке 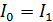 в начальный момент времени
в начальный момент времени 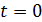 до тока
до тока 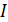 – в произвольный момент времени
– в произвольный момент времени 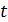 :
:
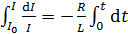 ;
; 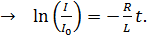
Потенцируя это уравнение, получаем закон изменения индукционного тока в цепи с течением времени 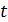 от момента отключения источника тока:
от момента отключения источника тока:
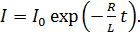 (7)
(7)
Согласно уравнению (7), в момент размыкания цепи ( 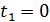 ) ток в цепи, протекающий через катушку и резистор:
) ток в цепи, протекающий через катушку и резистор:
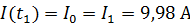 .
.
Ток в момент времени 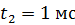 вычисляем по уравнению (7):
вычисляем по уравнению (7):
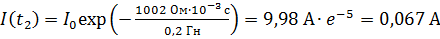 .
.
Таким образом, экстраток самоиндукции  в начальный момент времени совпадает с током в катушке, а для высокоомного сопротивления
в начальный момент времени совпадает с током в катушке, а для высокоомного сопротивления 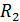 этот индукционный ток в
этот индукционный ток в 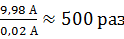 превышает «рабочий ток»
превышает «рабочий ток» 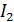 от источника тока. Даже спустя 1 мс после размыкания ключа
от источника тока. Даже спустя 1 мс после размыкания ключа  примерно в 3 раза больше, чем
примерно в 3 раза больше, чем 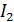 . В результате протекания индукционного тока в катушке и в резисторе выделяется тепловая энергия, равная энергии магнитного поля катушки до размыкания ключа:
. В результате протекания индукционного тока в катушке и в резисторе выделяется тепловая энергия, равная энергии магнитного поля катушки до размыкания ключа:
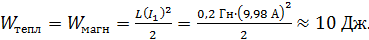
Задача 54. Катушку сопротивлением 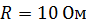 замкнули на источник тока. Через время
замкнули на источник тока. Через время 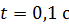 от момента замыкания сила тока в катушке достигла 0,90
от момента замыкания сила тока в катушке достигла 0,90 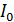 – предельного значения. Определите индуктивность катушки
– предельного значения. Определите индуктивность катушки 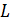 и укажите направление индукционного тока в цепи.
и укажите направление индукционного тока в цепи.
Дано Решение
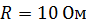 ; ;
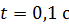 ; ;
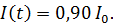
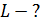 Направление
Направление 
|
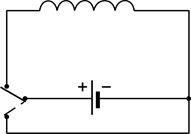
Рис. 85 |
При замыкании катушки ключом  на источник тока с ЭДС
на источник тока с ЭДС 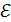 (рис. 85) ток в катушке увеличивается, создавая в ней магнитное поле, и потокосцепление катушки возрастает. В результате изменения тока в катушке возникает ЭДС самоиндукции
(рис. 85) ток в катушке увеличивается, создавая в ней магнитное поле, и потокосцепление катушки возрастает. В результате изменения тока в катушке возникает ЭДС самоиндукции 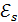 , которая изменяется с течением времени, согласно закону электромагнитной индукции:
, которая изменяется с течением времени, согласно закону электромагнитной индукции:
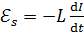 . (1)
. (1)
ЭДС самоиндукции создает в цепи индукционный ток  , направление которого определим по правилу Ленца. Этот индукционный ток будет препятствовать нарастанию тока в цепи (и потокосцепления катушки), следовательно, он направлен противоположно току
, направление которого определим по правилу Ленца. Этот индукционный ток будет препятствовать нарастанию тока в цепи (и потокосцепления катушки), следовательно, он направлен противоположно току 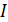 от источника тока. Вследствие этого, ток в цепи, в соответствии с законом Ома:
от источника тока. Вследствие этого, ток в цепи, в соответствии с законом Ома:
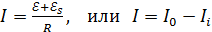 , (2)
, (2)
где 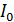 – установившееся значение тока в цепи: когда индукционный ток
– установившееся значение тока в цепи: когда индукционный ток  снизится до нуля, его величина
снизится до нуля, его величина
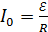 . (3)
. (3)
Зависимость индукционного тока от времени можно найти, как и в решении предыдущей задачи, рассматривая отключение источника тока без размыкания цепи путем перевода ключа  из положения 1 в 2 (см. рис. 85). При этом в цепи протекает только индукционный ток
из положения 1 в 2 (см. рис. 85). При этом в цепи протекает только индукционный ток  и в соответствии с законом Ома (2):
и в соответствии с законом Ома (2):
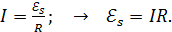 (4)
(4)
Приравнивая значения ЭДС самоиндукции 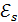 по уравнениям (1) и (4), получаем дифференциальное уравнение
по уравнениям (1) и (4), получаем дифференциальное уравнение
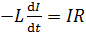 .
.
Разделяя переменные, преобразуем это уравнение к виду:
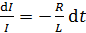 .
.
Интегрируя: 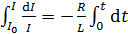 , получаем зависимость индукционного тока от времени в следующем виде:
, получаем зависимость индукционного тока от времени в следующем виде:
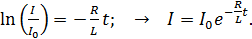 (5)
(5)
Найденное значение индукционного тока (в уравнении (5) 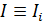 ) в виде
) в виде 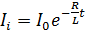 подставим в закон Ома (2) и получим закон установления тока в катушке при подключении ее к источнику тока:
подставим в закон Ома (2) и получим закон установления тока в катушке при подключении ее к источнику тока:
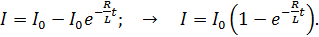 (6)
(6)
Из этого уравнения видим, что 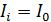 при
при 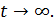
Чтобы определить индуктивность катушки 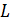 , преобразуем уравнение (6) следующим образом:
, преобразуем уравнение (6) следующим образом:
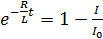 .
.
Логарифмируя последнее равенство, получаем расчетную формулу для определения индуктивности катушки:
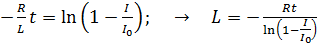 . (7)
. (7)
Вычисляем величину индуктивности катушки:
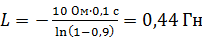 .
.
Заметим, что в решении данной задачи можно было найти зависимость тока от времени 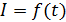 в виде уравнения (6) путем составления дифференциального уравнения из уравнений (1) и (2), но в этом случае решение полученного дифференциального уравнения оказалось бы более сложным. Заметим также, что рассмотренный в задаче метод определения индуктивности катушки приемлем для измерения величин
в виде уравнения (6) путем составления дифференциального уравнения из уравнений (1) и (2), но в этом случае решение полученного дифференциального уравнения оказалось бы более сложным. Заметим также, что рассмотренный в задаче метод определения индуктивности катушки приемлем для измерения величин 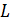 контуров с большой индуктивностью – порядка 1 Гн и более.
контуров с большой индуктивностью – порядка 1 Гн и более.
Магнитное поле в веществе
План решения задач
1. При расчете магнитного поля катушки с ферромагнитным сердечником следует иметь в виду, что индукция магнитного поля  в таком сердечнике зависит от напряженности МП
в таком сердечнике зависит от напряженности МП 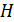 . Причем, вид зависимости
. Причем, вид зависимости 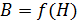 для конкретного материала сердечника устанавливается экспериментально. Как правило, в справочной литературе и в задачниках по физике приводят графики зависимостей
для конкретного материала сердечника устанавливается экспериментально. Как правило, в справочной литературе и в задачниках по физике приводят графики зависимостей 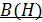 .
.
2. Чтобы воспользоваться такой зависимостью, вычисляют напряженность магнитного поля 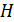 , обычно, с помощью теоремы о циркуляции вектора
, обычно, с помощью теоремы о циркуляции вектора 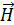 . В правой части теоремы записывают сумму токов, охватываемых контуром интегрирования
. В правой части теоремы записывают сумму токов, охватываемых контуром интегрирования 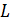 (вдоль которого определяется циркуляция), как число ампер-витков катушки
(вдоль которого определяется циркуляция), как число ампер-витков катушки 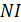 . Это произведение числа витков
. Это произведение числа витков 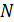 в обмотке катушки на силу тока
в обмотке катушки на силу тока 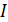 .
.
3. Магнитную проницаемость 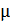 материала сердечника вычисляют по формуле связи величин
материала сердечника вычисляют по формуле связи величин 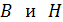 :
: 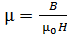 . Отметим, что величина магнитной проницаемости
. Отметим, что величина магнитной проницаемости 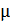 зависит не только от напряженности намагничивающего поля, но и от размеров и формы ферромагнитного сердечника. Для бесконечного (тороидального или кольцевого) сердечника величина
зависит не только от напряженности намагничивающего поля, но и от размеров и формы ферромагнитного сердечника. Для бесконечного (тороидального или кольцевого) сердечника величина 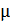 наибольшая и достигает значений
наибольшая и достигает значений 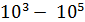 . Поперечная прорезь в сердечнике приводит к существенному снижению его магнитной проницаемости.
. Поперечная прорезь в сердечнике приводит к существенному снижению его магнитной проницаемости.
Задача 55. Магнитный момент атома железа 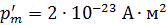 . Оцените магнитный момент
. Оцените магнитный момент 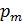 железного бруска длиной
железного бруска длиной 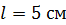 и площадью сечения
и площадью сечения 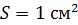 , намагниченного до насыщения. Определите максимальный вращающий момент
, намагниченного до насыщения. Определите максимальный вращающий момент 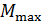 , который действовал бы на такой железный брусок в магнитном поле с индукцией
, который действовал бы на такой железный брусок в магнитном поле с индукцией 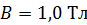 .
.
Дано Решение
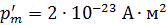 ; ;
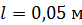 ; ;
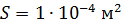 ; ;
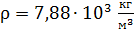 ; ;
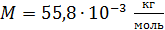 ; ;
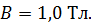
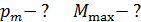
|
Железный брусок, как и другие ферромагнетики, состоит из доменов. Домен – это область самопроизвольной намагниченности вещества, причем, в пределах домена векторы магнитных моментов всех атомов сонаправлены, т. е. каждый домен намагничен до насыщения. Размер домена порядка (0,01…0,1) мм, число атомов вещества в таком домене 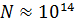 . В размагниченном состоянии ферромагнетика магнитные моменты его доменов
. В размагниченном состоянии ферромагнетика магнитные моменты его доменов 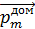 имеют хаотическую ориентацию. Но во внешнем магнитном поле с индукцией
имеют хаотическую ориентацию. Но во внешнем магнитном поле с индукцией  на каждый домен, имеющий магнитный момент
на каждый домен, имеющий магнитный момент 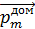 , действует механический (вращающий) момент
, действует механический (вращающий) момент 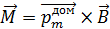 , модуль которого
, модуль которого 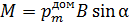 . В результате поворота магнитных моментов доменов сначала растут домены, у которых угол
. В результате поворота магнитных моментов доменов сначала растут домены, у которых угол 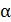 между векторами
между векторами 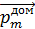
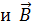 мал. На заключительной стадии намагничивания ферромагнетика происходит поворот магнитных моментов выросших доменов до состояния с
мал. На заключительной стадии намагничивания ферромагнетика происходит поворот магнитных моментов выросших доменов до состояния с 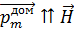 , где
, где 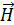 – напряженность намагничивающего поля. При этом образец представляет собой один домен, магнитный момент которого
– напряженность намагничивающего поля. При этом образец представляет собой один домен, магнитный момент которого
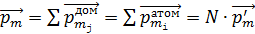 , (1)
, (1)
где 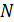 – число атомов в бруске;
– число атомов в бруске; 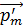 – магнитный момент атома железа.
– магнитный момент атома железа.
Таким образом, в бруске ферромагнетика, намагниченном до насыщения, магнитные моменты всех атомов сонаправлены. В результате этого, согласно равенству (1), модуль магнитного момента железного бруска определяется следующей формулой:
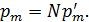 (2)
(2)
Число атомов 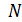 в бруске определим, используя число Авогадро
в бруске определим, используя число Авогадро 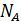 , равное числу атомов в одном моле вещества, умножая это число на количество вещества (число молей)
, равное числу атомов в одном моле вещества, умножая это число на количество вещества (число молей) 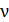 :
:
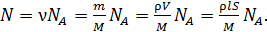 (3)
(3)
Здесь 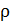 – плотность железа;
– плотность железа; 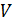 – объем бруска, имеющего размеры
– объем бруска, имеющего размеры 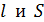 ;
; 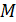 – молярная масса железа.
– молярная масса железа.
Подставляя число атомов 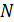 по формуле (3) в равенство (2), получаем расчетную формулу магнитного момента бруска в виде:
по формуле (3) в равенство (2), получаем расчетную формулу магнитного момента бруска в виде:
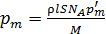 .
.
Вычислим магнитный момент данного железного бруска, намагниченного до насыщения:
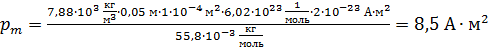 .
.
Полученная величина магнитного момента бруска является достаточно большой. Такой магнитный момент имел бы виток: 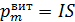 , например, при токе
, например, при токе 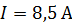 и площади витка
и площади витка 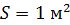 . Другой объект, имеющий магнитный момент, – соленоид; для него величина
. Другой объект, имеющий магнитный момент, – соленоид; для него величина 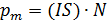 , где
, где 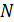 – число витков. Вычислим магнитный момент соленоида, имеющего ту же площадь сечения, как и брусок:
– число витков. Вычислим магнитный момент соленоида, имеющего ту же площадь сечения, как и брусок: 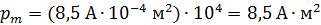 . Этот оценочный расчет показывает, что катушка с воздушным сердечником имеет такой же магнитный момент, как и железный брусок, при числе витков катушки
. Этот оценочный расчет показывает, что катушка с воздушным сердечником имеет такой же магнитный момент, как и железный брусок, при числе витков катушки 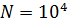 .
.
Механический момент 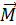 , действующий в магнитном поле с индукцией
, действующий в магнитном поле с индукцией  на объект, обладающий магнитным моментом
на объект, обладающий магнитным моментом 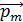 , определяется следующей формулой:
, определяется следующей формулой:
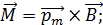 модуль
модуль 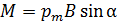 , (4)
, (4)
где 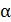 – угол между векторами
– угол между векторами 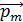 и
и  .
.
Максимальная величина механического момента 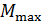 , согласно формуле (4), наблюдается при значении
, согласно формуле (4), наблюдается при значении 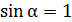 , т. е. при расположении вектора магнитного момента бруска
, т. е. при расположении вектора магнитного момента бруска 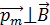 . Вычисляем эту величину по формуле (4):
. Вычисляем эту величину по формуле (4):
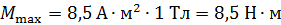 .
.
Для того чтобы удержать такой намагниченный железный брусок в положении, при котором его магнитный момент 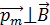 , необходимо к концам бруска приложить пару сил, каждая из которых
, необходимо к концам бруска приложить пару сил, каждая из которых 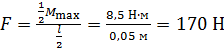 . Это сила тяжести
. Это сила тяжести 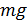 груза массой 17 кг. Такой оценочный расчет показывает, как велики магнитные силы, действующие на ферромагнитные объекты.
груза массой 17 кг. Такой оценочный расчет показывает, как велики магнитные силы, действующие на ферромагнитные объекты.
Задача 56. Железное кольцо средним радиусом 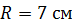 и площадью поперечного сечения
и площадью поперечного сечения 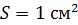 является сердечником кольцевого соленоида. Его обмотка содержит
является сердечником кольцевого соленоида. Его обмотка содержит 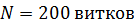 с током
с током 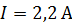 . Определите магнитную индукцию
. Определите магнитную индукцию  поля в сердечнике, магнитный поток
поля в сердечнике, магнитный поток 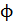 в сечении кольца и магнитную проницаемость сердечника
в сечении кольца и магнитную проницаемость сердечника 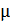 . Используйте график основной кривой намагничивания железа:
. Используйте график основной кривой намагничивания железа: 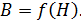
|
Железное кольцо:
 ; ;
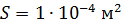 ; ;
|
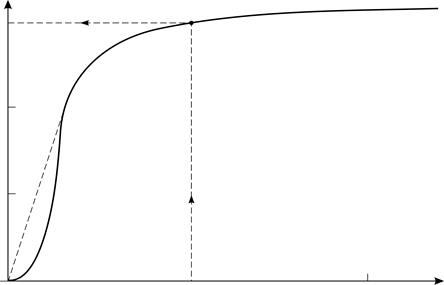
Рис. 86 |
|
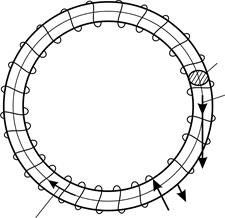
Рис. 87 |
Так как магнитная индукция  железного сердечника зависит от напряженности
железного сердечника зависит от напряженности 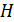 магнитного поля в нем (рис. 86), рассчитаем величину
магнитного поля в нем (рис. 86), рассчитаем величину 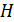 при заданном токе. Для этого запишем теорему о циркуляции вектора
при заданном токе. Для этого запишем теорему о циркуляции вектора 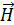 вдоль контура интегрирования
вдоль контура интегрирования 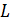 , совпадающего со средней линией кольца, длина которой
, совпадающего со средней линией кольца, длина которой 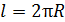 . Направление обхода по контуру
. Направление обхода по контуру 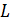 (рис. 87) выбираем так, чтобы проекция
(рис. 87) выбираем так, чтобы проекция 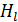 вектора
вектора 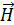 на направление элемента длины контура
на направление элемента длины контура 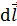 была положительной. В таком случае
была положительной. В таком случае
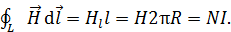 (1)
(1)
Из этого уравнения определяем напряженность МП и вычисляем ее:
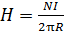 .
. 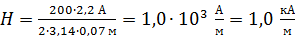 .
.
По графику 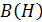 (см. рис. 86) для найденной величины
(см. рис. 86) для найденной величины 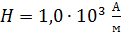 определяем
определяем 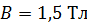 .
.
Магнитный поток в сечении сердечника определяем с учетом того, что линии магнитной индукции (сонаправленные линиям напряженности МП) являются окружностями, концентрическими кольцу. Такие линии поля перпендикулярны сечению сердечника площадью 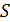 (см. рис. 87), поэтому проекция вектора
(см. рис. 87), поэтому проекция вектора  на нормаль к сечению
на нормаль к сечению  . Магнитное поле в тонком кольце практически однородно и магнитный поток
. Магнитное поле в тонком кольце практически однородно и магнитный поток 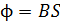 .
.
Вычисляем магнитный поток в сечении железного сердечника:
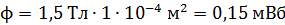 .
.
Величина магнитной проницаемости железного сердечника
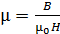 .
.
Вычисляем по этой формуле магнитную проницаемость железа при найденной напряженности МП и соответствующем ей значении  :
:
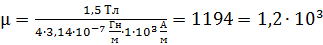 .
.
Это значение не является максимальным для железа. С помощью графика 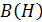 можно оценить наибольшее значение магнитной проницаемости
можно оценить наибольшее значение магнитной проницаемости 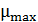 по наибольшему угловому коэффициенту
по наибольшему угловому коэффициенту 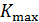 прямой
прямой 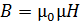 :
:
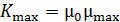 . По графику находим величину
. По графику находим величину 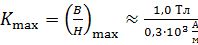 . Соответствующее значение
. Соответствующее значение 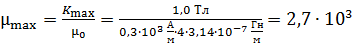 .
.
Задача 57. Тороидальная катушка с железным сердечником, длина осевой линии которого 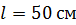 , имеет обмотку, содержащую
, имеет обмотку, содержащую 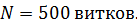 При токе в обмотке тороида
При токе в обмотке тороида 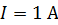 индукция магнитного поля в сердечнике
индукция магнитного поля в сердечнике 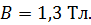 Какой ток
Какой ток 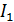 нужно пропустить по обмотке для получения магнитного поля с такой же величиной
нужно пропустить по обмотке для получения магнитного поля с такой же величиной  в воздушном зазоре сердечника? Длина воздушного промежутка
в воздушном зазоре сердечника? Длина воздушного промежутка 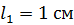 (рис. 88), рассеянием магнитного потока в зазоре можно пренебречь.
(рис. 88), рассеянием магнитного потока в зазоре можно пренебречь.
Дано Решение
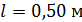 ; ;
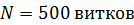 ; ;
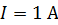 ; ;
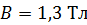 ; ;
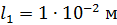 . .
|
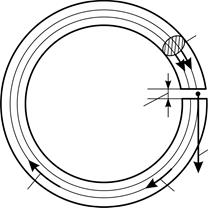
Рис. 88 |
Если пренебречь рассеянием магнитного потока в зазоре, т. е. принять, что магнитный поток в сердечнике 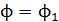 – магнитному потоку в воздушном промежутке, то
– магнитному потоку в воздушном промежутке, то
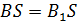 ;
; 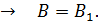
Таким образом, магнитная индукция поля в сердечнике и в воздушном промежутке одинакова. Но напряженности МП различны:
а) в сердечнике с магнитной проницаемостью 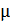 величина
величина 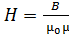 ; (1)
; (1)
б) в воздушном промежутке (для воздуха 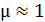 ) –
) – 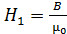 . (2)
. (2)
Величина магнитной индукции 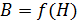 ; эта зависимость для железа задана графиком (см. рис. 86). Для получения той же величины
; эта зависимость для железа задана графиком (см. рис. 86). Для получения той же величины 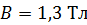 в случае сердечника с зазором напряженность магнитного поля
в случае сердечника с зазором напряженность магнитного поля 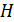 внутри сердечника должна быть такой же, как и в сплошном сердечнике (это одна и та же точка на графике
внутри сердечника должна быть такой же, как и в сплошном сердечнике (это одна и та же точка на графике 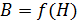 ).
).
С учетом этих замечаний запишем теорему о циркуляции вектора 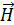 вдоль контура интегрирования
вдоль контура интегрирования 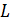 , совпадающего с осевой линией сердечника. Искомый ток
, совпадающего с осевой линией сердечника. Искомый ток 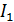 содержится в правой части теоремы:
содержится в правой части теоремы:
а) для сплошного сердечника –
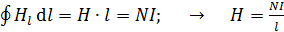 ; (3)
; (3)
б) в случае сердечника с воздушным промежутком (см. рис. 88) –
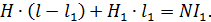 (4)
(4)
Подставляя значения напряженностей МП, определяемые формулами (2) и (3), в уравнение (4), получаем следующее равенство:
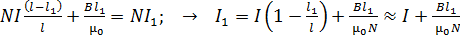 . (5)
. (5)
Здесь учтено, что длина зазора 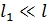 , следовательно,
, следовательно, 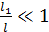 .
.
Вычисляем ток в обмотке по формуле (5):
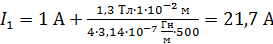 .
.
Таким образом, для намагничивания железного сердечника с воздушным промежутком требуется существенно больший ток, чем в случае сплошного сердечника.
Задача 58. Для сердечника тороида с прорезью, описанного в предыдущей задаче, определите магнитную проницаемость 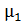 . Сравните величину
. Сравните величину 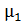 с магнитной проницаемостью
с магнитной проницаемостью 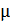 сплошного сердечника того же тороида.
сплошного сердечника того же тороида.
Дано Решение
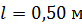 ; ;
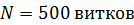 ; ;
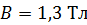 ; ;
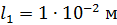 . .
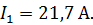
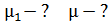
|
В случае сердечника с прорезью запишем теорему о циркуляции вектора 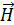 (см. уравнение (4) в решении предыдущей задачи):
(см. уравнение (4) в решении предыдущей задачи):
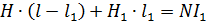 . (1)
. (1)
В это уравнение подставим значения напряженностей магнитного поля в сердечнике: 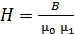 , и в воздушном промежутке –
, и в воздушном промежутке – 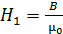 . При этом уравнение (1) принимает следующий вид:
. При этом уравнение (1) принимает следующий вид:
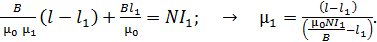 (2)
(2)
Заметим, что полученное выражение (2) является только расчетной формулой величины 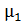 и не передает зависимость
и не передает зависимость 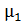 от длины зазора. Вычисляем магнитную проницаемость железного сердечника с воздушным промежутком по формуле (2):
от длины зазора. Вычисляем магнитную проницаемость железного сердечника с воздушным промежутком по формуле (2):
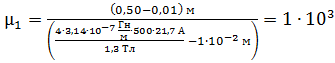 .
.
Для сплошного железного сердечника из формулы связи величин 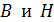 :
: 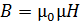 , – определяем магнитную проницаемость сердечника:
, – определяем магнитную проницаемость сердечника:
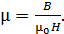 (3)
(3)
Необходимое значение напряженности 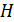 поля, намагничивающего сердечник до величины магнитной индукции
поля, намагничивающего сердечник до величины магнитной индукции 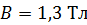 , определяем по графику
, определяем по графику 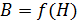 (см. рис. 86):
(см. рис. 86): 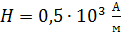 . Используя эти значения
. Используя эти значения 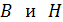 , вычисляем магнитную проницаемость сплошного железного сердечника по формуле (3):
, вычисляем магнитную проницаемость сплошного железного сердечника по формуле (3):
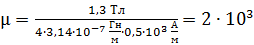 .
.
Таким образом, прорезь длиной 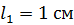 в железном сердечнике вдвое понижает его магнитную проницаемость.
в железном сердечнике вдвое понижает его магнитную проницаемость.
Задача 59. Тонкий кольцевой ферромагнитный сердечник средним радиусом 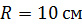 имеет поперечную прорезь длиной
имеет поперечную прорезь длиной 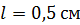 . Сердечник был намагничен током, протекающим по обмотке, после чего ток отключили. Определите, во сколько раз напряженность магнитного поля
. Сердечник был намагничен током, протекающим по обмотке, после чего ток отключили. Определите, во сколько раз напряженность магнитного поля 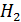 в воздушном зазоре превышает напряженность
в воздушном зазоре превышает напряженность 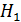 МП в сердечнике. Оцените магнитную проницаемость
МП в сердечнике. Оцените магнитную проницаемость 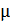 ферромагнитного сердечника.
ферромагнитного сердечника.
Дано Решение
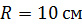 ; ;
 . .

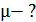
|

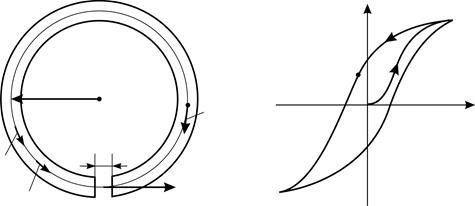
Рис. 89 Рис. 90 |
Запишем теорему о циркуляции вектора 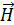 вдоль контура
вдоль контура 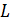 , совпадающего со средней линией сердечника (рис. 89). Направление обхода по контуру интегрирования выберем вдоль вектора магнитной индукции
, совпадающего со средней линией сердечника (рис. 89). Направление обхода по контуру интегрирования выберем вдоль вектора магнитной индукции 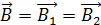 (рассеянием магнитного потока в воздушном зазоре пренебрегаем). Так как ток в обмотке отсутствует:
(рассеянием магнитного потока в воздушном зазоре пренебрегаем). Так как ток в обмотке отсутствует: 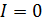 , – то теорема запишется в следующем виде:
, – то теорема запишется в следующем виде:
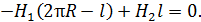 (1)
(1)
Здесь проекция вектора напряженности 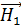 в сердечнике
в сердечнике 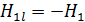 , так как после отключения намагничивающего поля напряженностью
, так как после отключения намагничивающего поля напряженностью 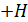 соотношение величин
соотношение величин 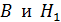 в магнитном поле сердечника соответствует точке
в магнитном поле сердечника соответствует точке 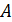 на верхней ветви петли гистерезиса (рис. 90). Из уравнения (1) находим искомое отношение напряженностей:
на верхней ветви петли гистерезиса (рис. 90). Из уравнения (1) находим искомое отношение напряженностей:
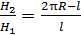 .
.
Вычисляем это отношение, показывающее, во сколько раз напряженность магнитного поля 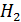 в воздушном зазоре превышает напряженность
в воздушном зазоре превышает напряженность 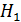 МП в сердечнике:
МП в сердечнике:
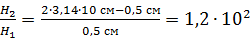 .
.
Для определения магнитной проницаемости 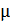 ферромагнитного сердечника используем формулы связи магнитной индукции
ферромагнитного сердечника используем формулы связи магнитной индукции  с напряженностью магнитного поля
с напряженностью магнитного поля 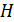 :
:
а) в сердечнике величина 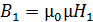 ;
;
б) в зазоре – 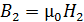 , так как для воздуха
, так как для воздуха 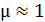 .
.
Приравнивая 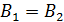 , в силу непрерывности линий магнитной индукции, получаем расчетную формулу магнитной проницаемости сердечника после отключения тока в намагничивающей обмотке:
, в силу непрерывности линий магнитной индукции, получаем расчетную формулу магнитной проницаемости сердечника после отключения тока в намагничивающей обмотке:
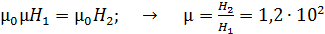 .
.
Задача 60. Тороидальная катушка с железным сердечником, длина осевой линии которого 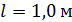 , имеет обмотку, содержащую
, имеет обмотку, содержащую 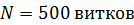 с током
с током 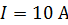 . В сердечнике имеется поперечная прорезь длиной
. В сердечнике имеется поперечная прорезь длиной 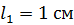 (рис. 91). Определите индукцию магнитного поля
(рис. 91). Определите индукцию магнитного поля  в сердечнике и в зазоре. Рассеянием магнитного потока в зазоре можно пренебречь.
в сердечнике и в зазоре. Рассеянием магнитного потока в зазоре можно пренебречь.
Дано Решение
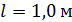 ; ;
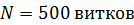 ; ;
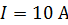 ; ;
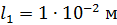 . .
|
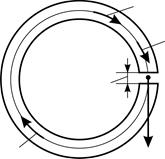
Рис. 91 |
Для материала сердечника – железа, величина магнитной индукции  зависит от напряженности магнитного поля
зависит от напряженности магнитного поля 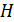 в соответствии с экспериментальной кривой намагничивания
в соответствии с экспериментальной кривой намагничивания 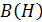 (см. рис. 86). Величина напряженности магнитного поля
(см. рис. 86). Величина напряженности магнитного поля 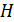 зависит от тока в обмотке катушки. Запишем теорему о циркуляции вектора
зависит от тока в обмотке катушки. Запишем теорему о циркуляции вектора 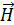 вдоль контура интегрирования
вдоль контура интегрирования 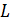 , совпадающего с осевой линией тороидального сердечника (см. рис. 91):
, совпадающего с осевой линией тороидального сердечника (см. рис. 91):
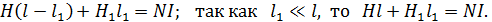 (1)
(1)
Здесь напряженность МП в воздушном зазоре 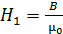 , так как для воздуха
, так как для воздуха 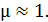 С учетом этого теорему (1) запишем в следующем виде:
С учетом этого теорему (1) запишем в следующем виде:
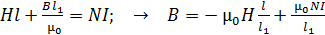 . (2)
. (2)
Получено уравнение прямой линии 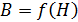 для заданного в задаче тороидального сердечника с воздушным промежутком.
для заданного в задаче тороидального сердечника с воздушным промежутком.
Итак, имеется две зависимости, связывающие переменные 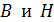 : 1) график кривой намагничивания железа
: 1) график кривой намагничивания железа 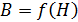 и 2) зависимость
и 2) зависимость 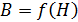 , описываемая уравнением (2). Имея две зависимости, можем определить две неизвестные величины –
, описываемая уравнением (2). Имея две зависимости, можем определить две неизвестные величины – 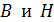 . Так как одна из зависимостей экспериментальная, и задана графиком, то решим систему двух уравнений
. Так как одна из зависимостей экспериментальная, и задана графиком, то решим систему двух уравнений 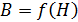 графическим методом. Для этого построим линейную зависимость (2) на поле кривой намагничивания (рис. 92).
графическим методом. Для этого построим линейную зависимость (2) на поле кривой намагничивания (рис. 92).
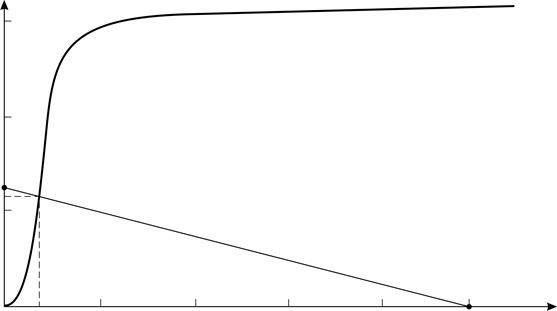
Рис. 92 |
Для проведения прямой линии достаточно знать две точки; их координаты определим по уравнению (2), выбрав удобные для вычислений точки: одна из них – точка 1, координаты которой равны 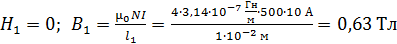 ; вторая – точка 2:
; вторая – точка 2: 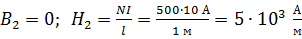 . Эти точки с вычисленными координатами: т. 1 (0; 0,63 Тл) и т. 2 (
. Эти точки с вычисленными координатами: т. 1 (0; 0,63 Тл) и т. 2 ( 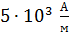 ; 0), – нанесем на поле графика и проведем прямую 1–2, которая описывается уравнением (2). Решением системы двух зависимостей, представленных на графике, является их общая точка – точка пересечения линий. Эта точка имеет следующие координаты (см. рис. 92):
; 0), – нанесем на поле графика и проведем прямую 1–2, которая описывается уравнением (2). Решением системы двух зависимостей, представленных на графике, является их общая точка – точка пересечения линий. Эта точка имеет следующие координаты (см. рис. 92): 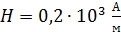 ;
; 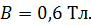
Дата: 2018-11-18, просмотров: 664.
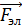
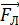
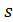
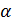
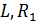
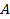
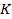
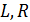
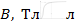
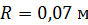 ;
;