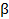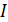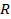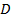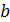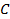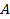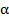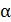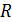План решения задач
1. В тех задачах, где магнитное поле создается током, текущим в проводнике сложной формы, проводник мысленно разбивают на отрезки (прямые или участки кругового контура), для которых известны расчетные формулы магнитной индукции. Затем записывают принцип суперпозиции магнитных полей в виде:
, (1)
где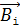 
– индукция магнитного поля отдельных i-тых отрезков проводника. По формуле (1) определяют также результирующее поле, созданное двумя и более длинными прямыми проводами или витками с током.
2. Для расчета магнитной индукции 
кругового тока в его центре или в точке на оси витка принцип суперпозиции записывают в следующем виде:
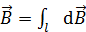. (2)
Здесь интегрирование выполняют по всей длине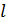 
проводника с током. Вектор 
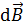определяют по закону Био – Савара – Лапласа. При сложении бесконечно малых векторов 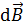возможны два варианта: 1) векторы 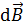сонаправлены, т. е. направлены по одной прямой; в этом случае модуль 
(суммируют модули 
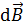); 2) если векторы не сонаправлены, то каждый из них необходимо разложить на два взаимно перпендикулярных вектора:
, (3)
где 
– вектор, параллельный оси витка с током; 
– составляющая вектора 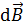, перпендикулярная оси витка.
3. В уравнениях (1) и (2) принципа суперпозиции записана суммавекторов. Для сложения векторов необходимо определить их направления и показать векторы на рисунке. Так как линии магнитного поля токов представляют собой окружности, замкнутые вокруг токов и даже вокруг бесконечно малых элементов тока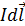 
, то используем правило буравчика, располагая винт вдоль тока. Если проводник с током размещен в плоскости рисунка, то в точках, находящихся в этой плоскости, вектор будет направлен перпендикулярно плоскости рисунка. Такой вектор обозначают значком 
, если вектор направлен «от нас», или значком €, если вектор направлен «к нам».
Задача 27. По тонкому кольцу радиусом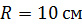 
течет ток 
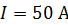. Определите магнитную индукцию в точке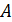 
на оси кольца, равноудаленной от точек кольца на расстояние 
.
Дано Решение
 ;
;
 .
|
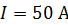Рис. 58 |
Мысленно разделим кольцо с током на элементы тока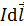 
, каждый из которых создает в точке 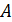магнитное поле с индукцией 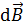, и сложим эти поля от элементов тока, согласно принципу суперпозиции:
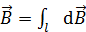. (1)
Здесь интегрирование выполняют по всей длине кольца 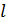, а вектор 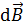определяется законом Био – Савара – Лапласа:
(2)
Из уравнения (2), в соответствии с векторным произведением векторов, следует, что вектор 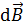перпендикулярен векторам 
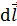и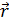 
. На рис. 58 плоскость кольца и элемент тока 
перпендикулярны плоскости рисунка. Следовательно, вектор 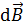будет расположен в плоскости рисунка, где его проводим перпендикулярно радиус-вектору 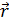, проведенному от элемента тока к точке 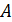. Выделим другой элемент тока 
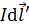, диаметрально противоположный элементу 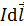, и покажем создаваемый им вектор магнитной индукции 
на рис. 58. Нетрудно заметить, что векторы 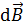от всех элементов тока кольца образуют конус векторов.
Для сложения векторов 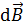, направленных по образующим конуса, разложим каждый вектор на две составляющие:
(3)
где – вектор, параллельный оси кольца ОА; – составляющая вектора 
, перпендикулярная оси кольца. После подстановки разложения (3) в уравнение (1) принципа суперпозиции интеграл в правой части представится суммой двух интегралов:
(4)
Второй интеграл: 
, так как сумма векторов 
и таким образом все векторы попарно компенсируются. Тогда в уравнении (4) остается один интеграл:
, (5)
где все векторы сонаправлены, следовательно, в точке 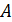вектор магнитной индукции 
(см. рис. 58), и его модуль
, (6)
Здесь составляющая 
, где 
(см. треугольники на рис. 58). Модуль находим с помощью закона Био – Савара – Лапласа (2): так как вектор 
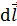, то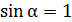 
и величина магнитной индукции
(7)
Подставим величину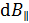 
в интеграл (6) и вычислим его:
(8)
Учтем, что 
– магнитный момент контура с током, и формулу (8) представим в виде
(9)
Вычисляем магнитную индукцию 
поля в точке 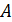по формуле (8), полагая, что для воздуха магнитная проницаемость 
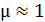, а магнитная постоянная 
.
.
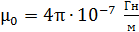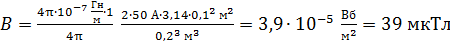Задача 28. По двум бесконечно длинным прямым параллельным проводам текут токи 
одного направления. Расстояние между проводами 
. Для линии 
, перпендикулярной проводам, определите, на каком участке: 1, 2 или 3 (рис. 59 а), – находится точка, в которой индукция магнитного поля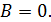 
На каком расстоянии 
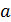от первого провода находится эта точка?
Дано Решение
 ;
 ;
1) 
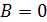на каком участке?
2) 
|
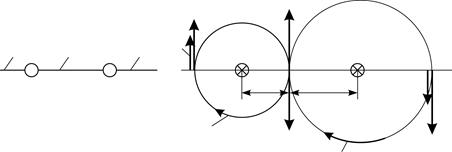
а б Рис. 59 |
Индукция магнитного поля в любой точке прямой определяется по принципу суперпозиции:
, (1)
где 
– магнитная индукция поля, созданного первым проводом с током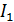 
; 
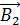– та же величина, созданная вторым проводом с током 
Так как в уравнении (1) записана геометрическая сумма векторов и 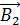, то определим их направления. Эти векторы направлены по касательным к линиям магнитной индукции, которые имеют форму окружностей с центрами на соответствующем проводе. Направление линий определяем по вращению головки буравчика (правого винта), который должен перемещаться по направлению тока. На рис. 59 б токи текут «от нас», поэтому буравчик следует вращать по часовой стрелке, чтобы винт вворачивался.
В каждой области (1, 2 и 3) показываем направление векторов и 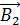, касательных к соответствующим окружностям. На участках 1 и 3 вектор 
, и сумма таких векторов отлична от нуля. На втором участке линии , который находится между проводами, вектор 
(см. рис. 59 б). Принимая за положительное направление вектора , запишем для этого участка принцип суперпозиции (1) в следующем виде:
(2)
Здесь модули магнитной индукции длинных прямых проводов определяем по формулам
(3)
Подставляем эти значения 
в уравнение (2) и, согласно условию задачи, приравниваем нулю индукцию результирующего магнитного поля:
(4)
Учитывая, что 
, из соотношения (4) определяем величину :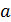
.
Таким образом, точка 
, в которой модули векторов одинаковы: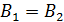 
,–а их сумма равна нулю, находится на отрезке прямой между проводами, ближе к первому проводу, – с меньшим током, так как величина 
.
Задача 29. По двум бесконечно длинным прямым проводам, скрещенным под прямым углом, текут токи 
, где 
Определите магнитную индукцию в точке 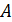(рис. 60 а), если расстояние 
Дано Решение
;
 ;
 ;
|
а б в Рис. 60 |
Магнитное поле, созданное двумя проводами с током, в любой точке пространства определяется по принципу суперпозиции как геометрическая сумма векторов:
, (1)
где и 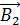– величины индукции магнитного поля, созданного первым проводом с током 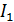и вторым – с током 
.
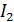Векторы и 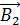направляем по касательным к линиям магнитной индукции. Эти линии – окружности с центрами на проводах с током, а направление линий (рис. 60 б) определяем по правилу буравчика (см. п. 7.1) Так как векторы и 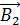взаимно перпендикулярны (рис. 60 в), то модуль магнитной индукции результирующего поля определяем с помощью теоремы Пифагора:
(2)
Модуль магнитной индукции поля, созданного длинным прямым проводником с током 
, рассчитывается по следующей формуле:
, (3)
где 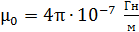– магнитная постоянная, 
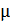– магнитная проницаемость среды, для воздуха ; 
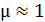– расстояние от провода до точки 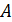, в которой определяем магнитную индукцию. Для первого и второго провода соответственно по формуле (3) запишем
(4)
Подставляя эти величины в выражение (2), получаем расчетную формулу для индукции магнитного поля в точке :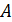
(5)
Вычисляем значение магнитной индукции поля в точке :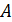
.
Задача 30. По двум бесконечно длинным прямым параллельным проводникам текут токи 
и 
. Определите магнитную индукцию поля в точке 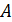(рис. 61 а), равноудаленной от проводов на расстояние 
; угол 
.
Дано Решение
| ;
;
;
.
|
а б Рис. 61 |
Так как магнитное поле создается двумя проводниками с током, то магнитную индукцию поля в точке 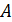определяем по принципу суперпозиции:
, (1)
где – индукция МП, созданная в точке 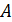первым проводником с током 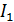; 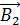– та же величина, созданная вторым проводником с током
Для сложения векторов и 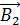необходимо показать их на рисунке. Эти векторы идут по касательным к линиям магнитной индукции, которые представляют собой окружности радиусом 
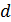, охватывающие первый и второй проводники. Касательные проводим перпендикулярно радиусу 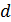соответствующей окружности (рис. 61 б).
Результирующий вектор , согласно принципу суперпозиции (1), находим по правилу параллелограмма (треугольника). Модуль его определяем по теореме косинусов:
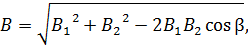(2)
где угол 
(так как ( 
, (см. рис. 61 б)). Модули магнитной индукции поля, созданного первым и вторым проводниками, определяются формулами:
(3)
Здесь магнитная проницаемость воздуха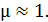 
Подставляем эти величины в уравнение (2) и получаем расчетную формулу индукции МП в точке 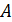в следующем виде:
; так как 
.
Вычисляем величину магнитной индукции поля в точке :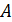
.
Задача 31. По бесконечно длинному проводнику, изогнутому так, как показано на рис. 62 а, течет ток . Радиус дуги 
. Определите магнитную индукцию в точке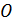 
.
Дано Решение
;
|
а б Рис. 62 |
Провод заданной формы разделим на три участка (рис. 62 б): длинные прямые проводники 1 и 3 и дуга 2, равная половине окружности. Индукцию 
, созданного проводником, состоящим из таких участков, найдем по принципу суперпозиции:
(1)
Вычислим вектор от первого участка проводника, суммируя бесконечно малые значения 
, создаваемые элементами тока 
:
, (2)
где вектор определяем по закону Био – Савара – Лапласа:
. (3)
В формуле закона (3) элемент длины 
первого участка провода и радиус-вектор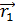 
, проведенный от элемента тока к точке 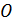, сонаправлены, т. е. 
, а в этом случае векторное произведение 
(так как 
). Следовательно, каждый 
и их сумма 
Отметим полученный результат: в любой точке, находящейся на продолжении прямого провода с током, индукция МП, созданная этим проводом, равна нулю.
Вычислим вектор 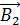, аналогично предыдущему расчету, суммируя бесконечно малые значения 
, создаваемые элементами тока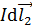 
:
. (4)
Для определения направления складываемых векторов применяем правило буравчика: вращая головку винта по направлению тока в полукольце, по движению винта (который будет ввинчиваться) получаем, что вектор от любого элемента тока дуги направлен перпендикулярно плоскости рисунка «от нас». Следовательно, и вектор 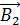имеет такое же направление. Так как все векторы сонаправлены, то суммируем их модули:
(5)
Отметим, что найденная величина 
(см. п. 7.1, формула (6)). Этот результат имеет простое объяснение: отсутствующая половина кольца создавала бы такое же поле 
, а согласно принципу суперпозиции 
. Следовательно, расчет выполнен верно.
Определяем вектор 
: его направление находим по правилу буравчика, вращая головку винта по часовой стрелке (если смотреть на начало третьего участка сверху), чтобы винт вворачивался по направлению тока (вниз). Тогда вектор , касательный к окружности, которую описывает головка винта, будет направлен перпендикулярно плоскости рисунка «от нас». Таким образом, вектор 
; складывая эти векторы, по принципу суперпозиции (1) получаем, что результирующий вектор сонаправлен с векторами 
, т. е. также направлен перпендикулярно плоскости рисунка «от нас». Модуль вектора , в соответствии с уравнением (1), равен сумме модулей сонаправленных векторов:
(6)
Найдем модуль вектора . Заметим, что если мысленно продолжить участок провода 3 вверх до бесконечности, т. е. дополнить его проводом, равным участку 3, то получим бесконечно длинный прямой провод, создающий поле с магнитной индукцией
. (7)
С учетом равного вклада двух половин провода, следуя принципу суперпозиции, запишем уравнение:
(8)
Заметим, что результат (8) можно получить и из формулы магнитной индукции отрезка прямого проводника с током (п. 7.1, формула (8)):
, (9)
где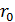 
– расстояние от провода до точки, в которой определяем величину : 
; углы 
, т. е. 
Подставляя найденные величины магнитной индукции второго и третьего участков провода (формулы (5) и (8)) в уравнение (6) принципа суперпозиции, получаем расчетную формулу индукции магнитного поля в точке :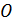
(10)
Вычисляем магнитную индукцию поля, созданного в точке 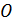заданным проводником с током, по формуле (10), принимая для воздуха магнитную проницаемость 
.
Дата: 2018-11-18, просмотров: 411.
