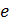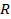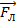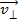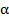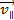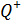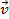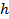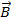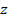В электрическом и магнитном полях
План решения задач
1. Решение следует начинать с рисунка, на котором необходимо показать направление силовых характеристик полей – напряженности электростатического поля 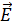 и магнитной индукции
и магнитной индукции  . Затем, в соответствии с формулой Лоренца:
. Затем, в соответствии с формулой Лоренца:
 (1)
(1)
нужно показать направление электрической силы 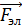 и магнитной –
и магнитной –  (это сила Лоренца
(это сила Лоренца 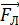 ).
).
2. Направление сил определяем в соответствии с формулой (1):  , а сила Лоренца определяется по правилу левой руки: располагая руку так, чтобы линии магнитной индукции
, а сила Лоренца определяется по правилу левой руки: располагая руку так, чтобы линии магнитной индукции  входили в ладонь, четыре пальца направить вдоль скорости частицы
входили в ладонь, четыре пальца направить вдоль скорости частицы 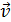 , тогда отогнутый большой палец покажет направление силы
, тогда отогнутый большой палец покажет направление силы 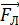 . Но следует иметь в виду, что в формуле (1) заряд частицы
. Но следует иметь в виду, что в формуле (1) заряд частицы  записывается со своим знаком; следовательно, для отрицательно заряженной частицы
записывается со своим знаком; следовательно, для отрицательно заряженной частицы  , а сила Лоренца, определенная по правилу левой руки для положительно заряженных частиц, в случае отрицательного заряда будет направлена противоположно найденной силе.
, а сила Лоренца, определенная по правилу левой руки для положительно заряженных частиц, в случае отрицательного заряда будет направлена противоположно найденной силе.
3. На рисунке необходимо показать также траекторию движения частицы. Она обычно задана в условии задачи: 1) либо оговорена явно, например, частица движется прямолинейно, или найти силу эквивалентного кругового тока, или дан шаг винтовой линии; 2) или указана неявно. В этом втором случае задается угол 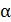 между векторами скорости частицы
между векторами скорости частицы 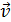 и магнитной индукции
и магнитной индукции  . Этих данных достаточно, чтобы определить величину силы Лоренца, которая создает нормальное (центростремительное) ускорение частицы (см. п. 7.3).
. Этих данных достаточно, чтобы определить величину силы Лоренца, которая создает нормальное (центростремительное) ускорение частицы (см. п. 7.3).
4. Заметим, что для элементарных частиц: электрона и протона, – а также и для ионов, действующая на них сила тяжести  мала по сравнению с электрической и магнитной силами. Поэтому ее опускают в уравнениях движения заряженных частиц в электрических и магнитных полях.
мала по сравнению с электрической и магнитной силами. Поэтому ее опускают в уравнениях движения заряженных частиц в электрических и магнитных полях.
Задача 38. Однозарядный ион прошел ускоряющую разность потенциалов  и влетел перпендикулярно линиям магнитной индукции в однородное магнитное поле с индукцией
и влетел перпендикулярно линиям магнитной индукции в однородное магнитное поле с индукцией 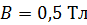 . В магнитном поле ион начал движение по окружности радиусом
. В магнитном поле ион начал движение по окружности радиусом  . Определите удельный заряд иона
. Определите удельный заряд иона 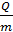 и его относительную атомную массу
и его относительную атомную массу 
Дано Решение
 ; ;
 ; ;
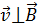 ; ;
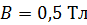 ; ;
 . .
 ? ?
|
|

Рис. 69 |
При движении заряженной частицы в электростатическом поле оно совершает работу
 , (1)
, (1)
ускоряя заряженную частицу – ион. Работа сил поля идет на приращение кинетической энергии иона:
 (2)
(2)
Принимая, что начальная энергия иона  , и объединяя формулы (1) и (2), запишем следующее равенство:
, и объединяя формулы (1) и (2), запишем следующее равенство:
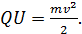 (3)
(3)
Из формулы (3) находим скорость иона:
 (4)
(4)
Ион, движущийся с приобретенной в ЭСП скоростью 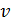 , в магнитном поле испытывает действие силы Лоренца:
, в магнитном поле испытывает действие силы Лоренца:

Направление вектора силы 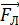 определяем по правилу левой руки (рис. 69), располагая ладонь руки в плоскости рисунка. Так как по условию задачи вектор скорости
определяем по правилу левой руки (рис. 69), располагая ладонь руки в плоскости рисунка. Так как по условию задачи вектор скорости 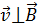 , т. е. угол между этими векторами
, т. е. угол между этими векторами 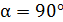 , то
, то 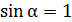 и модуль силы Лоренца
и модуль силы Лоренца
 (5)
(5)
Сила Лоренца, перпендикулярная скорости движения иона, сообщает частице нормальное, или центростремительное ускорение  . Эта центростремительная сила направлена к центру окружности, а вектор скорости
. Эта центростремительная сила направлена к центру окружности, а вектор скорости 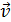 – по касательной к окружности; такая траектория показана на рисунке (см. рис. 69). Согласно второму закону Ньютона:
– по касательной к окружности; такая траектория показана на рисунке (см. рис. 69). Согласно второму закону Ньютона:

Запишем проекцию уравнения этого закона на нормаль к траектории, подставляя величину нормального ускорения 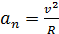 и силу Лоренца по формуле (5):
и силу Лоренца по формуле (5):
 (6)
(6)
Приравняем скорость, полученную ионом в электрическом поле, – по формуле (3) и величину скорости, соответствующую заданной окружности в магнитном поле, – по формуле (6):
 .
.
Из последнего равенства выражаем удельный заряд иона:
 (7)
(7)
Вычисляем величину удельного заряда иона по формуле (7):
 .
.
Найдем массу иона, учитывая, что удельный заряд данного иона
 ;
;  .
.
Вычисляем массу иона:
 .
.
Выразим массу иона в атомных единицах массы, учитывая, что 1 а.е.м.  :
:
 .
.
Найденная относительная атомная масса показывает, что это ион калия 
Задача 39. Электрон влетает со скоростью  в однородное магнитное поле с индукцией
в однородное магнитное поле с индукцией  перпендикулярно линиям магнитной индукции. Определите период
перпендикулярно линиям магнитной индукции. Определите период  обращения электрона, силу эквивалентного кругового тока
обращения электрона, силу эквивалентного кругового тока  и магнитный момент
и магнитный момент 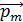 этого тока.
этого тока.
Дано Решение
Электрон:
 ; ;
 ; ;
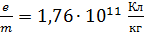 ; ;
 ; ;
 . .

|

а б Рис. 70 |
Рассмотрим движение электрона в магнитном поле. На электрон действует сила Лоренца
 , (1)
, (1)
направление которой находим по правилу левой руки с учетом знака заряда. Направление силы, полученное по этому правилу для заряда  , изменяем на противоположное, так как электрон имеет отрицательный заряд. Чтобы траектория движения электрона располагалась в плоскости рисунка, вектор магнитной индукции
, изменяем на противоположное, так как электрон имеет отрицательный заряд. Чтобы траектория движения электрона располагалась в плоскости рисунка, вектор магнитной индукции  направим перпендикулярно этой плоскости (рис. 70 а). Показав на рисунке векторы скорости
направим перпендикулярно этой плоскости (рис. 70 а). Показав на рисунке векторы скорости 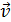 и силы Лоренца
и силы Лоренца 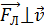 , изображаем траекторию движения электрона. При этом окружность проводим так, чтобы сила Лоренца, которая является центростремительной, была направлена к центру окружности, а скорость частицы
, изображаем траекторию движения электрона. При этом окружность проводим так, чтобы сила Лоренца, которая является центростремительной, была направлена к центру окружности, а скорость частицы 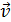 – по касательной к траектории. Сила Лоренца сообщает электрону нормальное (центростремительное) ускорение
– по касательной к траектории. Сила Лоренца сообщает электрону нормальное (центростремительное) ускорение 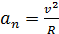 . Запишем второй закон Ньютона в проекции на нормаль к траектории:
. Запишем второй закон Ньютона в проекции на нормаль к траектории:
 . (2)
. (2)
Здесь 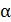 – угол между векторами скорости
– угол между векторами скорости 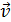 и магнитной индукции
и магнитной индукции  ; по условию задачи
; по условию задачи 
Период обращения электрона 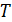 – время одного оборота, найдем из формулы пути
– время одного оборота, найдем из формулы пути  для равномерного движения электрона по окружности:
для равномерного движения электрона по окружности:
 (3)
(3)
Необходимое для расчета отношение радиуса окружности 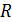 к скорости частицы
к скорости частицы 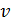 выразим из закона динамики (2):
выразим из закона динамики (2):
 (4)
(4)
После подстановки выражения (4) в формулу (3) получаем расчетную формулу величины периода обращения электрона в магнитном поле:
 (5)
(5)
Вычисляем величину периода обращения частицы:
 .
.
Силу эквивалентного кругового тока, создаваемого движением электрона, найдем, используя определительную формулу величины постоянного тока:  , где
, где 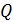 – заряд, перенесенный через сечение проводника за время
– заряд, перенесенный через сечение проводника за время 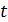 . Для этого мысленно поместим на круговую орбиту электрона проводник и заметим, что за время, равное периоду обращения, электрон переносит свой заряд, равный
. Для этого мысленно поместим на круговую орбиту электрона проводник и заметим, что за время, равное периоду обращения, электрон переносит свой заряд, равный  При этом соответствующий ток
При этом соответствующий ток
 (6)
(6)
Вычисляем силу эквивалентного кругового тока, отметив, что его направление, показанное на рис. 70 а, – против часовой стрелки, противоположно скорости движения электрона, так как за направление тока принимают направление скорости движения положительных зарядов:
 .
.
Магнитный момент эквивалентного кругового тока находим по определительной формуле:
 , (7)
, (7)
где  – ток в контуре;
– ток в контуре; 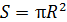 – площадь, ограниченная контуром,
– площадь, ограниченная контуром, 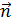 – единичная нормаль к площади контура, ее направление связано с направлением тока
– единичная нормаль к площади контура, ее направление связано с направлением тока  правилом правого винта (буравчика). В нашем случае векторы
правилом правого винта (буравчика). В нашем случае векторы 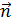 и магнитный момент
и магнитный момент  направлены перпендикулярно плоскости, в которой расположены траектория электрона и круговой ток
направлены перпендикулярно плоскости, в которой расположены траектория электрона и круговой ток  (рис. 70 б).
(рис. 70 б).
Подставляя в формулу (7) величину тока  по формуле (6) и радиус окружности, выраженный из формулы (4), получим расчетную формулу магнитного момента эквивалентного кругового тока в следующем виде:
по формуле (6) и радиус окружности, выраженный из формулы (4), получим расчетную формулу магнитного момента эквивалентного кругового тока в следующем виде:
 .
.
Вычисляем величину магнитного момента кругового тока, созданного движением электрона в магнитном поле:
 .
.
Задача 40. Протон со скоростью  влетает в однородное магнитное поле с индукцией
влетает в однородное магнитное поле с индукцией  . Вектор скорости протона направлен под углом
. Вектор скорости протона направлен под углом  к линиям магнитной индукции. Определите радиус
к линиям магнитной индукции. Определите радиус 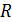 и шаг
и шаг  винтовой линии, по которой движется протон.
винтовой линии, по которой движется протон.
|
Протон:
 ; ;
 ; ;
 ; ;
 ; ;
 . .
 
|

Рис. 71 |
Для описания движения протона удобно представить вектор его скорости 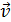 как сумму двух составляющих, одна из которых –
как сумму двух составляющих, одна из которых –  направлена вдоль линий индукции магнитного поля
направлена вдоль линий индукции магнитного поля  , а вторая –
, а вторая –  перпендикулярна им (рис. 71). Тогда сила Лоренца, действующая на протон, запишется в следующем виде:
перпендикулярна им (рис. 71). Тогда сила Лоренца, действующая на протон, запишется в следующем виде:
 , (1)
, (1)
так как для коллинеарных векторов  величина
величина  . Следовательно, составляющая скорости
. Следовательно, составляющая скорости  , т. е. не изменяется ни по модулю, ни по направлению. С этой скоростью протон будет двигаться равномерно и прямолинейно вдоль линий магнитного поля
, т. е. не изменяется ни по модулю, ни по направлению. С этой скоростью протон будет двигаться равномерно и прямолинейно вдоль линий магнитного поля 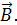 Составляющая скорости
Составляющая скорости 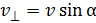 (см. рис. 71) остается постоянной по модулю, но непрерывно изменяет свое направление под действием силы Лоренца, так как эта сила сообщает протону центростремительное ускорение.
(см. рис. 71) остается постоянной по модулю, но непрерывно изменяет свое направление под действием силы Лоренца, так как эта сила сообщает протону центростремительное ускорение.
Таким образом, протон участвует в двух движениях: равномерном и прямолинейном со скоростью 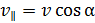 параллельно линиям индукции МП и во вращательном движении в плоскости, перпендикулярной линиям магнитной индукции. В результате наложения этих двух независимых движений траекторией протона будет винтовая линия.
параллельно линиям индукции МП и во вращательном движении в плоскости, перпендикулярной линиям магнитной индукции. В результате наложения этих двух независимых движений траекторией протона будет винтовая линия.
Для определения радиуса винтовой линии применим второй закон Ньютона в проекции на нормаль к окружности витка:
 (2)
(2)
Подставляя составляющую скорости протона 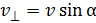 , выразим радиус
, выразим радиус
 (3)
(3)
Вычисляем величину радиуса винтовой линии
 .
.
Шаг винтовой линии 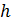 находим по формуле пути при равномерном прямолинейном движении:
находим по формуле пути при равномерном прямолинейном движении:
 , (4)
, (4)
где 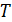 – период обращения (время одного оборота). Чтобы найти величину периода, запишем формулу пути
– период обращения (время одного оборота). Чтобы найти величину периода, запишем формулу пути  для равномерного движения протона по окружности со скоростью
для равномерного движения протона по окружности со скоростью 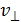 :
:
 (5)
(5)
Подставляя величину радиуса окружности по формуле (3), получаем период обращения протона в магнитном поле:
 (6)
(6)
С учетом этого выражения формула (4) преобразуется в следующую расчетную формулу шага винтовой линии:

 (7)
(7)
Вычисляем величину 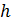 :
:
 .
.
Задача 41. Альфа-частица со скоростью  влетает в скрещенные под прямым углом электростатическое и магнитное поля. Напряженность электрического поля
влетает в скрещенные под прямым углом электростатическое и магнитное поля. Напряженность электрического поля  , магнитная индукция
, магнитная индукция  Определите ускорение
Определите ускорение 
 -частицы в момент вхождения ее в область пространства, где существуют поля. Скорость частицы перпендикулярна векторам
-частицы в момент вхождения ее в область пространства, где существуют поля. Скорость частицы перпендикулярна векторам  и
и 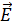 , а силы, действующие на
, а силы, действующие на 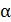 -частицу со стороны этих полей, направлены противоположно друг другу.
-частицу со стороны этих полей, направлены противоположно друг другу.
Дано Решение
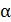 -частица ( -частица (  : :
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 и и 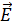 ); );
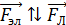 . .
 ? ?
|

Рис. 72 |
Показываем на рис. 72 направление силовых характеристик полей  и
и 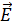 , в соответствии с условием задачи, и направление электрической и магнитной сил:
, в соответствии с условием задачи, и направление электрической и магнитной сил:  , поэтому
, поэтому  , так как заряд
, так как заряд 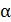 -частицы положительный;
-частицы положительный;  по условию задачи. После этого определяем направление вектора скорости частицы
по условию задачи. После этого определяем направление вектора скорости частицы 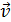 – оно должно быть таково, чтобы по правилу левой руки получить направление силы Лоренца, которая уже показана, как направленная противоположно электрической силе (см. рис. 72).
– оно должно быть таково, чтобы по правилу левой руки получить направление силы Лоренца, которая уже показана, как направленная противоположно электрической силе (см. рис. 72).
Записываем формулу Лоренца для силы, действующей на заряженную частицу в электрическом и магнитном полях:
 (1)
(1)
Эта формула отражает принцип суперпозиции сил (независимости их действия). Проекция силы 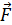 на ось
на ось 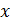 , которая выбрана параллельной вектору напряженности электрического поля
, которая выбрана параллельной вектору напряженности электрического поля 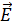 , запишется в виде:
, запишется в виде:
 (2)
(2)
Здесь при записи модуля силы Лоренца учтено, что вектор 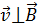 , поэтому
, поэтому 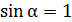 .
.
Проекцию ускорения на ось 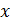 определим по второму закону Ньютона:
определим по второму закону Ньютона:
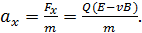 (3)
(3)
Вычисляем ускорение, учитывая, что 1 а.е.м.  :
:
 .
.
Проекция ускорения альфа-частицы на ось 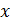 положительна, следовательно, ускорение частицы направлено вдоль оси
положительна, следовательно, ускорение частицы направлено вдоль оси 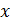 и совпадает по направлению с электрической силой, которая по модулю больше, чем магнитная, в условиях данной задачи.
и совпадает по направлению с электрической силой, которая по модулю больше, чем магнитная, в условиях данной задачи.
Задача 42. В скрещенные под прямым углом однородные электрическое и магнитное поля влетает ион. Напряженность магнитного поля 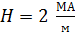 , а напряженность электростатического поля
, а напряженность электростатического поля  . Определите величину и направление вектора скорости
. Определите величину и направление вектора скорости 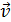 , при которых движение иона в этих полях будет прямолинейным и равномерным.
, при которых движение иона в этих полях будет прямолинейным и равномерным.
|
 ; ;
 . .

|

Рис.73 |
В области пространства, где совмещены электрическое и магнитное поля, на движущийся ион действуют две силы: электрическая 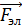 и магнитная – сила Лоренца
и магнитная – сила Лоренца 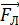 . Для положительно заряженного иона электрическая сила сонаправлена с напряженностью электрического поля:
. Для положительно заряженного иона электрическая сила сонаправлена с напряженностью электрического поля:  (рис. 73), так как эта сила
(рис. 73), так как эта сила
 . (1)
. (1)
Сила Лоренца определяется формулой
 (2)
(2)
При прямолинейном равномерном движении иона его скорость  , а ускорение
, а ускорение  . Следовательно, в соответствии со вторым законом Ньютона:
. Следовательно, в соответствии со вторым законом Ньютона:  , – необходимо, чтобы результирующая сила
, – необходимо, чтобы результирующая сила 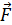 , действующая на заряженную частицу со стороны обоих полей, была равна нулю, т. е. действие электрической и магнитной сил должно быть взаимно скомпенсировано:
, действующая на заряженную частицу со стороны обоих полей, была равна нулю, т. е. действие электрической и магнитной сил должно быть взаимно скомпенсировано:
 (3)
(3)
Соответственно, направляем вектор силы Лоренца  (см. рис. 73). Вектор скорости иона
(см. рис. 73). Вектор скорости иона 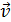 направлен вдоль линии, перпендикулярной вектору силы Лоренца, так как, согласно векторному произведению (2),
направлен вдоль линии, перпендикулярной вектору силы Лоренца, так как, согласно векторному произведению (2), 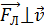 . Из двух линий, перпендикулярных оси
. Из двух линий, перпендикулярных оси 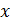 , вдоль которой направлена сила Лоренца, выбираем для скорости ось
, вдоль которой направлена сила Лоренца, выбираем для скорости ось 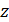 , а не
, а не 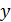 , так как в случае
, так как в случае  сила Лоренца обратилась бы в нуль (см. формулу (2)). Вектор
сила Лоренца обратилась бы в нуль (см. формулу (2)). Вектор 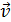 направим в положительном направлении оси
направим в положительном направлении оси 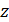 , чтобы по правилу левой руки получить заданное направление силы Лоренца (см. рис. 73).
, чтобы по правилу левой руки получить заданное направление силы Лоренца (см. рис. 73).
В соответствии с формулой (3), приравниваем модули электрической и магнитной сил:
 (4)
(4)
Здесь в векторном произведении 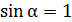 , так как скорость частицы
, так как скорость частицы 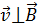 (см. рис. 73). Из равенства (4) выражаем искомую величину скорости иона:
(см. рис. 73). Из равенства (4) выражаем искомую величину скорости иона:
 или
или  . (5)
. (5)
Здесь магнитная проницаемость вакуума 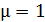 , так как только в вакууме возможно движение ионов без соударений с молекулами среды – воздуха.
, так как только в вакууме возможно движение ионов без соударений с молекулами среды – воздуха.
Вычисляем скорость иона по расчетной формуле (5):
 .
.
Отметим, что рассмотренное выше движение ионов в скрещенных электрическом и магнитном полях используется в фильтре скоростей, который обычно является составной частью масс-спектрометров и других приборов и устройств. Фильтр предназначен для выделения из пучка ионов частиц с определенной скоростью, величину которой можно рассчитать, как это сделано в решении данной задачи.
Дата: 2018-11-18, просмотров: 699.