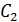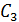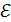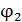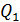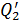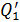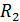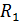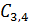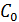План решения задач
1) Прежде всего, необходимо изобразить на рисунке схему соединения конденсаторов согласно условию задачи. Если конденсаторов несколько и приведена схема их соединения, то в ней нужно выделить группы конденсаторов, соединенных параллельно. Признаки параллельного соединения: а) одинаковая разность потенциалов на выделенных группах (или одинаковый потенциал обкладок, при этом крайние конденсаторы групп соединены одноименно заряженными обкладками); б) заряд батареи, который подводится при ее зарядке от источника тока (или отводится при разряде батареи), равен сумме зарядов параллельно соединенных групп конденсаторов. Например, в схеме, приведенной на рис. 34, конденсаторы 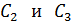 соединены последовательно
соединены последовательно 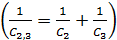 . Группа этих двух
. Группа этих двух
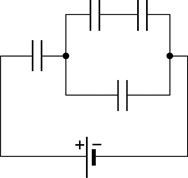
Рис.34 |
конденсаторов емкостью  соединена параллельно с конденсатором емкостью
соединена параллельно с конденсатором емкостью 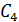 . Но конденсатор емкостью
. Но конденсатор емкостью 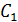 соединен последовательно с группой конденсаторов
соединен последовательно с группой конденсаторов 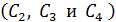 , емкость которой равна
, емкость которой равна 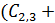
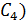 .
.
2) В случае соединения двух предварительно заряженных проводников или конденсаторов, а также при подключении незаряженного проводника (конденсатора) к заряженному проводнику происходит перераспределение зарядов между проводниками или обкладками конденсаторов. При этом обязательно выполняется закон сохранения электрического заряда (ЗСЗ), так как соединяемые проводники (конденсаторы), окруженные слоем диэлектрика – воздуха, образуют замкнутую (электрически изолированную) систему.
3) Суммарная энергия электростатических полей проводников (конденсаторов) до их соединения обычно больше энергии ЭСП после соединения проводников. Это согласуется с законом сохранения энергии, так как часть энергии начальных электростатических полей выделяется при протекании по проводникам тока перезарядки (преобразуется при их нагреве во внутреннюю энергию проводников), преимущественно, в слабо ионизированном воздухе путем образовании искры.
Задача 18. Два заряженных металлических шара, первый радиусом  , имеющий заряд
, имеющий заряд 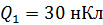 , а второй – радиусом
, а второй – радиусом 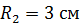 , имеющий потенциал
, имеющий потенциал  , соединили проводником, емкостью которого можно пренебречь. Определите 1) заряд второго шара до соединения шаров, 2) потенциал шаров
, соединили проводником, емкостью которого можно пренебречь. Определите 1) заряд второго шара до соединения шаров, 2) потенциал шаров 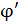 после их соединения, 3) энергии
после их соединения, 3) энергии 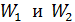 каждого шара до соединения, 4) их энергии
каждого шара до соединения, 4) их энергии 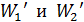 после соединения шаров.
после соединения шаров.
Дано Решение
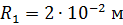 ; ;
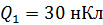 ; ;
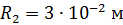 ; ;
 ; ;
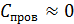 . .
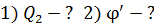 3)
3) 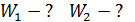 4)
4) 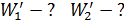
|
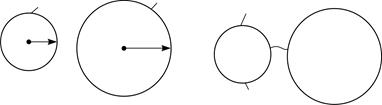
а б Рис. 35 |
1) Условия статического равновесия свободных электронов в заряженном проводнике: а) напряженность ЭСП 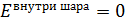 (только при этом электрическая сила, действующая на электроны,
(только при этом электрическая сила, действующая на электроны, 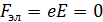 ); б) потенциал проводника
); б) потенциал проводника 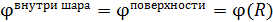 ; в) весь избыточный заряд находится на поверхности проводника. Таким образом, потенциал
; в) весь избыточный заряд находится на поверхности проводника. Таким образом, потенциал 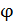 металлического шара равен потенциалу сферы, равномерно заряженной по поверхности:
металлического шара равен потенциалу сферы, равномерно заряженной по поверхности:
 (1)
(1)
где 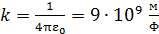 – коэффициент пропорциональности в законе Кулона;
– коэффициент пропорциональности в законе Кулона; 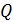 – заряд шара;
– заряд шара; 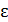 – диэлектрическая проницаемость среды (для воздуха
– диэлектрическая проницаемость среды (для воздуха 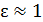 );
); 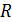 – радиус шара.
– радиус шара.
Заряд второго шара выразим из формулы (1):
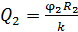 .
.
Вычисляем 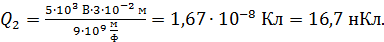
2) При соединении шаров (рис. 35) заряды на них перераспределяются так, чтобы образовался один эквипотенциальный проводник:
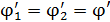 .
.
Иначе, если будет разность потенциалов между шарами, то будет протекать электрический ток, в соответствии с законом Ома:  , где
, где 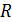 – сопротивление соединительного проводника.
– сопротивление соединительного проводника.
Потенциал шаров 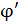 связан с их суммарным зарядом
связан с их суммарным зарядом 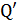 формулой
формулой
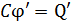 , (2)
, (2)
где 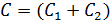 – электроемкость двух соединенных шаров, ее находим, как для параллельно соединенных конденсаторов, так как аналогично таковому, с поверхности соединенных шаров при их разряде отведется сумма зарядов шаров
– электроемкость двух соединенных шаров, ее находим, как для параллельно соединенных конденсаторов, так как аналогично таковому, с поверхности соединенных шаров при их разряде отведется сумма зарядов шаров 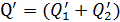 . Эту сумму найдем, используя закон сохранения заряда: сумма зарядов шаров до соединения равна суммарному заряду соединенных шаров:
. Эту сумму найдем, используя закон сохранения заряда: сумма зарядов шаров до соединения равна суммарному заряду соединенных шаров:
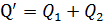 ;
;
(соединительный проводник практически не приобрел заряд, так как его емкость пренебрежимо мала: 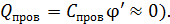 Подставим величину
Подставим величину 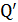 в формулу (2) и определим из нее потенциал шаров
в формулу (2) и определим из нее потенциал шаров
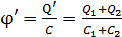 ; (3)
; (3)
Электроемкость шара найдем по определительной формуле, используя значение потенциала шара, определяемое формулой (1):
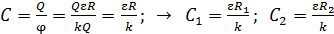 . (4)
. (4)
Эти значения емкости шаров подставим в формулу (3), принимая для воздуха 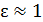 :
:
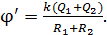 (5)
(5)
Вычисляем по формуле (5) потенциал шаров после их соединения:
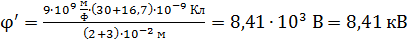 .
.
3) Значения энергии электростатического поля заряженных шаров до их соединения найдем по формуле
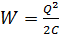 .
.
Подставляя величину емкости по формуле (4), получаем расчетные формулы:
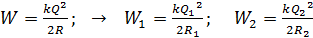 .
.
Вычисляем значения энергий ЭСП шаров до их соединения:
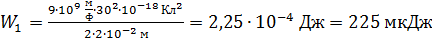 ;
;
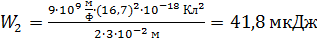 .
.
Значения энергии ЭСП соединенных шаров, потенциал которых равен 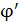 , найдем по следующей формуле:
, найдем по следующей формуле:
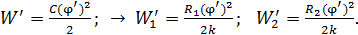 (7)
(7)
Вычисляем по этим формулам энергии соединенных шаров:
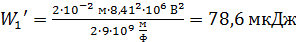 ;
;
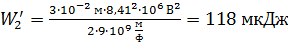 .
.
Используя закон сохранения энергии в следующем виде:
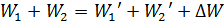 ,
,
определяем энергию 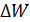 , которая пошла на образование искры шаров:
, которая пошла на образование искры шаров:
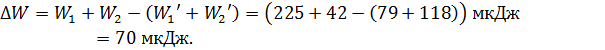
Таким образом, на образование искры в момент соединения затрачена часть энергии 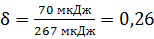 , (26%) от начальной энергии шаров.
, (26%) от начальной энергии шаров.
Задача 19. Конденсаторы емкостями 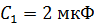 ,
,  ,
, 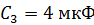 и
и 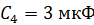 соединены так, как показано на рис. 36 а. Разность потенциалов между точками А и В
соединены так, как показано на рис. 36 а. Разность потенциалов между точками А и В 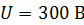 . Определите 1) заряд на пластинах каждого конденсатора, 2) заряд батареи конденсаторов и 3) разность потенциалов на каждом конденсаторе.
. Определите 1) заряд на пластинах каждого конденсатора, 2) заряд батареи конденсаторов и 3) разность потенциалов на каждом конденсаторе.
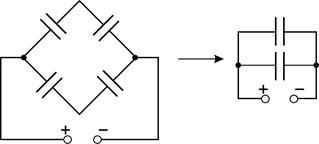
а б Рис. 36 |
Дано Решение
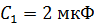 ; ;
 ; ;
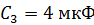 ; ;
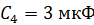 ; ;
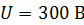 . .
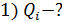 2) 2) 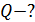 3)
3) 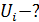 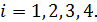
|
1) Конденсаторы емкостями 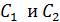 соединены между собой последовательно, поэтому заряд на их обкладках одинаков и равен заряду этого звена емкостью
соединены между собой последовательно, поэтому заряд на их обкладках одинаков и равен заряду этого звена емкостью 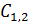 :
:
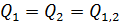 . (1)
. (1)
Для определения заряда на обкладках конденсаторов используем формулу
 (2)
(2)
где емкость 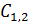 найдем по формуле последовательного соединения конденсаторов:
найдем по формуле последовательного соединения конденсаторов:
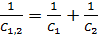 . (3)
. (3)
Вычислим 
Используя формулы (1) и (2), вычисляем заряд на обкладках этих конденсаторов:
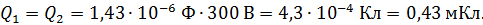
Аналогичный расчет выполняем для пары конденсаторов емкостями 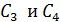 :
:
 .
.
Заряды на обкладках конденсаторов
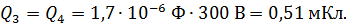
2) Из эквивалентной схемы электрической цепи (рис. 36 б) следует, что при параллельном соединении звеньев емкостями 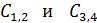 электроемкость всей цепи
электроемкость всей цепи
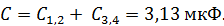
По формуле (2) вычисляем заряд, который можно отвести с этой батареи конденсаторов

Отметим, что этот заряд 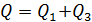 (см. рис. 36 б).
(см. рис. 36 б).
3) Напряжение на каждом конденсаторе найдем с помощью следующей формулы:
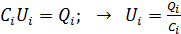 . (4)
. (4)
Вычисляем напряжение по полученной формуле:
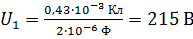 ;
; 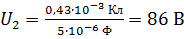 ;
;
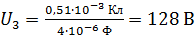 ;
; 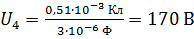 .
.
Отметим, что вычисленные напряжения на конденсаторах согласуются со схемой электрической цепи (см. рис. 36 а):
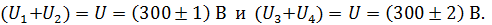
Задача 20. Между обкладками заряженного конденсатора вдвигается пластина диэлектрика с диэлектрической проницаемостью 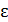 , плотно прилегающая к обкладкам. Сравните следующие величины до и после внесения диэлектрика: 1) заряды конденсатора
, плотно прилегающая к обкладкам. Сравните следующие величины до и после внесения диэлектрика: 1) заряды конденсатора  ; 2) разности потенциалов
; 2) разности потенциалов  ; 3) емкости конденсатора
; 3) емкости конденсатора 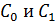 ; 4) напряженности
; 4) напряженности 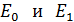 электростатического поля между пластинами; 5) энергии конденсатора
электростатического поля между пластинами; 5) энергии конденсатора 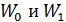 . Рассмотрите два случая: а) конденсатор отключен от источника тока; б) конденсатор подсоединен к источнику тока.
. Рассмотрите два случая: а) конденсатор отключен от источника тока; б) конденсатор подсоединен к источнику тока.
|
|
|
а) конденсатор отключен (рис. 37 а);
б) конденсатор подключен (рис. 37 б).
1) 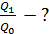 2) 2) 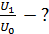 3) 3) 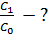 4)
4) 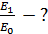 5) 5) 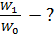
|
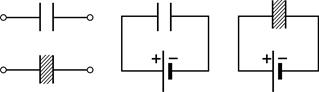
а б Рис. 37 |
а) Диэлектрическая пластина вдвигается в конденсатор, отключенный от источника тока (рис. 37 а).
1) Заряд обкладок конденсатора остается неизменным, так как обкладки электрически изолированы:
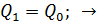
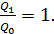
3) Электроемкость плоского конденсатора описывается формулой
 . (1)
. (1)
Согласно этой формуле, величина 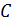 увеличится в
увеличится в 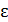 раз при внесении диэлектрика, так как для воздуха
раз при внесении диэлектрика, так как для воздуха  :
:
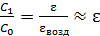 .
.
2) Напряжение на конденсаторе изменяется в соответствии с формулой
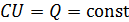 . (2)
. (2)
При увеличении емкости 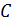 в
в 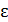 раз величина напряжения
раз величина напряжения 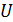 снизится в
снизится в 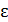 раз, чтобы произведение этих величин, равное заряду обкладок, не изменилось.
раз, чтобы произведение этих величин, равное заряду обкладок, не изменилось.
4) Для однородного электростатического поля в плоском конденсаторе напряженность поля
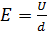 , (3)
, (3)
где 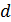 – расстояние между обкладками, оно остается неизменным. Согласно формуле (3), снижение напряжения
– расстояние между обкладками, оно остается неизменным. Согласно формуле (3), снижение напряжения 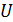 на конденсаторе в
на конденсаторе в 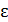 раз приведет к уменьшению напряженности ЭСП тоже в
раз приведет к уменьшению напряженности ЭСП тоже в 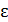 раз, так как эти величины пропорциональны друг другу.
раз, так как эти величины пропорциональны друг другу.
5) Сравним энергии ЭСП: так как заряд обкладок 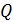 не изменяется, то используем следующую формулу:
не изменяется, то используем следующую формулу:
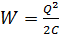 . (4)
. (4)
В этом случае отношение энергий
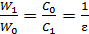 .
.
Следовательно, энергия электрического поля конденсатора уменьшилась в 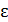 раз.
раз.
б) Пластина диэлектрика вдвигается в конденсатор, подсоединенный к источнику тока (рис. 37 б).
2) Напряжение на конденсаторе равно ЭДС источника тока: 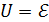 , – так как каждый проводник, соединяющий источник тока с обкладкой конденсатора, в условиях электростатики эквипотенциален. Таким образом,
, – так как каждый проводник, соединяющий источник тока с обкладкой конденсатора, в условиях электростатики эквипотенциален. Таким образом, 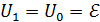 и отношение
и отношение 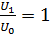 .
.
3) Электроемкость зависит только от геометрических параметров (размеров и формы обкладок) конденсатора и от диэлектрической проницаемости диэлектрика 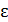 , и не зависит ни от заряда конденсатора, ни от разности потенциалов между обкладками. Поэтому, в соответствии с формулой (1), так же, как и в случае «а», емкость конденсатора при помещении пластины диэлектрика увеличится в
, и не зависит ни от заряда конденсатора, ни от разности потенциалов между обкладками. Поэтому, в соответствии с формулой (1), так же, как и в случае «а», емкость конденсатора при помещении пластины диэлектрика увеличится в 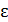 раз.
раз.
1) В соответствии с формулой 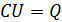 , увеличение емкости конденсатора
, увеличение емкости конденсатора 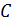 в
в 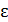 раз при неизменном напряжении
раз при неизменном напряжении 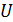 приведет к увеличению заряда обкладок также в
приведет к увеличению заряда обкладок также в 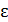 раз. Необходимые для этого дополнительные заряды придут на обкладки конденсатора с полюсов источника тока.
раз. Необходимые для этого дополнительные заряды придут на обкладки конденсатора с полюсов источника тока.
4) В соответствии с формулой (3), при неизменном напряжении 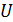 останется прежней и напряженность электрического поля конденсатора:
останется прежней и напряженность электрического поля конденсатора: 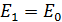 .
.
5) Значения энергии ЭСП сравним, используя формулу 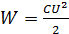 , так как напряжения на обкладках одинаковы:
, так как напряжения на обкладках одинаковы:  Согласно записанной формуле
Согласно записанной формуле
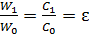 ,
,
т. е. энергия электрического поля конденсатора увеличилась в 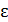 раз.
раз.
ЧАСТЬ 2
Дата: 2018-11-18, просмотров: 798.