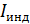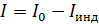Основной закон электромагнитной индукции (ЭМИ) – закон Фарадея: электродвижущая сила индукции 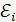 равна скорости изменения магнитного потока сквозь площадь контура:
равна скорости изменения магнитного потока сквозь площадь контура:
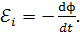 (24)
(24)
В каждом витке обмотки соленоида или тороида возникает ЭДС индукции, равная 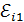 ; так как витки одинаковы и соединены последовательно, то ЭДС индукции, возникающая в катушке, равна сумме ЭДС
; так как витки одинаковы и соединены последовательно, то ЭДС индукции, возникающая в катушке, равна сумме ЭДС 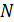 витков:
витков:
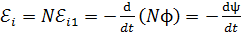 , (25)
, (25)
где 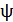 – потокосцепление контура.
– потокосцепление контура.
Частные случаи применения закона электромагнитной индукции (25):
1) при поступательном движении проводника длиной 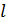
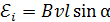 , (26)
, (26)
где 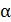 – угол между векторами скорости проводника
– угол между векторами скорости проводника 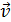 и магнитной индукции
и магнитной индукции  ;
;
2) при вращении рамки в однородном МП с индукцией 
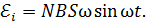 (27)
(27)
Здесь 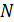 – число витков рамки;
– число витков рамки; 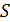 – площадь витка;
– площадь витка; 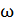 – угловая скорость вращения;
– угловая скорость вращения; 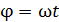 – угол поворота нормали рамки
– угол поворота нормали рамки 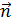 в момент времени
в момент времени 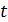 (при
(при 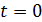 вектор
вектор 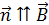 ).
).
Количество электричества 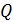 , протекающее через сечение проводника сопротивлением
, протекающее через сечение проводника сопротивлением 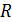 при изменении потокосцепления
при изменении потокосцепления 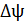 , определяется формулой
, определяется формулой
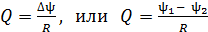 , (28)
, (28)
где 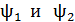 – потокосцепления контура в начальном и конечном положениях.
– потокосцепления контура в начальном и конечном положениях.
Заметим, что при решении задач контрольной работы №4 формулы (26), (27) и (28) следует выводить, исходя из основного закона ЭМИ (25).
Полный магнитный поток 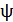 контура пропорционален току
контура пропорционален току 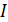 в этом контуре:
в этом контуре:
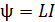 , (29)
, (29)
где 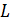 – коэффициент пропорциональности, называемый индуктивностью контура. Индуктивность длинного соленоида и тороида определяется формулой
– коэффициент пропорциональности, называемый индуктивностью контура. Индуктивность длинного соленоида и тороида определяется формулой
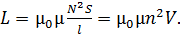 (30)
(30)
Здесь 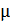 – магнитная проницаемость сердечника;
– магнитная проницаемость сердечника; 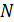 – число витков катушки;
– число витков катушки; 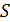 – площадь поперечного сечения сердечника (площадь витка);
– площадь поперечного сечения сердечника (площадь витка); 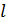 – длина сердечника;
– длина сердечника; 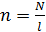 – число витков на единицу длины соленоида;
– число витков на единицу длины соленоида; 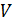 – объем сердечника.
– объем сердечника.
ЭДС самоиндукции 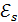 , возникающая в контуре при изменении в нем тока, в случае постоянной индуктивности контура
, возникающая в контуре при изменении в нем тока, в случае постоянной индуктивности контура 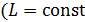 , если сердечник катушки неферромагнитный) изменяется по закону:
, если сердечник катушки неферромагнитный) изменяется по закону:
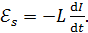 (31)
(31)
|
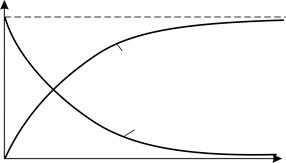
Рис. 56 |
|
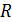 и индуктивность
и индуктивность 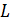 , ток изменяется с течением времени
, ток изменяется с течением времени 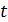 по следующему закону:
по следующему закону:
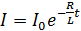 , (32)
, (32)
где 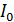 – ток в момент времени
– ток в момент времени 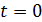 .
.
Ток, определяемый формулой (32), является индукционным; в соответствии с законом Ома, величина этого тока в любой момент времени 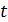 :
: 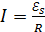 , где ЭДС самоиндукции
, где ЭДС самоиндукции 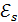 определяется законом ЭМИ (31).
определяется законом ЭМИ (31).
При подключении цепи к источнику тока ЭДС самоиндукции создает индукционный ток, препятствующий нарастанию тока до значения 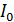 . В результате ток в цепи устанавливается с течением времени по закону
. В результате ток в цепи устанавливается с течением времени по закону
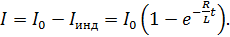 (33)
(33)
Здесь, согласно закону Ома, ток 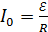 , где
, где 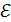 – ЭДС источника тока.
– ЭДС источника тока.
Энергия 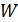 магнитного поля, которое создается током
магнитного поля, которое создается током 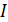 в контуре с индуктивностью
в контуре с индуктивностью 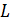 , вычисляется по следующей формуле:
, вычисляется по следующей формуле:
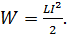 (34)
(34)
Объемная плотность энергии однородного МП 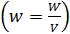 с магнитной индукцией
с магнитной индукцией  , например, в сердечнике длинного соленоида, определяется формулой
, например, в сердечнике длинного соленоида, определяется формулой
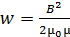 , (35)
, (35)
где 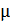 – магнитная проницаемость сердечника.
– магнитная проницаемость сердечника.
Магнитное поле в веществе
Вещество во внешнем магнитном поле с индукцией 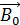 намагничивается и создает собственное МП с индукцией
намагничивается и создает собственное МП с индукцией 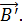 Результирующее магнитное поле является суперпозицией этих двух полей:
Результирующее магнитное поле является суперпозицией этих двух полей:
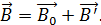 (36)
(36)
Индукция собственного магнитного поля магнетика
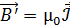 , (37)
, (37)
где 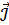 – намагниченность вещества, она равна сумме магнитных моментов молекул вещества, находящихся в единичном объеме магнетика (
– намагниченность вещества, она равна сумме магнитных моментов молекул вещества, находящихся в единичном объеме магнетика ( 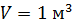 )
)
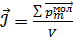 . (38)
. (38)
Величина намагниченности 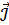 зависит от природы магнетика и напряженности МП
зависит от природы магнетика и напряженности МП 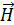 следующим образом:
следующим образом:
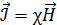 , (39)
, (39)
где 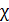 – магнитная восприимчивость вещества. С учетом этих соотношений принцип суперпозиции (36) запишем в следующем виде:
– магнитная восприимчивость вещества. С учетом этих соотношений принцип суперпозиции (36) запишем в следующем виде:
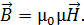 (40)
(40)
Здесь 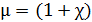 – магнитная проницаемость вещества.
– магнитная проницаемость вещества.
По соотношению индукции МП в вакууме и собственного магнитного поля различают 3 вида магнетиков:
1) диамагнетики (медь, графит, вода и др.): 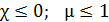 ;
;
2) парамагнетики (алюминий, платина и др.): 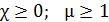 ;
;
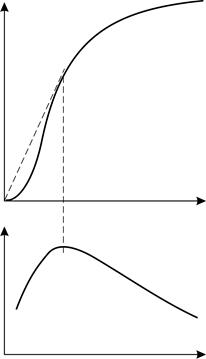
Рис. 57 |
диа- и парамагнетики относят к слабым магнетикам, так как их собственное поле мало: 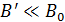 ;
;
3) ферромагнетики – сильные магнетики, так как их собственное поле 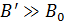 , а величина магнитной проницаемости
, а величина магнитной проницаемости 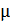 достигает
достигает 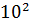 …
… 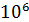 ; ферромагнетиками являются железо, кобальт, никель, их сплавы с другими металлами и др.
; ферромагнетиками являются железо, кобальт, никель, их сплавы с другими металлами и др.
Для ферромагнетиков характерна нелинейная кривая намагничивания: зависимость 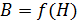 , показанная на рис. 57 а, и зависимость магнитной проницаемости
, показанная на рис. 57 а, и зависимость магнитной проницаемости 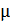 от напряженности магнитного поля:
от напряженности магнитного поля: 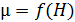 (рис. 57 б). Если ферромагнетик намагнитить до насыщения, а затем уменьшать напряженность
(рис. 57 б). Если ферромагнетик намагнитить до насыщения, а затем уменьшать напряженность 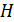 намагничивающего поля, то кривая
намагничивающего поля, то кривая 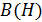 пойдет выше и при
пойдет выше и при 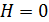 будет величина
будет величина 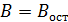 : остаточная намагниченность.
: остаточная намагниченность.
РЕКОМЕНДАЦИИ К РЕШЕНИЮ ЗАДАЧ ПО РАЗДЕЛУ
«ЭЛЕКТОМАГНЕТИЗМ»
1. Внимательно прочитайте условие задачи. Выясните, какое явление рассматривается в задаче, и изучите сведения о нем и о физических величинах, его описывающих, по разделу «7. Теоретическая часть».
2. При определении магнитных сил, магнитного потока и других величин обратите внимание на то, какое магнитное поле рассматривается в задаче – однородное или неоднородное. В первом случае используйте более простые формулы для однородного МП.
3. При решении задачи определяйте направления искомых векторов 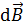 ,
, 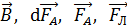 и др. Для этого используйте а) определительные формулы, в правой части которых записано векторное произведение векторов или б) правило буравчика (см. п. 7.1) и правило левой руки.
и др. Для этого используйте а) определительные формулы, в правой части которых записано векторное произведение векторов или б) правило буравчика (см. п. 7.1) и правило левой руки.
4. В том случае, если магнитное поле создается в ферромагнетике, для которого магнитная проницаемость 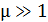 (в отличие от картонного или воздушного сердечника, имеющего
(в отличие от картонного или воздушного сердечника, имеющего 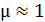 ), необходимо определять величину
), необходимо определять величину 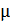 по формуле, связывающей напряженность
по формуле, связывающей напряженность 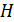 и магнитную индукцию
и магнитную индукцию  :
:
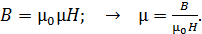 (41)
(41)
При этом следует учесть, что величина магнитной индукции зависит от напряженности МП: 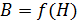 , – и соответственно
, – и соответственно 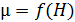 . Поэтому сначала вычисляют напряженность магнитного поля
. Поэтому сначала вычисляют напряженность магнитного поля 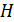 , которая зависит только от тока в контуре и формы и размеров контура (катушки). Затем по экспериментальному графику кривой намагничивания
, которая зависит только от тока в контуре и формы и размеров контура (катушки). Затем по экспериментальному графику кривой намагничивания 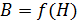 для заданного материала сердечника (используя справочные данные) по рассчитанной величине
для заданного материала сердечника (используя справочные данные) по рассчитанной величине 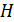 определяют индукцию магнитного поля
определяют индукцию магнитного поля  . По найденным значениям
. По найденным значениям 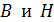 вычисляют магнитную проницаемость сердечника
вычисляют магнитную проницаемость сердечника 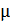 по формуле (41).
по формуле (41).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Дата: 2018-11-18, просмотров: 722.