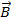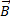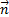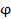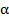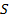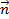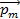В магнитном поле
План решения задач
1. При вычислении магнитного потока 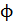 следует обращать внимание на характер магнитного поля. В случае однородного поля величина магнитного потока определяется простой формулой:
следует обращать внимание на характер магнитного поля. В случае однородного поля величина магнитного потока определяется простой формулой:
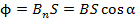 ,
,
где 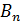 – проекция вектора магнитной индукции
– проекция вектора магнитной индукции  на нормаль
на нормаль 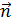 к плоскости контура площадью
к плоскости контура площадью 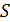 ;
; 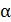 – угол между векторами
– угол между векторами 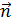 и
и  .
.
Для неоднородного поля необходимо вычислять интеграл:
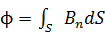 .
.
2. В условии задачи нередко задают угол 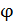 между вектором магнитной
между вектором магнитной

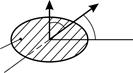
Рис. 74 |
индукции  и плоскостью контура (рис. 74). В таком случае необходим рисунок (см. рис. 74), по которому видно, что угол
и плоскостью контура (рис. 74). В таком случае необходим рисунок (см. рис. 74), по которому видно, что угол  ; тогда
; тогда
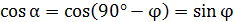 .
.
3. Расчет работы по перемещению проводника или контура с током в магнитном поле, независимо от того, движется проводник поступательно (работа силы Ампера 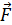 ) или происходит поворот контура (работа механического момента сил Ампера), наиболее просто выполняется с помощью следующей формулы:
) или происходит поворот контура (работа механического момента сил Ампера), наиболее просто выполняется с помощью следующей формулы:
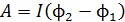 ,
,
где 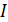 – ток в контуре;
– ток в контуре; 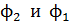 – магнитный поток сквозь поверхность, ограниченную контуром, в конечном (индекс 2) и в начальном (индекс 1) положениях контура, соответственно. Отметим, что работа сил Ампера положительна. Если при вычислении получена отрицательная величина, то это означает, что работу по заданному перемещению осуществляют внешние силы
– магнитный поток сквозь поверхность, ограниченную контуром, в конечном (индекс 2) и в начальном (индекс 1) положениях контура, соответственно. Отметим, что работа сил Ампера положительна. Если при вычислении получена отрицательная величина, то это означает, что работу по заданному перемещению осуществляют внешние силы 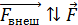 , а модуль
, а модуль 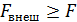 , где
, где 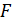 – сила Ампера.
– сила Ампера.
4. Заметим, что единица измерения магнитного потока 1 Вб 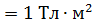 , – весьма большая величина. Поэтому в обычных полях с магнитной индукцией
, – весьма большая величина. Поэтому в обычных полях с магнитной индукцией  порядка 1 мТл магнитный поток
порядка 1 мТл магнитный поток 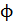 через поверхность контуров небольших размеров площадью
через поверхность контуров небольших размеров площадью 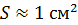 по порядку величины не превышает
по порядку величины не превышает 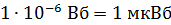 .
.
Задача 43. Обмотка соленоида с током 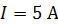 содержит
содержит 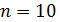 витков на каждый сантиметр длины. В средней части соленоида помещен круговой контур радиусом
витков на каждый сантиметр длины. В средней части соленоида помещен круговой контур радиусом 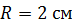 . Плоскость контура расположена под углом
. Плоскость контура расположена под углом 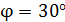 к оси соленоида. Определите магнитный поток
к оси соленоида. Определите магнитный поток 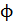 , пронизывающий контур.
, пронизывающий контур.
Дано Решение
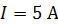 ; ;
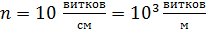 ; ;
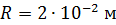 ; ;
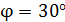 . .
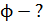
|

Рис. 75 |
Линии магнитного поля внутри соленоида параллельны его оси (рис. 75). В средней части соленоида, удаленной от его торцов, индукция магнитного поля определяется по формуле:
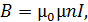 (1)
(1)
где 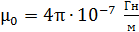 – магнитная постоянная,
– магнитная постоянная, 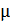 – магнитная проницаемость сердечника (для воздуха
– магнитная проницаемость сердечника (для воздуха 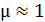 );
); 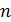 – число витков на единицу длины соленоида;
– число витков на единицу длины соленоида; 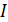 – сила тока в обмотке соленоида. Величина
– сила тока в обмотке соленоида. Величина  одинакова в сечении соленоида, т. е. его магнитное поле является однородным.
одинакова в сечении соленоида, т. е. его магнитное поле является однородным.
Магнитный поток 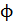 через площадь контура в однородном магнитном поле определим по следующей формуле:
через площадь контура в однородном магнитном поле определим по следующей формуле:
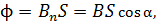 (2)
(2)
где 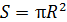 – площадь, ограниченная контуром;
– площадь, ограниченная контуром; 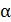 – угол между нормалью
– угол между нормалью 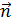 к плоскости контура и вектором магнитной индукции
к плоскости контура и вектором магнитной индукции  . По рисунку (см. рис. 75) видно, что угол
. По рисунку (см. рис. 75) видно, что угол 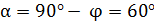 .
.
Подставляя в формулу (2) величины магнитной индукции  и площади
и площади 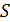 , получаем расчетную формулу в следующем виде:
, получаем расчетную формулу в следующем виде:
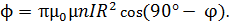 (3)
(3)
Вычисляем магнитный поток 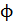 , пронизывающий контур, помещенный внутри данного соленоида:
, пронизывающий контур, помещенный внутри данного соленоида:
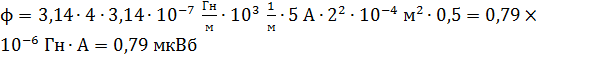 .
.
Задача 44. Магнитный момент длинного соленоида 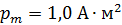 , длина соленоида
, длина соленоида 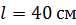 . Определите магнитный поток
. Определите магнитный поток 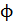 сквозь сечение сердечника соленоида.
сквозь сечение сердечника соленоида.
Дано Решение
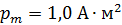 ; ;
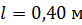 . .
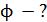
|
|
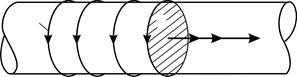
Рис.76 |
Магнитный поток через сечение площадью 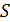 в однородном магнитном поле соленоида определяется формулой
в однородном магнитном поле соленоида определяется формулой
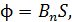 (1)
(1)
где 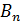 – проекция вектора магнитной индукции
– проекция вектора магнитной индукции  на нормаль
на нормаль 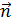 к площади поперечного сечения сердечника соленоида (рис. 76);
к площади поперечного сечения сердечника соленоида (рис. 76); 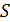 – площадь этого сечения, равная площади витка обмотки соленоида.
– площадь этого сечения, равная площади витка обмотки соленоида.
Вектор магнитной индукции поля внутри соленоида параллелен его оси, следовательно, проекция вектора  , где величина индукции магнитного поля в средней части соленоида определяется по следующей формуле:
, где величина индукции магнитного поля в средней части соленоида определяется по следующей формуле:
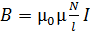 . (2)
. (2)
Здесь 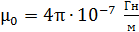 – магнитная постоянная,
– магнитная постоянная, 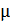 – магнитная проницаемость сердечника, для воздуха
– магнитная проницаемость сердечника, для воздуха 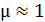 ;
; 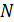 – число витков соленоида;
– число витков соленоида; 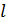 – его длина;
– его длина; 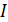 – сила тока в обмотке соленоида.
– сила тока в обмотке соленоида.
Подставляя величину магнитной индукции  в формулу (1), находим магнитный поток в сечении соленоида
в формулу (1), находим магнитный поток в сечении соленоида
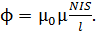 (3)
(3)
Магнитный момент соленоида 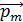 – это вектор, равный сумме магнитных моментов
– это вектор, равный сумме магнитных моментов  всех
всех 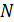 витков соленоида:
витков соленоида:
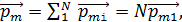 (4)
(4)
где 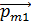 – магнитный момент одного витка обмотки; здесь сумму одинаковых слагаемых
– магнитный момент одного витка обмотки; здесь сумму одинаковых слагаемых  заменили произведением. Так как модуль
заменили произведением. Так как модуль 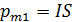 , то магнитный момент соленоида, в соответствии с формулой (4):
, то магнитный момент соленоида, в соответствии с формулой (4):
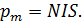 (5)
(5)
Сравнивая формулы (5) и (3), отметим, что магнитный поток соленоида пропорционален величине 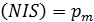 , следовательно, формулу (3) можно записать в следующем виде:
, следовательно, формулу (3) можно записать в следующем виде:
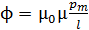 .
.
По этой формуле вычисляем магнитный поток сквозь сечение заданного соленоида:
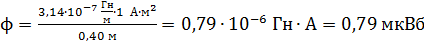 .
.
Задача 45. Круговой контур (виток) радиусом 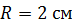 , в котором поддерживается постоянный ток
, в котором поддерживается постоянный ток 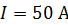 , свободно установился в однородном магнитном поле с индукцией
, свободно установился в однородном магнитном поле с индукцией 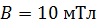 . Какую работу нужно совершить для того, чтобы 1) повернуть виток относительно оси, совпадающей с диаметром, на угол
. Какую работу нужно совершить для того, чтобы 1) повернуть виток относительно оси, совпадающей с диаметром, на угол 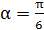 ; 2) удалить виток в область, где магнитное поле отсутствует.
; 2) удалить виток в область, где магнитное поле отсутствует.
Дано Решение
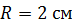 ; ;
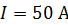 ; ;
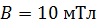 . .
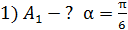 ;
2) ;
2) 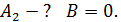
|
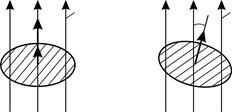
а б Рис. 77 |
Виток с током, который свободно установился в магнитном поле, находится в состоянии устойчивого равновесия. При этом механический момент 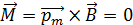 , поэтому магнитный момент контура
, поэтому магнитный момент контура  , чтобы
, чтобы 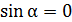 . Магнитный момент
. Магнитный момент 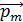 сонаправлен с нормалью
сонаправлен с нормалью 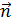 к плоскости контура, следовательно, нормаль
к плоскости контура, следовательно, нормаль 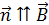 (рис. 77 а).
(рис. 77 а).
В этом начальном положении магнитный поток через площадь, ограниченную контуром, максимален и равен
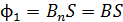 , (1)
, (1)
так как 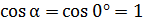 и проекция вектора магнитной индукции
и проекция вектора магнитной индукции  .
.
1) При повороте плоскости контура на угол 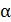 и нормаль к этой плоскости повернется на угол
и нормаль к этой плоскости повернется на угол 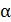 (рис. 77 б). Магнитный поток при этом уменьшится и в новом положении контура станет равным
(рис. 77 б). Магнитный поток при этом уменьшится и в новом положении контура станет равным
 (2)
(2)
Работу, совершаемую при повороте контура, определим по формуле:
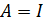 (
( 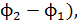 (3)
(3)
где 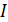 – ток в контуре;
– ток в контуре; 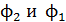 – магнитные потоки сквозь поверхность, ограниченную контуром, соответственно, в конечном (индекс 2) и в начальном (индекс 1) положениях контура. Подставляя значения
– магнитные потоки сквозь поверхность, ограниченную контуром, соответственно, в конечном (индекс 2) и в начальном (индекс 1) положениях контура. Подставляя значения 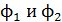 по формулам (1) и (2), в которых площадь кругового контура
по формулам (1) и (2), в которых площадь кругового контура 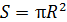 , получаем следующую расчетную формулу для величины работы:
, получаем следующую расчетную формулу для величины работы:
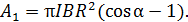 (4)
(4)
Вычисляем величину работы, которая совершается при повороте контура:
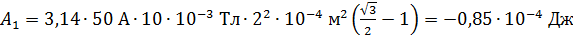 .
.
2) После удаления контура с током в область, где индукция магнитного поля 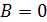 , магнитный поток
, магнитный поток 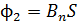 станет нулевым. Соответственно, работа, определяемая также формулой (3), запишется в следующем виде:
станет нулевым. Соответственно, работа, определяемая также формулой (3), запишется в следующем виде:
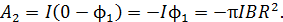
Вычислим эту работу, совершаемую при удалении контура с током в область, где магнитное поле отсутствует:
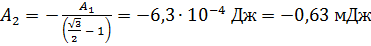 .
.
Работа, совершаемая при перемещении контура, в обоих случаях отрицательная. Это означает, что работу совершает внешняя сила 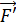 , направленная противоположно силе Ампера (в случае
, направленная противоположно силе Ампера (в случае 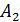 ); а в первом случае – при повороте контура, работу совершает момент внешней силы
); а в первом случае – при повороте контура, работу совершает момент внешней силы 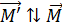 , который создается магнитными силами.
, который создается магнитными силами.
Задача 46. В одной плоскости с длинным прямым проводником с током 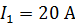 расположена квадратная рамка со стороной
расположена квадратная рамка со стороной 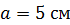 так, что расстояние от провода до ближайшей стороны рамки
так, что расстояние от провода до ближайшей стороны рамки 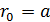 (рис. 78). В рамке течет ток
(рис. 78). В рамке течет ток  . Определите работу, которую нужно совершить для медленного поворота рамки относительно оси
. Определите работу, которую нужно совершить для медленного поворота рамки относительно оси 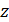 на угол
на угол 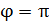 .
.
Дано Решение
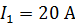 ; ;
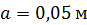 ; ;
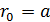 ; ;
 ; ;
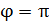 . .
|
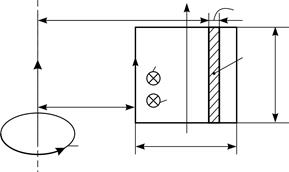
Рис. 78 |
При медленном повороте рамки скорость изменения магнитного потока 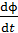 мала, поэтому величиной ЭДС индукции и возникающим в рамке индукционным током можно пренебречь и считать постоянной величину тока в рамке:
мала, поэтому величиной ЭДС индукции и возникающим в рамке индукционным током можно пренебречь и считать постоянной величину тока в рамке: 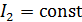 . В таком случае работа при повороте контура описывается формулой
. В таком случае работа при повороте контура описывается формулой
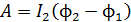 , (1)
, (1)
где 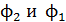 – магнитный поток через площадь, ограниченную рамкой, в конечном и начальном положениях рамки.
– магнитный поток через площадь, ограниченную рамкой, в конечном и начальном положениях рамки.
Магнитный поток через площадь рамки создается магнитным полем длинного проводника с током 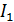 . Магнитная индукция этого поля в точках на расстоянии
. Магнитная индукция этого поля в точках на расстоянии 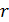 от провода определяется следующей формулой:
от провода определяется следующей формулой:
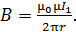 (2)
(2)
По этой формуле видно, что величина  уменьшатся по мере увеличения расстояния
уменьшатся по мере увеличения расстояния 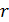 от провода, следовательно, магнитное поле, в котором находится рамка, является неоднородным. Линии магнитной индукции
от провода, следовательно, магнитное поле, в котором находится рамка, является неоднородным. Линии магнитной индукции  – окружности, охватывающие длинный проводник, они перпендикулярны плоскости рамки и вектор
– окружности, охватывающие длинный проводник, они перпендикулярны плоскости рамки и вектор  направлен «от нас». Нормаль
направлен «от нас». Нормаль 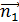 к плоскости рамки, как принято, связана правилом буравчика с током
к плоскости рамки, как принято, связана правилом буравчика с током 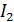 в рамке и также направлена «от нас» (см. рис. 78). В этом случае проекция вектора
в рамке и также направлена «от нас» (см. рис. 78). В этом случае проекция вектора  на нормаль
на нормаль 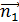 положительна и равна модулю вектора
положительна и равна модулю вектора  :
:
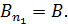 (3)
(3)
Для вычисления магнитного потока 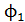 в начальном положении рамки отметим, что в неоднородном магнитном поле величину
в начальном положении рамки отметим, что в неоднородном магнитном поле величину 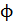 находят как сумму элементарных потоков
находят как сумму элементарных потоков 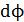 через бесконечно малые площадки
через бесконечно малые площадки 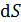 :
:
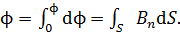 (4)
(4)
Элементарные площадки 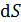 выберем в форме узких полосок ширины
выберем в форме узких полосок ширины 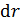 и площадью
и площадью 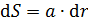 , параллельных длинному проводнику и находящихся от него на расстоянии, равном
, параллельных длинному проводнику и находящихся от него на расстоянии, равном 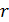 (см. рис. 78). В пределах такой полоски величину
(см. рис. 78). В пределах такой полоски величину  , определяемую формулой (2), можно считать одинаковой. Подставляя значение проекции
, определяемую формулой (2), можно считать одинаковой. Подставляя значение проекции 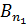 с учетом формулы (2) в выражение (4), рассчитаем магнитный поток в начальном положении рамки следующим образом:
с учетом формулы (2) в выражение (4), рассчитаем магнитный поток в начальном положении рамки следующим образом:
 (5)
(5)
Здесь пределы интегрирования по переменной 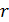 взяты соответственно
взяты соответственно 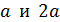 , чтобы охватить всю площадь рамки, по которой суммируются элементарные магнитные потоки
, чтобы охватить всю площадь рамки, по которой суммируются элементарные магнитные потоки 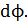
После поворота плоскости рамки относительно оси 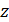 на угол
на угол 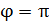 рамка вновь будет расположена в плоскости рисунка, но только вектор нормали к плоскости рамки, повернувшись также на угол, равный
рамка вновь будет расположена в плоскости рисунка, но только вектор нормали к плоскости рамки, повернувшись также на угол, равный 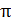 , будет направлен «к нам», т. е. нормаль
, будет направлен «к нам», т. е. нормаль 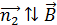 . В таком положении рамки проекция вектора
. В таком положении рамки проекция вектора  на нормаль отрицательна:
на нормаль отрицательна:
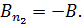 (6)
(6)
Соответственно, магнитный поток в конечном положении рамки, определяемый интегралами (4)и (5), будет отличаться от величины 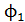 только знаком:
только знаком:
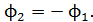 (7)
(7)
С учетом выражений (5) и (7) формула (1) для вычисления работы преобразуется к следующему виду:
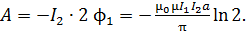 (8)
(8)
Вычисляем величину работы при повороте рамки по расчетной формуле (8), принимая для воздуха магнитную проницаемость 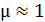 :
:
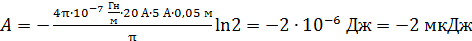 .
.
Величина работы отрицательна, так как поворот совершается моментом внешних сил, поворачивающим рамку из положения устойчивого равновесия: в начальном положении рамки ее магнитный момент 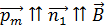 .
.
Дата: 2018-11-18, просмотров: 690.